ملاحظات الصيغة:< /strong>Due الخوارزمية المستندة إلى SHA 256 عبارة عن سلسلة مكونة من 256 بت، لذلك يوجد 2^256 (هنا "^" تعني الطاقة) أقصى عدد من التجزئات. إذا كنت تريد العثور على حل فعال أكبر من d، فهناك هي فقط 2 ^256-d عدد التجزئة، والتي يمكن من خلالها حساب احتمالية النجاح في محاولة واحدة. إذا كان لدى أليس n من النسخ المتماثلة ويمكن لكل نسخة متماثلة إجراء k من المحاولات في الثانية، فإنها تجد الحل في أي ثانية معينة والاحتمال هو:
< p>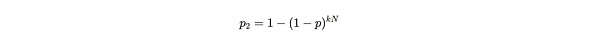
ملاحظات الصيغة:kN تعني إجمالي عدد محاولات حل التجزئة التي يمكن لـ Alice إجراؤها في ثانية واحدة. ويتناسب عدد المحاولات هذا مع عدد النسخ الفريدة المخزنة بواسطة Alice. للحصول على شرح محدد، يمكنك قراءة محتوى المقالة السابقة "Arweave 2.6 قد يكون أكثر انسجاما مع رؤية ساتوشي ناكاموتو". 1-p هو احتمال الفشل في محاولة واحدة. قيمة احتمالية p2 هي 1 مطروحًا منها احتمالية الفشل في محاولات kN.
من خلال استبدال واشتقاق الصيغتين أعلاه يمكننا الحصول على:

ملاحظات الصيغة: استبدل p في النتائج التي تم الحصول عليها من صيغة P2
يمكن محاكاة الوقت اللازم لأليس لتقديم الدليل بواسطة متغير عشوائي هندسي X ~ Geom(p2) ، p2 هو احتمال النجاح. هذا المتغير العشوائي X يعتمد على d و k و n . من أجل التحقق مما إذا كانت أليس تكذب أم لا، يرسل بوب صعوبة d حتى تتمكن أليس من تقديم دليل إلى بوب كل 120 ثانية بعدد n من النسخ. وهذا يعادل احتمالية نجاح أليس خلال 120 ثانية:
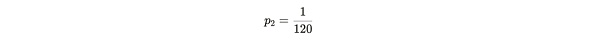
ملاحظات الصيغة:1/120 هو احتمال إرسال إثبات بنجاح خلال 120 ثانية
إذا تمكنت أليس من إرسال الدليل خلال الوقت المطلوب، فمن المحتمل أن يكون لديها العدد الصحيح من النسخ الفريدة. ولكن دليلاً واحداً لا يكفي لإقناع بوب بأن أليس لا تكذب. فإذا تمكنت أليس من تقديم البراهين كل 120 ثانية في المتوسط على مدى فترة طويلة من الزمن، فمن الممكن أن يكون بوب واثقاً إلى حد معقول من أن أليس قامت بتخزين الكمية المتوقعة من البيانات.
بعد ذلك نحاول قياس مدى يقين تخزين بوب لأليس.
لنفترض أن أليس تطالب بتخزين 20 نسخة متماثلة وتقدم البراهين بشكل متسق بمعدل 120 ثانية خلال فترة أسبوعين (إثبات إجمالي 10,080 إرسالًا). في هذه المرحلة، يتساءل بوب عن احتمالية استمرار أليس في تقديم هذه البراهين إذا قامت بتخزين 19 نسخة متماثلة (أو أقل) فقط. يتوافق هذا مع احتمال تقديم دليل في ثانية مختلفة:
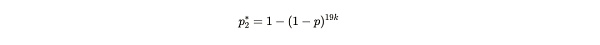
تعليق الصيغة: ظهور 19k هنا يعني أن Alice قد حفظت 19 نسخة، وكل نسخة بها k من المحاولات للعثور على حل. عدد الخطط.
التبسيط المفرط:

يمكن حساب هذا الاحتمال باستخدام قيمة d التي أنشأها بوب لأليس الصادقة. إذا قامت بتخزين 19 نسخة أو أقل، فإن احتمال تقديم الدليل في ثانية واحدة يمكن العثور عليه من خلال سلسلة من الاشتقاقات الواردة أدناه. من بينها، يمثل p2 احتمال إنشاء دليل خلال ثانية واحدة عندما تقوم أليس بتخزين 20 نسخة بأمانة، بينما يمثل p2* احتمال تقديم دليل خلال ثانية واحدة إذا كانت تكذب (مخزنة ≥ 19 نسخة):
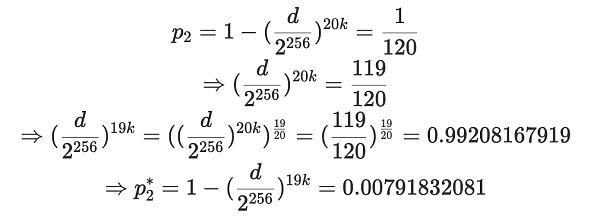
قد تبدو عملية الاشتقاق هذه معقدة، ولكن في الواقع، يمكن لأي شخص يتمتع بقدرات رياضية أساسية أن يفهمها. عملية الاشتقاق هي عملية استبدال الشركات المذكورة أعلاه.
وهكذا، p2*=0.00791832081، يتوافق مع الوقت المتوقع لإنشاء البرهان وهو 126.2894 ثانية. اجعل X* هو الوقت الذي قدمت فيه Alice الدليل الذي تم الحصول عليه من p2*، أي X*~ Geom(p2*). يمثل هذا الموقف الذي تكذب فيه أليس - حيث يتم تخزين 19 نسخة فقط، والقيمة المتوقعة (المتوسطة) للوقت الذي يستغرقه إرسال الدليل X* هي:

ملاحظات الصيغة:E[ X*] يعني أن متوسط الوقت الذي تستغرقه أليس لإرسال الدليل بنجاح هو 126.2894 ثانية على افتراض أنه تم تخزين 19 نسخة فقط. إذا قامت بتخزين 20 نسخة، فإن متوسط وقت الالتزام الناجح هو 120 ثانية. يمكننا استخدام نظرية الحد المركزي لتقدير احتمال أن يكون متوسط العينة أقل من 120، وهو ما يختلف عن القيمة المتوقعة E[X*] التي تم الحصول عليها فوق. يتم التعبير عن هذا الاحتمال على النحو التالي:
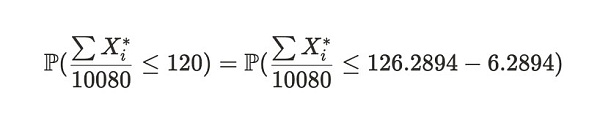
التعليقات التوضيحية للصيغة: يمثل التعبير الموجود على الجانب الأيسر من المعادلة احتمال أنه خلال أسبوعين، يكون متوسط وقت إرسال أليس لكل دليل أقل من أو يساوي 120 ثواني. الجانب الأيمن من المعادلة هو شكل مختلف من التعبير الموجود على اليسار.
بالنسبة لعدد كبير من العينات، يميل الجانب الأيسر من هذه المتراجحة إلى التوزيع الطبيعي بمتوسط E[X*] وتباين σX*^2/n ، حيث σX* هو الانحراف المعياري لـ Xd وn (هنا = 10,080) هو حجم العينة. لذلك، يمكن أن تصبح الصيغة أعلاه:
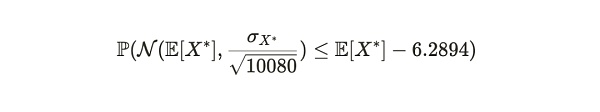
يمكننا تحويل هذا التوزيع إلى النموذج العادي القياسي للحصول على احتمالات مكافئة:

أخيرًا، باستخدام جدول التوزيع الطبيعي القياسي، يمكننا الحصول على احتمال كذب أليس في هذا الفترة الزمنية للأسبوع:
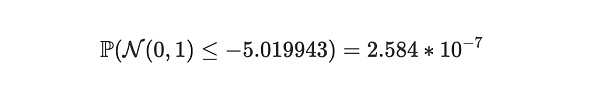
لذا، في هذا المثال، يستطيع بوب أن يحدد بنسبة يقين تبلغ 99.99997416% تقريبًا أن أليس قامت بتخزين أكثر من 19 نسخة من مجموعة البيانات خلال الأسبوعين. نلاحظ أنه إذا قامت أليس بتخزين أقل من 19 نسخة متماثلة، فسيكون الوقت المتوقع لتقديم الإثبات أكبر من 126.3 ثانية. نلاحظ أيضًا أن نظام الإثبات بأكمله يتطلب فقط إرسال إثبات كل 120 ثانية. هذا هو متوسط معدل نقل البيانات بين أليس وبوب يبلغ 2.389 كيلو بايت في الثانية (280 كيلو بايت/120 ثانية)، وهو ما يمكن مقارنته بحمل المزامنة لشبكة بيتكوين.
أخيرًا، لا تتغير هذه الاحتمالات مع الزيادات العشوائية في حجم مجموعة البيانات، ولكن زيادة فترة أخذ العينات ستستمر في تحسين نسخة بوب من أليس بخطية فائقة معدل اليقين الكمي للدقة (الشكل 1).
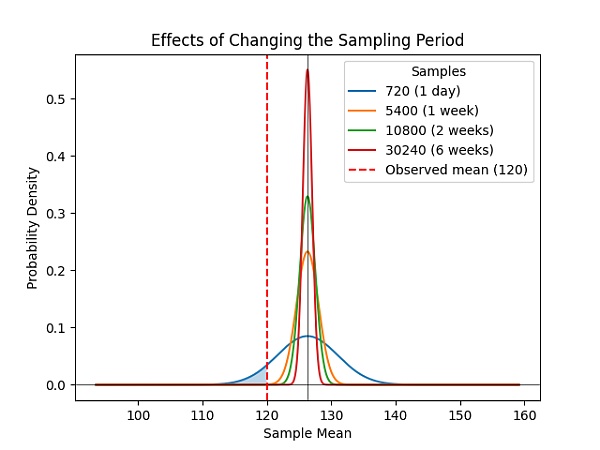
الشكل 1: في لعبة Succinct Proof of Replication (SPoRes)، يزداد اليقين بشكل خطي فائق مع مدة العينة. بعد أسبوعين من جمع العينات، كان احتمال الاحتفاظ بأقل من 19 نسخة متماثلة ضئيلًا (P<0.0000002584).
لذلك، يتم تعريف لعبة SPoRes من خلال المعلمات التالية:
أين:
r= جذر Merkle لمجموعة البيانات المستخدمة في اللعبة.
k= الحد الأقصى لعدد التحديات التي يتم فتحها في الثانية لكل نسخة.
d= معلمة الصعوبة التي تحدد احتمالية النجاح في كل محاولة.
من خلال هذه الاشتقاقات الرياضية المثيرة للاهتمام، يمكننا أن نقرر بأمان أنه يمكن تحديدها طالما استمر القائمون بالتعدين في تقديم البراهين خلال فترة زمنية معقولة ما إذا كان يتم تخزين البيانات. يشكل هذا جوهر آلية إجماع Arweave التي تستهدف التخزين اللامركزي. لقد بدأت متعة الرياضيات للتو، وسيكون هناك المزيد من الاستنتاجات والحجج المثيرة للاهتمام في المقالات التالية.
رابط الاقتباس
1. تويتر Arweave Eco:
https://twitter.com/@ArweaveEco
2. #SPoA:
https://twitter.com/search?q=%23SPoA&src= hashtag_click
3.#SPoRes:
https:/ /twitter.com/search?q=%23SPoRes&src=hashtag_click
4. الرابط الأصلي:
https://twitter.com/ArweaveOasis/status/1772089247660638417
 JinseFinance
JinseFinance
 JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance Others
Others Cointelegraph
Cointelegraph