Advanced Formal Verification of Zero-Knowledge Proofs: How to Verify a ZK Instruction

Source: CertiK Chinese Community

In order to deeply understand how formal verification technology is applied to zkVM (zero-knowledge virtual machine), this article will focus on the verification of a single instruction. For an overview of advanced formal verification of ZKP (zero-knowledge proof), please refer to our "Advanced Formal Verification of Zero-Knowledge Proof Blockchain" article published at the same time.

What is the verification of ZK instructions?

zkVM (zero-knowledge virtual machine) can create short proof objects as evidence to prove that a specific program can run on certain inputs and successfully terminate. In the field of Web3.0, the application of zkVM enables high throughput because L1 nodes only need to verify a short proof of the process of the smart contract from the input state to the output state, while the actual contract code execution can be completed off-chain.

The zkVM prover first runs the program to generate execution records for each step, and then converts the data of the execution record into a set of digital tables (a process called "arithmization"). These numbers must satisfy a set of constraints (i.e., circuits) that include equations connecting specific table cells, fixed constants, database lookup constraints between tables, and polynomial equations (i.e., "gates") that must be satisfied between each pair of adjacent table rows. On-chain verification can thus confirm that there is indeed a table that satisfies all the constraints, while ensuring that the specific numbers in the table cannot be seen.

Each VM instruction is subject to many of these constraints, and here we refer to the set of constraints for a VM instruction as its "ZK instruction." Below is an example of a zkWasm memory load instruction constraint written in Rust.

Formal verification of ZK instructions is accomplished by formal reasoning over these codes, which we first translate into a formal language.

Even if only a single constraint contains an error, it is possible for an attacker to submit a malicious ZK proof. The data table corresponding to the malicious proof does not correspond to the legal operation of the smart contract. Unlike non-ZK chains such as Ethereum, which have many nodes running different EVM (Ethereum Virtual Machine) implementations, making it unlikely that the same error will occur at the same time and place, a zkVM chain has only a single VM implementation. From this perspective alone, ZK chains are more vulnerable than traditional Web3.0 systems.

To make matters worse, unlike non-ZK chains, since the computation details of zkVM transactions are not submitted and stored on the chain, after an attack occurs, it is not only difficult to discover the specific details of the attack, but even identifying the attack itself becomes extremely challenging.

The zkVM system requires extremely rigorous scrutiny, and unfortunately, the correctness of the zkVM circuit is difficult to guarantee.

Why is it difficult to verify ZK instructions?

VM (virtual machine) is one of the most complex parts of the Web3.0 system architecture. The power of smart contracts is at the core of Web3.0's capabilities, and its power comes from the underlying VM, which is both flexible and complex: in order to complete general computing and storage tasks, these VMs must be able to support a large number of instructions and states. For example, the geth implementation of EVM requires more than 7,500 lines of Go language code. Similarly, the ZK circuits that constrain the execution of these instructions are equally large and complex. For example, in the zkWasm project, the implementation of the ZK circuit requires more than 6,000 lines of Rust code.

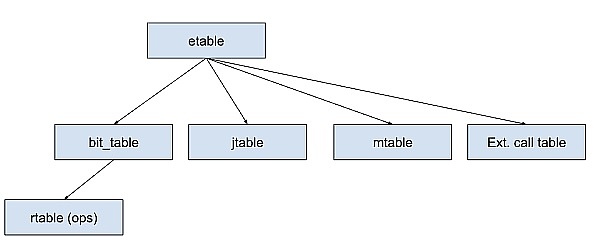
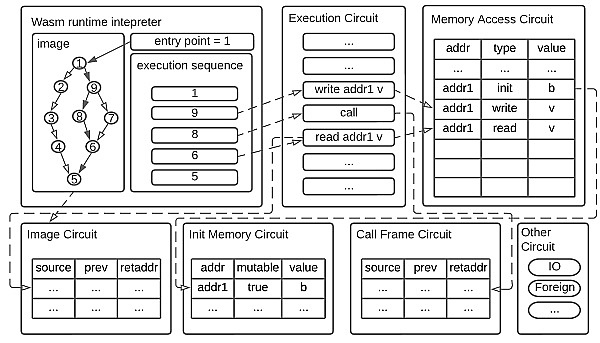zkWasm Circuit Architecture

Compared to dedicated ZK circuits used in ZK systems designed for specific applications (such as private payments), zkVM circuits are much larger in scale: the number of constraints may be one to two orders of magnitude larger than the former, and its arithmetic table may include hundreds of columns and contain millions of digital cells.

What does verification of ZK instructions mean?

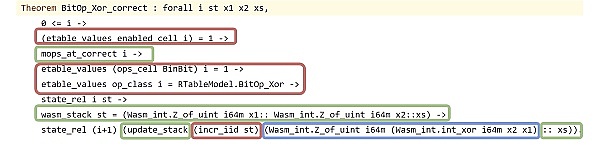
Here we want to verify the correctness of the XOR instruction in zkWasm. Technically, the execution table of zkWasm corresponds to a legal Wasm VM execution sequence. So at a macro level, what we want to verify is that each execution of this instruction always produces a new legal zkVM state: each row in the table corresponds to a legal state of the VM, and the next row is always generated by executing the corresponding VM instruction. The figure below is a formal theorem for the correctness of the XOR instruction.

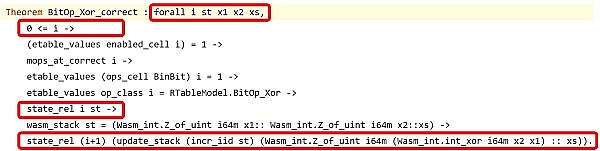
Here "state_rel i st" indicates that state "st" is a legal zkVM state of the smart contract in step "i". As you might guess, it is not trivial to prove that "state_rel (i+1) ...".

How to verify ZK instructions?

Although the computational semantics of the XOR instruction is simple, that is, to calculate the bitwise XOR of two integers and return the integer result, it involves more aspects: first, it needs to take out two integers from the stack memory, perform XOR calculation, and then store the new integer calculated back to the same stack. In addition, the execution steps of this instruction should be integrated into the execution process of the entire smart contract, and its execution order and timing must be correct.

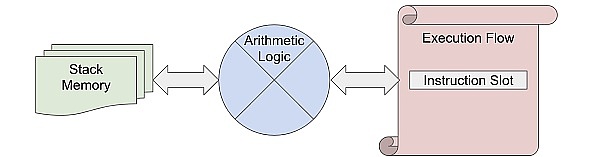
Therefore, the execution effect of the XOR instruction should be to pop two numbers from the data stack, push their XOR results, and increase the program counter to point to the next instruction of the smart contract.

It is not difficult to see that the definition of correctness properties here is generally very similar to what we face when verifying traditional bytecode VMs (such as the EVM interpreter in Ethereum L1 nodes). It relies on a high-level abstract definition of the machine state (here refers to stack memory and execution flow), as well as a definition of the expected behavior of each instruction (here refers to arithmetic logic).

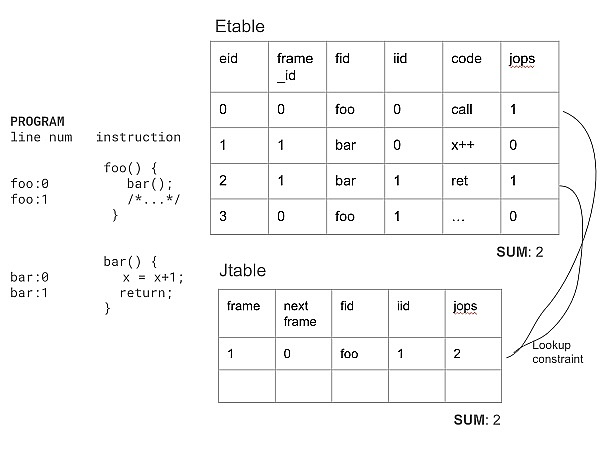
However, as we will see below, due to the particularity of ZKP and zkVM, the verification process of its correctness is often very different from that of conventional VMs. Just verifying our single instruction here depends on the correctness of many tables in zkWASM: there is a range table for limiting the size of values, a bit table for intermediate results of binary bit calculations, an execution table where each row stores a constant-sized VM state (similar to the data in registers and latches in a physical CPU), and memory tables and jump tables representing dynamically variable-sized VM states (memory, data stack, and call stack).

Step 1: Stack Memory

Similar to traditional VMs, we need to ensure that the two integer parameters of the instruction can be read from the stack and that their XOR result values ​​are correctly written back to the stack. The formal representation of the stack also looks quite familiar (there is also global memory and heap memory, but the XOR instruction does not use them).

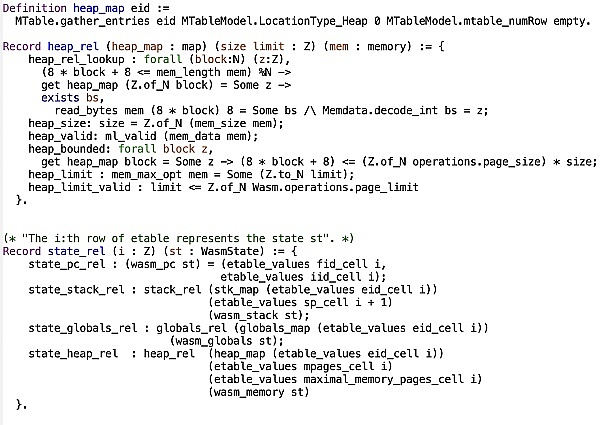
The zkVM uses a complex scheme to represent dynamic data, since the ZK prover does not natively support data structures like stacks or arrays. Instead, for each value pushed onto the stack, a memory table is recorded with a separate row, with some columns indicating when the entry is valid. Of course, the data in these tables can be controlled by an attacker, so some constraints must be imposed to ensure that the table entries correspond to actual push instructions in the contract execution. This is achieved by carefully counting the number of pushes during the execution of the program. When verifying each instruction, we need to ensure that this count is always correct. In addition, we have a series of lemmas that relate the constraints generated by a single instruction to the table lookup and time range checks that implement stack operations. At the top level, the counting constraints on memory operations are defined as follows.

Step 2: Arithmetic

Similar to traditional VMs, we want to make sure that the bitwise XOR operation is correct. This seems easy, after all, our physical computer CPU can complete this operation in one go.

But for zkVM, this is actually not that simple. The only two arithmetic instructions that the ZK prover natively supports are addition and multiplication. To perform binary bit operations, the VM uses a rather complicated scheme, where one table stores fixed byte-level operation results, and another table acts as a "scratch pad" to show how to decompose a 64-bit number into 8 bytes and then reassemble the result on multiple table rows.

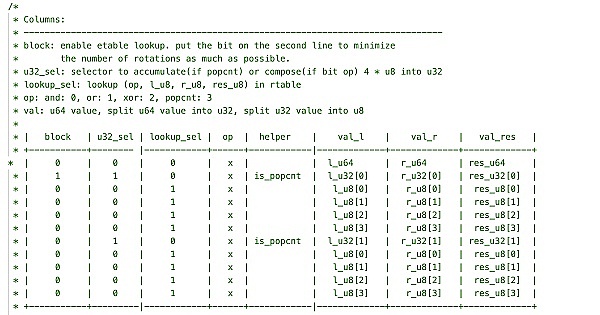
Snippet of the zkWasm bit table specification

In traditional programming languages, this is a very simple XOR operation, but here we need a lot of lemmas to verify the correctness of these auxiliary tables. For our instructions, we have:

Step 3: Execution Flow

Similar to traditional VMs, we need to make sure the value of the program counter is updated correctly. For sequential instructions like XOR, the program counter needs to be incremented after each step.

Since zkWasm is designed to run Wasm code, it is also necessary to ensure that the invariant properties of Wasm memory are always maintained throughout the execution process.

Traditional programming languages ​​have native support for data types such as Booleans, 8-bit integers, and 64-bit integers, but in ZK circuits, variables always vary in the range of integers modulo a large prime number (≈ 2254). Since VMs usually run with 64-bit numbers, circuit developers need to use a set of constraints to ensure that they have the correct numerical range, and formal verification engineers need to track invariants about these ranges throughout the verification process. Reasoning about the execution flow and execution table will involve all other auxiliary tables, so we need to check whether the range of all table data is correct.

Similar to the case of memory operation count management, zkVM requires a similar set of lemmas to verify control flow. Specifically, each call and return instruction requires the use of a call stack. The call stack is implemented using a table scheme similar to the data stack. For the XOR instruction, we do not need to modify the call stack; but when verifying the entire instruction, we still need to track and verify that the control flow operation count is correct.

Verifying this instruction

Let's put all the steps together and verify the end-to-end correctness theorem of the zkWasm XOR instruction. The following verification is done in an interactive proof environment, where each formal construction and logical reasoning step is subjected to the most rigorous machine checking.

As you can see above, it is possible to formally verify zkVM circuits. But it is a difficult task that requires understanding and tracking many complex invariants. This reflects the complexity of the software being verified: every lemma involved in verification needs to be handled correctly by the circuit developer. Given the high stakes, it is valuable to have them machine-checked by a formal verification system, rather than relying solely on careful human review.