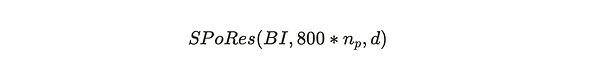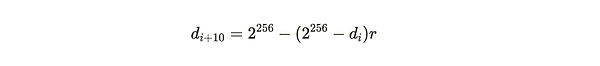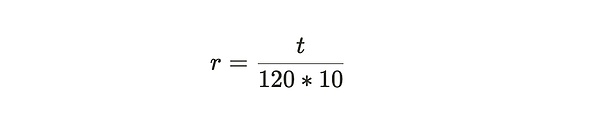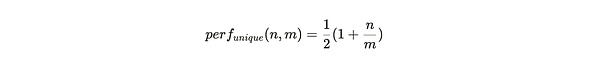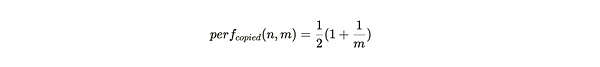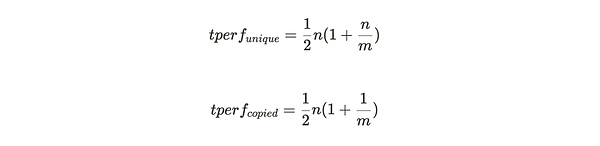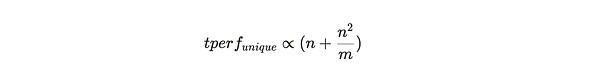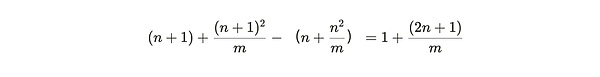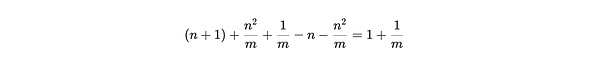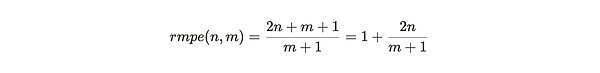Author: Gerry Wang @ Arweave Oasis, originally published on @ArweaveOasis Twitter
In Interpretation (III), we demonstrated the feasibility of #SPoRes through mathematical derivation. Bob and Alice in the article participated in this proof game together. In #Arweave mining, the protocol deploys a modified version of this SPoRes game. During mining, the protocol plays the role of Bob, and all miners in the network play the role of Alice together. Each valid proof of the SPoRes game is used to create the next block of Arweave. Specifically, the generation of Arweave blocks is related to the following parameters:
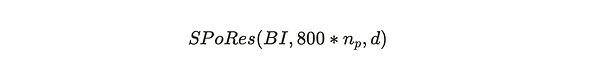
Where:
BI = Block Index of the Arweave network;
800*n_p = Each checkpoint unlocks a maximum of 800 hashes per partition, n_p is the number of partitions of 3.6 TB stored by the miner, and the multiplication of the two is the maximum number of hash operations that the miner can try per second.
d = The difficulty of the network.
A successful and valid proof is one that is greater than the difficulty value, and this difficulty value will be adjusted over time to ensure that an average of one block is mined every 120 seconds. If the time difference between block i and block (i+10) is t, then the adjustment from the old difficulty d_i to the new difficulty d_{i+10} is calculated as follows:
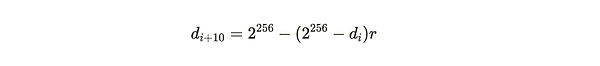
Where:
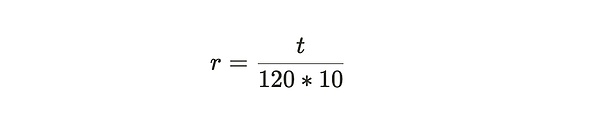
Formula Notes:From the above two formulas, it can be seen that the adjustment of network difficulty mainly depends on the parameter r, and r means the offset parameter of the actual time required for block generation relative to the standard time of 120 seconds per block expected by the system.
The newly calculated difficulty determines the probability of successful mining of a block based on each generated SPoA proof, as follows:

Formula Notes:After the above derivation, it can be obtained that the probability of successful mining under the new difficulty is the probability of success under the old difficulty multiplied by the parameter r.
Similarly, the difficulty of the VDF will be recalculated in order to keep the checkpoint cycle from occurring once per second in time.
Incentive mechanism for complete copies
Arweave generates each block through the SPoRes mechanism based on the following assumption:
Under incentives, both individual miners and group cooperative miners will use the maintenance of complete data copies as the best strategy for mining.
In the SPoRes game introduced earlier, the number of SPoA hashes released by two copies of the same part of the data set is the same as the full copy of the entire data set, which leaves the possibility of speculative behavior for miners. So Arweave made some modifications to this mechanism when it was actually deployed. The protocol divides the number of SPoA challenges unlocked per second into two parts:
One part specifies a partition in the partition stored by the miner to release a certain number of SPoA challenges;
The other part randomly specifies a partition in all Arweave data partitions to release SPoA challenges. If the miner does not store a copy of this partition, the number of challenges in this part will be lost.
You may feel a little confused here. What is the relationship between SPoA and SPoRes? The consensus mechanism is SPoRes, but why is the challenge released SPoA? In fact, there is a subordinate relationship between them. SPoRes is the general name for this consensus mechanism, which includes a series of SPoA proof challenges that miners need to do.
To understand this, we will examine how the VDF described in the previous section is used to unlock the SPoA challenge.

The above code details how to unlock the backtracking range consisting of a certain number of SPoA in the storage partition through VDF (encrypted clock).
Approximately every second, the VDF hash chain will output a checkpoint (Check);
This checkpoint Check will be used together with the mining address (addr), partition index (index(p)), and original VDF seed (seed) to calculate a hash value H0 using the RandomX algorithm. The hash value is a 256-bit number;
C1 is the backtracking offset, which is the remainder obtained by dividing H0 by the partition size size(p). It will be the starting offset of the first backtracking range;
The 400 256 KB data blocks within a continuous 100 MB range starting from this starting offset are the first backtracking range SPoA challenge that has been unlocked.
C2 is the starting offset of the second backtracking range, which is the remainder of H0 divided by the sum of all partition sizes, and it also unlocks 400 SPoA challenges for the second backtracking range.
The constraint of these challenges is that the SPoA challenges in the second range need to have SPoA challenges in the corresponding positions of the first range.
Performance of each packed partition
The performance of each packed partition refers to the number of SPoA challenges generated by each partition at each VDF checkpoint. When miners store Unique Replicas of a partition, the number of SPoA challenges will be greater than the number when miners store multiple backup Copies of the same data.
The concept of "unique copy" here is very different from the concept of "backup". For details, you can read the past article "Arweave 2.6 may be more in line with Satoshi Nakamoto's vision".
If the miner only stores the unique copy data of the partition, then each packaged partition will generate all the challenges of the first traceback range, and then generate the second traceback range that falls within the partition according to the number of stored partition copies. If there are m partitions in the entire Arweave weaving network, and the miner stores the only copy of n of them, then the performance of each packaged partition is:
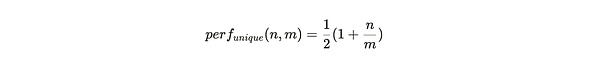
When the partitions stored by the miner are backups of the same data, each packaged partition will still generate all the challenges of the first traceback range. But only in 1/m cases will the second backtracking range be within this partition. This imposes a significant performance penalty on this storage strategy behavior, with the ratio of the number of SPoA challenges generated being only:
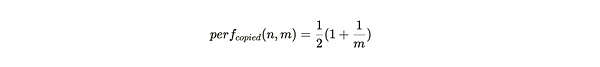
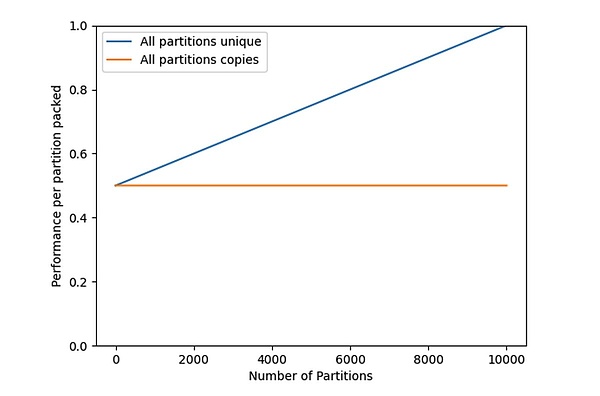
Figure 1: Performance of a given partition improves as a miner (or a group of cooperating miners) finishes packaging their datasets.
The blue line in Figure 1 is the performance of storing the unique copy of a partition, perf_{unique}(n,m), which intuitively shows that when miners store only a few copies of a partition, the mining efficiency of each partition is only 50%. When all data set parts are stored and maintained, that is, n=m, the mining efficiency is maximized to 1.
Total Hash Rate
The total hash rate (see Figure 2) is given by the following equation, which is obtained by multiplying the value of each partition by n:
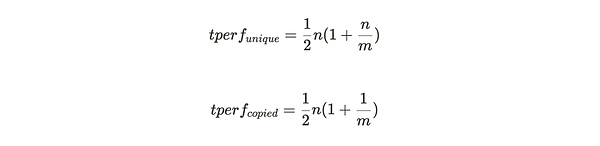
The above formula shows that as the size of the Weave network grows, if the unique copy of the data is not stored, the penalty function (Penalty Function) increases quadratically with the increase in the number of storage partitions.
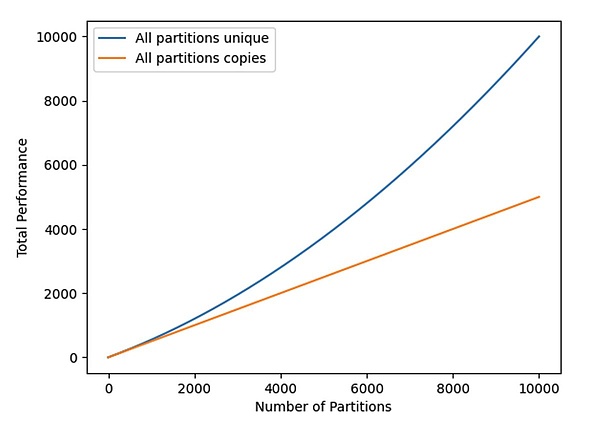
Figure 2: Total mining hash rate of unique and backup datasets
Marginal partition efficiency
Based on this framework, we explore the decision problem faced by miners when adding new partitions, that is, whether to choose to copy a partition they already have, or to obtain new data from other miners and package it into a unique copy. When they already store unique copies of n partitions from the maximum possible m partitions, their mining hashrate is proportional:
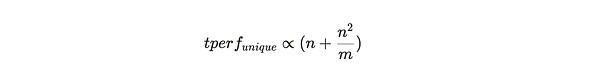
So the additional benefit of adding a unique copy of a new partition is:
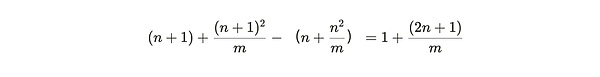
and the (smaller) benefit of copying an already packed partition is:
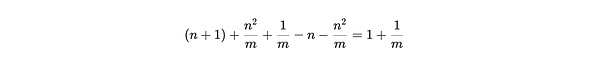
Dividing the first number by the second, we get the miner's relative marginal partition efficiency:
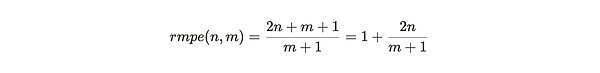
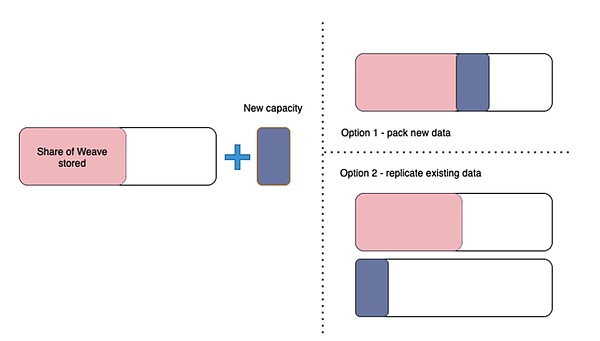
Figure 3: Miners are incentivized to build a complete replica (option 1) rather than making additional copies of the data they already have (option 2)
The rmpe value can be viewed as a penalty for miners to replicate existing partitions when adding new data. In this expression, we can treat m as approaching infinity and then consider the efficiency tradeoffs for different values of n:
The reward for completing a replica is highest when the miner has a nearly complete copy of the dataset. Because if n approaches m and m approaches infinity, the value of rmpe is 3. This means that, when close to a complete copy, finding new data is 3 times more efficient than repackaging existing data.
When miners store half of the Weave network, for example, when n= 1/2 m, rmpe is 2. This means that miners who find new data earn twice as much as those who copy existing data.
For lower values of n, the rmpe value tends to but is always greater than 1. This means that the benefits of storing a unique copy are always greater than the benefits of copying existing data.
As the network grows (m tends to infinity), miners' motivation to build a complete copy will increase. This promotes the creation of cooperative mining groups that jointly store a complete copy of at least one data set.
This article mainly introduces the details of the Arweave consensus protocol construction, of course, this is just the beginning of this core content. From the mechanism introduction and code, we can very intuitively understand the specific details of the protocol. I hope it can help everyone understand.
 Sanya
Sanya