作者:Vitalik Buterin,译者:Kurt Pan,XPTY
本文假设你熟悉 SNARK 和 STARK 工作原理的基础知识;如果你并不熟悉,建议阅读此文的前几节。特别感谢 Eli ben-Sasson、Shahar Papini、Avihu Levy 和 starkware 的其他人员提供的反馈和讨论。

https://en.wikipedia.org/wiki/Karatsuba_algorithm
https://polygon.technology/blog/plonky2-a-deep-dive
https://blog.icme.io/small-fields-for-zero-knowledge/
这一转变已经使得证明速度大幅提升,最显著的是 Starkware 能够在一台 M3 的笔记本电脑上 每秒证明 620,000 个 Poseidon2 哈希。具体来说这意味着,只要我们愿意信任 Poseidon2 作为哈希函数的部分,那么构建一个高效的 ZK-EVM 中最困难的部分之一就已经得到了高效解决。但这些技术是如何工作的,密码学证明(通常需要大整数来保证安全性)是如何在这些域上构建的?以及这些协议与更奇特的 构造(比如 Binius)又如何比较?这篇文章将探讨其中的一些微妙差别,会特别关注一种称为 Circle STARKs 的构造(在 Starkware 的 stwo、Polygon 的 plonky3 和 我自己的python 实现 中有实现),其具有一些独特的性质,旨在与高效的 Mersenne31 域兼容。
https://x.com/StarkWareLtd/status/1807776563188162562
https://vitalik.eth.limo/general/2022/08/04/zkevm.html
https://vitalik.eth.limo/general/2024/04/29/binius.html
https://www.irreducible.com/posts/binius-hardware-optimized-snark
https://eprint.iacr.org/2024/278
https://github.com/starkware-libs/stwo
https://github.com/Plonky3/Plonky3
https://github.com/ethereum/research/tree/master/circlestark
小域常见的问题
在进行基于哈希的证明(或实际上任何类型的证明)时,最重要的“技巧”之一是用证明有关多项式在随机点的求值以代替证明有关底层多项式的事情。

- https://en.wikipedia.org/wiki/Fiat%E2%80%93Shamir_heuristic

这个问题有两个自然的解决方案:

- https://www2.clarku.edu/faculty/djoyce/complex/mult.html

这里实现不是最优的(可以用Karatsuba优化),只是展示原理

常规 FRI


- https://eccc.weizmann.ac.il/report/2017/134/

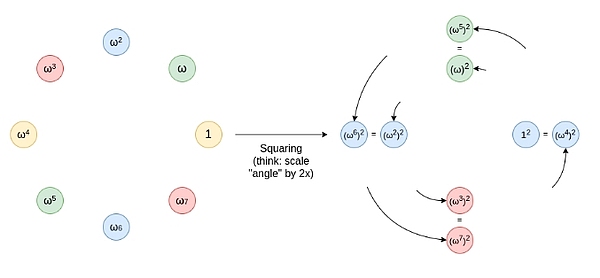

Circle FRI

- https://elibensasson.blog/why-im-excited-by-circle-stark-and-stwo/
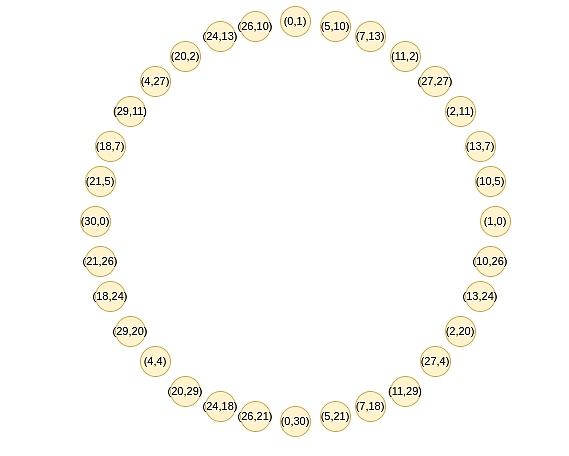
这些点遵循加法律,如果你最近学过 三角学 或 复数乘法,你可能会觉得这个定律很熟悉:
- https://unacademy.com/content/cbse-class-11/study-material/mathematics/algebra-of-complex-numbers-multiplication/

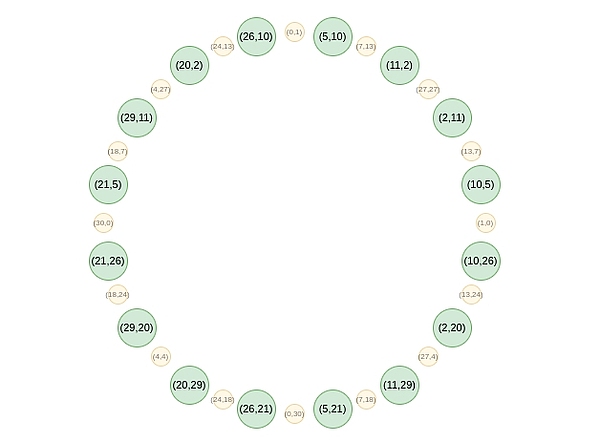

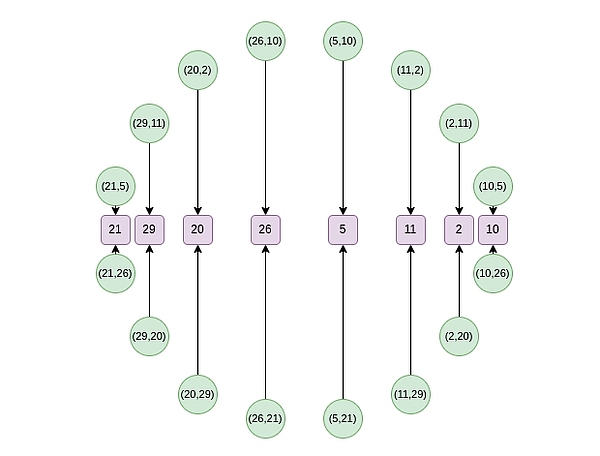
从第二轮往后,映射改变:

Circle FFTs

- https://vitalik.eth.limo/general/2019/05/12/fft.html


- https://www.researchgate.net/publication/353344649_Elliptic_Curve_Fast_Fourier_Transform_ECFFT_Part_I_Fast_Polynomial_Algorithms_over_all_Finite_Fields
从这里开始,让我们来了解一些更深奥的细节,对于实现circle STARK 的人来说,与常规 STARK 相比,这些细节会有所不同。
取商

- https://eprint.iacr.org/2019/336


消失多项式

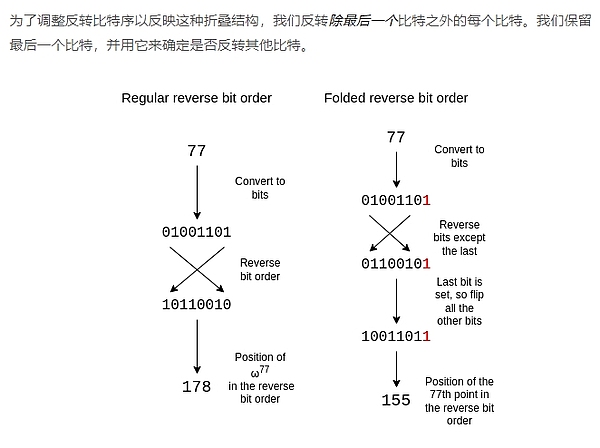
反转比特序


效率

因此,circle STARK 实际上非常接近最优了!Binius 甚至更强大,因为它允许混合搭配不同大小的域,从而为所有东西给出更高效的位打包。Binius 还提供了执行 32 比特加法的选项,且无需产生查找表的开销。然而,这些收益是以(在我看来)显著更高的理论复杂性为代价的,而circle STARK(以及基于 BabyBear 的常规 STARK)在概念上是相当简单的。
结论:我对 circle STARKs 怎么看?
与常规 STARK 相比,Circle STARK 并不会给开发者带来太多额外的复杂性。在实现的过程中,上述三个问题基本上就是我看到的与常规 FRI 相比的唯一区别。Circle FRI 所操作的“多项式”背后的数学原理是相当反直觉的,需要一段时间才能理解和领悟。但恰好这种复杂性被隐藏起来了使得开发者不会看到太多。Circle 数学的复杂性是封装过的,而不是系统性的。
理解circle FRI 和circle FFT 还是理解其他“奇异 FFT”的良好智力途径:最值得注意的是 二进制域 FFT,之前在 Binius 和 LibSTARK 中使用,还有更奇诡的构造,如 椭圆曲线 FFT,其使用几对一映射,可以很好地与椭圆曲线点运算配合使用。
https://github.com/ethereum/research/blob/master/binius/binary_ntt.py#L60
https://github.com/elibensasson/libSTARK
https://arxiv.org/abs/2107.08473
通过结合 Mersenne31、BabyBear 和 二进制域技术比如Binius,我们确实感觉得到正在接近 STARK “基础层”效率的极限。在这个时间点,我预计 STARK 优化的前沿将转向对哈希函数和签名等原语进行最高效的算术化(并为此目的优化这些原语本身)、进行递归构造以解锁更多并行化、对虚拟机进行算术化以提升开发者体验,以及其他上层任务。
 JinseFinance
JinseFinance
 JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance Catherine
Catherine Beincrypto
Beincrypto Coindesk
Coindesk Bitcoinist
Bitcoinist 链向资讯
链向资讯 Ftftx
Ftftx Cointelegraph
Cointelegraph