SAFE、新興企業の資金調達方法
SAFTとSAFEはシンプルで柔軟かつ効率的な資金調達方法であり、SAFTは通貨権への融資に、SAFEは株式への融資に利用され、わずか数ページで完了する。
 JinseFinance
JinseFinance
ソース: Denchainコミュニティ
現役プログラマーのためのZKPチュートリアル入門。
シマウマにはなぜ縞模様があるかご存知ですか?一説には、カモフラージュの一種だと言われています。シマウマが集まると、ライオンが獲物を見分けるのが難しくなります。ライオンは獲物を追い詰めるために、獲物を群れから隔離しなければならない[^1]。
人間も集団で隠れることを好む。その具体的な例が、複数の人間が集団の名の下に全体として行動する場合である。連邦議会論文はこの方法で作られた[^2]。 もう一つの例は、1930年代のフランスの数学者グループのペンネームであるブルバキである。これは、厳密さと公理的方法に焦点を当てた、現代数学の多くを完全に書き直すことにつながった[^3]。
デジタル時代において、グループチャットで物議を醸すようなメッセージを送りたいとしよう。どのグループであるかを明らかにすることなく、自分がそのグループであることを証明したいとします。そのために、デジタル領域ではどのように暗号を使えばいいのでしょうか?グループ署名と呼ばれるものを使えばいいのです。
伝統的に、グループ署名は数学的に非常に複雑で、実装が困難です。しかし、ゼロ知識証明(ZKP)を使えば、この数学的問題は簡単なプログラミング作業になります。この記事が終わるころには、あなた自身のグループ署名を書けるようになるでしょう。
この記事では、基本的なゼロ知識証明(ZKP)をゼロから書く方法を紹介します。
新しい技術スタックを学ぶときは、編集-構築-実行のサイクルをできるだけ早くスピードアップしたいものです。そうして初めて、自分の経験から学び始めることができるのです。
私たちはまず、環境をセットアップし、いわゆる信頼できるセットアップを実行する簡単なプログラムを書き、証明をできるだけ早く生成して検証することから始めます。その後、プログラムを改良する方法をいくつか見つけ、その改良を実装し、テストします。
特定のメッセージを送信したことを証明できる簡単な署名スキームを段階的に構築していきます。
# cloneリポジトリを作成し、準備スクリプトを実行します
git clone [email protected]:oskarth/zkintro-tutorial.git
cd zkintro-tutorial
#
less 。/scripts/prepare.sh
./scripts/prepare.sh
私たちは、./scripts/prepare.shをブラウズして、これが何をインストールするのか、あるいは手動でインストールするのかを確認することをお勧めします。実行すると、インストール完了とエラーが表示されるはずです。
問題が発生した場合は、最新の公式ドキュメント [7] を参照してください。
&&="template Multiplier2 () {
signal input a;
nbsp; signal input b;
signal input c;
; c <== a * b;
}
c;
これが私たちの特別なプログラム、_circuit_です。 [^6] 行ごとの解析:
テンプレートMultiplier() - テンプレートはほとんどのプログラミング言語でオブジェクトに相当し、抽象化の一般的な形式です
signal input a; - 最初の入力、a; 入力はデフォルトでプライベートです
signal input a; - 最初の入力、a; 入力はデフォルトでプライベートです。li>
signal input b; - 私たちの2番目の入力、b; 再びデフォルトではプライベート
signal output b; - 私たちの出力、c。code>;出力は常にpublic
c <== a * b; - これは2つのことを行います: cというシグナルをに割り当て、そしてcがaとbの積に等しくなるように制約します。bの積
component main = Multiplier2() - 私たちのメインコンポーネントをインスタンス化します
最も重要な行はc <== a * b;です。ここで実際に制約を宣言します。この式は、実際には、<--(代入)と===(方程式の制約)の2つの組み合わせです。 [^7] Circomの制約は、定数、加算、乗算を含む演算でのみ使用できる。これは、方程式の両辺が等しくなければならないことを強制します。 [^8]
制約はどのように機能するのか?数独のような文脈では、制約は「1から9の間の数」と言うかもしれません。しかし、サーコムの文脈では、これは単一の制約ではなく、より単純な方程式の制約(====)のセットを使って表現しなければならないものです。 [^9]
これはなぜでしょうか?それは基礎となる数学と関係があります。基本的に、ほとんどのZKPは多項式の計算を表す_算術回路_を使用します。多項式を扱う場合、定数を導入し、それらを加算し、乗算し、それらが等しいかどうかをチェックすることが簡単にできます。 [^10] 他の演算は、これらの基本演算で表現しなければならない。ZKPを書くためにこれを詳しく知っている必要はないが、フードの下で何が起こっているかを知っておくと役に立つかもしれない。 [
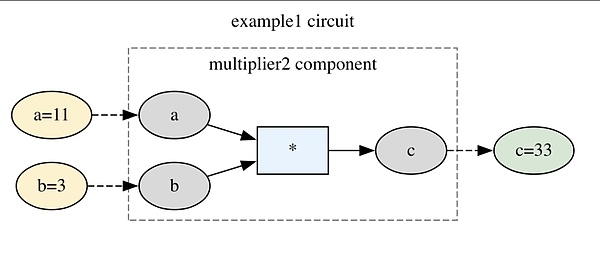
ZKPを書くためには、これらの基本的な操作で表現しなければなりません。
参考までに、最終的なファイルはexample1-solution.circomにあります。構文の詳細については、公式ドキュメント[9]を参照してください。example1.r1csとexample1.wasmファイルを作成するためにcircomを呼び出すための単純なラッパーです。
{
"pi_a": ["15932[...].3948", "66284[...]7222", "1"],
["17667[...]0525", "13094 [...]1600"],
["12020[...]"]。5738", 「10182[...]」。nbsp; "pi_c": ["18501(...)3969", "13175[...]です。3552", "1"],
"曲線": "bn128"
}
これは、いくつかの数学的オブジェクト(3つの楕円曲線要素)pi_a、pi_b、pi_cの形式で証明を指定します。code>の形で証明を指定する。[^20] また、プロトコル(groth16)と使用される_curve_(bn128、数学的実装の詳細は今は無視する)に関するメタデータも含まれる。これにより検証者は、この証明を正しく検証するためにどのように扱えばよいかを知ることができます。
この証明がいかに短いかに注目してください。私たちの特定のプログラムがいかに複雑であっても、この程度のサイズしかありません。これは、_Introduction to Friendly Zero Knowledge Proofs_[10]で説明したZKPの簡潔性の特性を示しています。
これは証人と回路に対応するすべての公開出力のリストです。この場合、cに対応する公開出力は1つです:33.[^21]
我々は何を証明したのでしょうか?私たちは2つの秘密の値、aとbを知っており、その積は33です。 これは前の記事で説明したprivacyの性質を示しています。
この証明は単独では役に立たないことに注意してください。
次に証明を検証してみましょう。実行:
just verify_proof example1
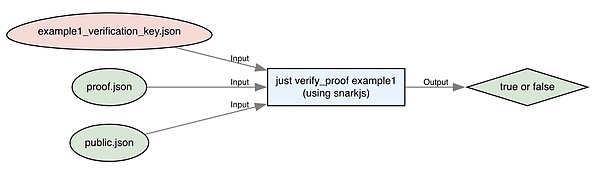
これには検証キー、公開出力、証明が必要です。これらによって、証明を検証することができる。Proof Validated "と表示されるはずである。検証者はプライベート入力には一切触れないことに注意。
出力を変更するとどうなるでしょうか?example1/target/public.jsonを開き、33を34に変更し、上記のコマンドをもう一度実行してください。
証明がもはや検証されていないことに気づくでしょう。
おめでとうございます。あなたは今、最初のZKPプログラムを書き、もっともらしい設定を行い、証明を生成し、最後にそれを検証しました!
ZKP の2つの重要な性質とその意味は何でしょうか?
証明者の役割と必要な入力は何ですか?検証者はどうでしょうか?
c <== a * b;という行が何をするのか説明してください。
なぜ信頼できる設定が必要なのでしょうか?その製品はどのように使うのでしょうか?
コード:example1を、証明を生成して検証するまでやり遂げましょう。
上記の回路で、私たちは2つの(秘密の)数の積を知っていることを証明しました。これは多くの暗号の基礎となっている素因数分解の問題と密接に関係しています。[^22] このアイデアは、非常に大きな数を持っている場合、その積が大きな数に等しくなるような2つの素数を見つけることは難しいというものである。逆に、2つの数の積が別の数に等しいかどうかを調べるのは非常に簡単である。[^23]
しかし、この回路には大きな問題がある。わかりますか?
入力を「1」と「33」に変えることは簡単にできる。つまり、数cは常に1とcの積になる。これではあまり印象的ではないだろう?
私たちがやりたいことは、aやbが1に等しくならないように、もう一つの制約を加えることです。
どのようにこの制約を追加し、どのような変更を加える必要があるのでしょうか?
これらの変更にはexample2フォルダを使います。残念ながら、a !== 1 と書くことはできません。[定数、足し算、掛け算、方程式のチェックで構成されていないからです。何かがない」ことをどのように表現するのか?
すぐに直感的に理解できるものではありませんし、この種の問題は回路を書く技術の見せ所です。このスキルを身につけるには時間がかかり、この最初のチュートリアルの範囲を超えています。幸いなことに、利用可能な多くの良いリソースがあります。[^25]
しかし、いくつかの一般的なイディオムがあります。基本的な考え方は、IsZero()テンプレートを使って式がゼロに等しいかどうかをチェックすることです。
可能性のある値を示すために真理値表[^26]を使うと便利なことが多い。以下はIsZero()の真理値表です:
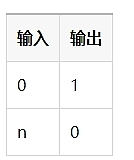
これは Circom のライブラリ circomlib に含まれているほど便利な構成要素です。circomlibには、他にも便利なコンポーネントがたくさんあります。[^27]
npm プロジェクト (JavaScript) を作成し、依存関係として追加することでインクルードできます。example2フォルダでは、このステップを行いました。関連するモジュールをインポートするには、example2.circomの一番上に次の行を追加します:
include "circomlib/circuits/comparators.circom";
example2.circomファイルを以下の行を含むように変更する:
just generate_proof example2
just verify_proof example2
期待通りに証明を生成し、検証しています。
example2/input.jsonへの入力を1と33に変更し、上記のコマンドを実行しようとすると、アサーションエラーが表示されます。つまり、入力が制約に違反しているため、Circomは証明を生成することさえできない。
すべてのプロセスを2回行ったので、一歩下がって、すべてのピースがどのように組み合わされているかを見てみましょう。
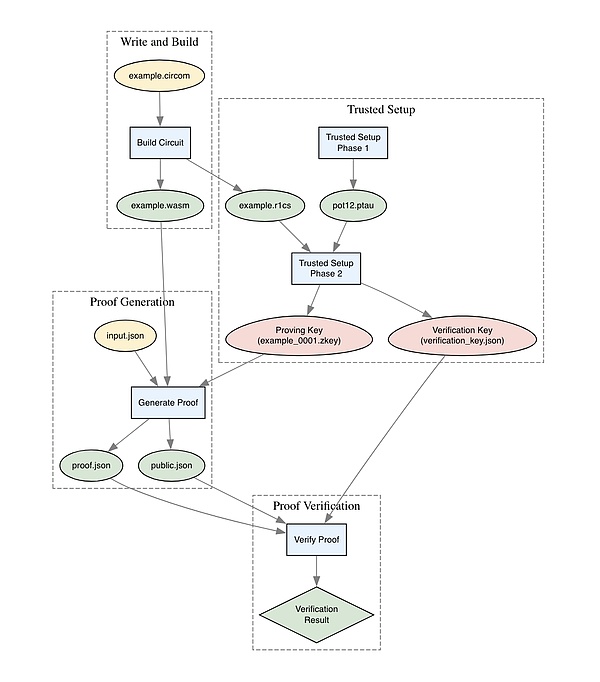
うまくいけば、物事は少し明確になり始めています。次は、回路をより使いやすくするために、少しパワーアップしてみましょう。
example2 のステージ1ではなく、ステージ2を実行しなければならないのはなぜでしょうか?
最後の例の主な問題は何だったのでしょうか?
コード:example2を証明を生成できなくなるまで完成させる。
上の回路で、2つの秘密の値の積がわかることを示しました。これだけではあまり役に立ちません。現実の世界で役に立つのは、_デジタル署名スキーム_である。これを使えば、自分が特定のメッセージを書いたことを他人に証明することができる。ZKPを使ってこれを実現するにはどうすればいいのだろうか?これを実現するためには、まずいくつかの基本的な概念をカバーしなければなりません。
ちょっと休憩して、お気に入りの飲み物を一杯飲みに行くにはいい時間だ。
デジタル署名はすでに存在し、デジタル時代にはどこにでもあるものです。現代のインターネットは、デジタル署名なしでは機能しません。通常、これらは公開鍵暗号を使って実装されます。公開鍵暗号方式では、秘密鍵と公開鍵があります。秘密鍵は自分だけが使うもので、公開鍵は公に共有され、自分の身元を表します。
電子署名スキームは以下の部分から構成されます:
Key Generation: 秘密鍵と対応する公開鍵を生成する
Signature: 秘密鍵を使って署名を作成する。
署名:秘密鍵とメッセージを使って署名を作成する
署名検証:メッセージが対応する公開鍵によって署名されていることを検証する
仕様が異なるように見えるかもしれませんが、私たちが書いたプログラムと上で説明した鍵生成アルゴリズムには1つの共通要素があります。より具体的には、トラップ関数です。トラップドアとは、落ちるのは簡単だが、(隠されたはしごを見つけない限り)登るのは難しいもののことである[^30]。
公開鍵暗号では、秘密鍵から公開鍵を構築するのは簡単ですが、その逆は非常に困難です。先ほどの手順も同じです。2つの秘密数が非常に大きな素数の場合、その積を元の値に変換するのは非常に難しい。現代の公開鍵暗号は通常、下部の_楕円曲線暗号_を使用します。
従来、このようなデジタル署名スキームのような暗号プロトコルを作成するには、多くの労力が必要で、巧妙な数学を含む特定のプロトコルを考え出す必要がありました。我々はそのようなことはしたくない。その代わりに、ZKPを使って同じ結果を達成するプログラムを書きたかったのです。
その代わりに:[^31]

私たちは、次のようなプログラムを書きたいだけです。プログラムを書きたいだけなのだ。
楕円曲線暗号を使う代わりに、よりシンプルな2つのツールを使います。
ハッシュ関数も一方向性関数です。例えば、コマンドラインでは、次のようにSHA-256ハッシュ関数を使うことができます:
commitment = hash(some_secret)
signaturesnbsp;signature = hash(some_secret, message)
この時点でいくつか疑問があるかもしれません。頭の中にある疑問を解決していきましょう。
まず、なぜこれが機能するのか、なぜZKPが必要なのかについてですが、誰かが証明を検証するとき、彼らは約束、メッセージ、署名にしかアクセスできません。秘密を明かすことなく、約束が秘密に対応していることを検証する直接的な方法はありません。この場合、証明を生成するときに秘密を「明かす」だけなので、秘密は安全なままです。
次に、なぜ公開鍵暗号ではなく、ZKPの内部でこれらのハッシュ関数と約束を使うのでしょうか?ZKP内で公開鍵暗号を使うことは絶対にできますし、そうする正当な理由があります。制約の面では、上記の選択肢よりも実装コストがはるかに高くなります。そのため、上記よりも遅く、複雑になります。次のセクションで見るように、ハッシュ関数の選択は非常に重要です。
最後に、すでに公開鍵暗号があるのに、なぜZKPを使うのでしょうか?この単純な例では、ZKPを使う必要はありません。しかし、この記事の冒頭で述べたグループ署名の例など、より興味深いアプリケーションのための構成要素として役立ちます。結局のところ、私たちは「プログラミング暗号」が欲しいのです。
たくさんありますね!幸いなことに、私たちはこの山を越えました。さっそくコーディングしましょう。最初はよくわからなくても心配しないでください。この推論方法に慣れるには時間がかかるだろう。
example3ディレクトリから作業を始めます。
デジタル署名を実装するためにまず必要なことは、鍵を生成することです。これは公開鍵暗号における秘密鍵と公開鍵に相当します。鍵はID(証明者であるあなた)に対応するので、それぞれidentity_secretとidentity_commitmentと呼ぶことにします。これらを合わせてIDペアを形成する。
これらは、署名するメッセージとともに回路の入力として使われる。公開出力として、署名、コミットメント、メッセージが得られる。これにより、誰かが署名が本当に正しいかどうかを検証することができます。
回路への入力としてIDペアが必要なので、これらを別に生成します:just generate_identity
This will produce something like:
include "circomlib/circuits/poseidon.circom";
Poseidon ハッシュテンプレートは次のように使用します:
component main {public [identity_commitment, message]} = SignMessage();
デフォルトでは、回路への入力はすべてプライベートです。このため、identity_commitmentとmessageを明示的にpublicとしてマークします。つまり、これらは公開出力の一部となる。
この情報によって、example3.circom回路を完成させるのに十分な知識が得られたはずです。それでもまだ行き詰まったら、完全なコードについてはexample3-solution.circomを参照してください。
前と同じように、回路を構築し、信頼できるセットアップのフェーズ2を実行する必要があります:
{
"identity_secret": "21879[...]7915",
"message": 42"
}
IDペアは自由に変更してください。をjust generate_identityを使って自分で生成したIDペアに自由に変更してください。結局のところ、あなたは自分のIDを自分自身に秘密にしておきたいのです!
メッセージが文字列として参照される単なる数字("42")であることに気づくかもしれません。残念ながら、制約が数学的に機能する方法(線形代数と_算術回路を使用)のため、私たちは数字しか使用できず、文字列は使用できません。回路が内部的にサポートする演算は、足し算や掛け算のような基本的な算術演算だけです。[
これはそれぞれ署名、約束、メッセージに対応します。 気をつけないとどうなるか見てみよう。 [^38] まず、 次に、出力にメッセージを含めない場合はどうなるでしょうか。私たちは証明を得ることができ、それは検証されます。しかし、メッセージは何でもあり得るので、実際に特定のメッセージを送ったことを証明することにはなりません。同様に、IDの約束を公開出力に含めない場合はどうなるでしょうか?つまり、IDの約束は何でもあり得るので、誰がメッセージに署名したのかは実際にはわかりません。 思考の練習として、これらの2つのキー制約のどちらかを省略した場合に何が起こるかを考えてみましょう。code> おめでとうございます![^39] デジタル署名スキームの3つの構成要素は何ですか? Poseidonのような「ZK-Friendlyハッシュ関数」を使う目的は何ですか? 約束とは何ですか?デジタル署名スキームでどのように使うことができますか? なぜIDの約束やメッセージを公開とするのでしょうか? なぜIDの約束と署名の制約が必要なのでしょうか? コード: 上記のデジタル署名スキームと、この記事で見てきたいくつかのトリックがあれば、記事の冒頭で述べたグループ署名スキームを実装するのに必要なツールはすべて揃っています。[^40] スケルトンコードは この回路によって、次のことができるようになります: Sign a message Certify that you are one of the three (Identity Commitment) ただし、どれかは明かさずに パズルのように考えることができます。重要な洞察は基本的に算術式に集約されます。できれば紙の上で解いてみてください。行き詰まったら、前と同じように解法をチェックする。 最後に、さらに挑戦したいのであれば、以下のような拡張があります: グループに何人でも入れるようにする 特定のメッセージに署名したことを証明する新しい回路 特定のメッセージに署名していないことを証明する新しい回路 古典的なツールを使ってこのような暗号プロトコルを作成するのは、多くの専門知識を必要とする大きな作業でしょう。[^42] ZKPを使えば、これらの問題をプログラミングのタスクとして扱うことで、午後には効率的で危険なことができるようになります。これは、私たちができることの氷山の一角にすぎません。 group signatureとregular signatureの違いは何ですか?どのように使い分けるのでしょうか? これらの質問はオプションであり、より多くの作業を必要とします。 コード:上記のグループ署名スキームを完成させる( コード: 上記のグループ署名の例を拡張します: より多くの人を許可し、 18歳であることを証明する「ZKアイデンティティ」システムをどのように設計しますか?証明したい他の属性は何ですか?また、どのような課題がありますか?既存のソリューションを研究し、その実装方法をよりよく理解する。 イーサのようなパブリックブロックチェーンでは、Layer 2 (L2)が、より速く、より安く、より多くのトランザクションを可能にするために使われることがあります。高いレベルで、ZKPを使用してL2をどのように設計しますか?どのように実装されているかをよりよく理解するために、既存のソリューションを研究してください。## 結論 このチュートリアル入門では、基本的なゼロ知識証明(ZKP)をゼロから書いて修正する方法に慣れました。プログラミング環境をセットアップし、基本的な回路を書きました。そして、もっともらしい設定を行い、証明を作成・検証した。いくつかの問題点を発見し、回路を改良した。その後、ハッシュ関数とプロミスを使った基本的なデジタル署名スキームを実装しました。 また、ゼロ知識証明なしでは実現が難しいグループ署名を実装するのに十分なスキルとツールも学びました。 ゼロ知識証明を書くために何が必要なのか、また編集-実行-デバッグのサイクルの実際について、よりよいメンタルモデルを理解していただけたと思います。これは、今後あなたが書くかもしれない他のゼロ知識証明プログラムにとって、どのような技術スタックを使うことになろうとも、良い基礎となるでしょう。 Hanno Cornelius氏、Marc Köhlbrugge氏、Michelle Lai氏、lenilsonjr氏、Chih-Cheng Liang氏に草稿を読んでいただき、フィードバックをいただきました。 Bourbaki Congress 1938 - Unknown, Public Domain, via Wikimedia[11] Kingsley Lockbox - P.S..Foresman, public domain, via Wikimedia[13] References [1] AI翻訳者: https://learnblockchain.cn/people/19584 [2] 翻訳チーム: [3] learnblockchain.co.jp/article...: https://learnblockchain.cn/article/9178 [4] A friendly introduction to zero knowledge: https://learnblockchain.cn/article/6184 [5] git リポジトリ: https://github.com/oskarth/zkintro-tutorial [6] git リポジトリ: https://github.com/oskarth/zkintro-tutorial [7]here: https://docs.circom.io/getting-started/installation/ [9]公式ドキュメント: https://docs.circom.io/circom-language/signals/ [10]Introduction to friendly zero-knowledge proofs: https://learnblockchain.cn/article/6184 [11]ウィキメディア: https://commons.wikimedia.org/wiki/File:Bourbaki_congress1938.png [12]Wikimedia: https://commons.wikimedia.org/wiki/File:Hartmann_zebras_hobatereS.jpg< [13]Wikimedia: https://commons.wikimedia.org/wiki/File.Kingsley_lockbox.jpg [14]AI Translator: https://learnblockchain.cn/people/19584 [15] こちら: https://github.com/lbc-team/Pioneer/blob/master/translations/9178.md [16]^2]: 参照[.Federalist Papers (Wikipedia): https://en.wikipedia.org/wiki/The_Federalist_Papers#Authorship [18]^8]: これは、想像されるかもしれませんが、制約を書くことをかなり難しくしています。Circomにおける制約の詳細については、[https://docs.circom.io/circom-language/constraint-generation/: https://docs.circom.io/circom-language/constraint-generation/ [19]^12]: 線形制約は、足し算だけで、線形結合として表現できることを意味します。線形の組み合わせで表現できることを意味します。これは定数を使った乗算と同じです。注意すべき主な点は、線形制約は非線形制約よりも単純であるということです。詳細は、[制約生成: https://docs.circom.io/circom-language/constraint-generation/ <を参照してください。"text-align: left;">[21]^13]: 数学的には、私たちがやっていることは、方程式 ["48968[...]5499", "48269 [...]7915", "42"]input.jsonでIDの約束をランダムなものに変更するとどうなるでしょうか。もはや証明を生成できないことに気づくでしょう。これは、まだ回路内部でIDの約束をチェックしているからです。IDの秘密と約束の関係を維持することは非常に重要です。signature<==signatureHasher.out演習
example3を、証明を生成して検証するまでやり遂げなさい。次のステップ
example4にあります。必要なコードは5~10行だけです。新しい構文はforループだけで、他のほとんどの言語と同じように動作します。[^41].revealを実装する。denyを実装する演習
質問
IsZero()がどのように実装されているか調べてください。example4を参照)。reveal および/または deny回路を実装します。謝辞
画像
Az * Bz = Cz<Z=(W,x,1)が成り立つことを確認しています。size: 14px;">である。A,B. and C は行列である。は行列であり、W は証人(プライベート入力)であり、xは公開入出力である。これを知っていると便利ですが、回路を書くときにこれを理解する必要はありません。詳しくは[Rank-1 Constraint System: https://docs.circom.io/background/background/#rank-1-constraint-system
[23]^17]: 私たちはこれを1-out-of-Nと呼んでいます。信頼モデルと呼ぶ。信頼のモデルは他にもたくさんあります。おそらく最もよく知られているのは多数決で、正しい決定を下す多数派を信頼するものです。これは基本的に民主主義や多数決がどのように機能するかということである。 [: #user-content-fnref-17
[24]^22]: _暗号的難易度の仮定_としても知られている。計算困難性の仮定 (Wikipedia): https://en.wikipedia.org/wiki/Computational_hardness_assumption#Common_cryptographic_hardness_assumptions
[25]^23]: 詳細は[https://en.wikipedia.org/wiki/]を参照。Integer_factorization: https://en.wikipedia.org/wiki/Integer_factorization
[25]^23]: [25]^23]を参照。="font-size: 14px;">[26]^24]: _asserts_を追加することもできますが、これらは実際には制約ではなく、入力をクリーンアップするためだけに使われます。https://docs.circom.io/circom-language/code-quality/code-assertion/:[https://docs.circom.io/circom-language/code-]を参照してください。quality/code-assertion/
[27]https://www.chainsecurity.com/blog/circom-assertions-misconceptions-and-deceptions: https://www.chainsecurity.com/blog/circom-assertions-misconceptions-and-
[28]^25]: 0xPARCによるこのリソースは、書き込みの技術について深く掘り下げたい場合に優れています(Circom)回路: [https://learn.0xparc.org/materials/circom/learning-group-1/circom-1/: https://learn.0xparc.org/materials/circom/learning-group-1/circom-1/
[29]^26]: 書き込み制約の性質上、このような状況はよく起こります。がしばしば発生します。https://en.wikipedia.org/wiki/Truth_table: https://en.wikipedia.org/wiki/Truth_table
[30]^27]: circomlibについての詳細は、[https://github.com/iden3/circomlib: https://github.com/iden3/circomlib
[31]^28]: 参照 [https://github.com/iden3/circomlib/blob/master/circuits/comparators.circom: https://github.com/iden3/circomlib/blob/master/circuits/comparators.circom<
[32]^29]: プロジェクト間でよく共有されます。size: 14px;">ptau セキュリティを強化するために、プロジェクト間でファイルを共有することがあります。詳しくは、[https://github.com/privacy-scaling-explorations/perpetualpowersoftau: https://github.com/privacy-scaling-explorations/perpetualpowersoftau
[33] https://github.com/iden3/snarkjs: https://github.com/iden3/snarkjs
[34]^30].: ここでの梯子は、逆に「難しい」方法で進むことを可能にする、ある種の価値を表している。別の言い方をすれば、南京錠のようなものです。鍵は簡単にかけられるが、鍵を持っていない限り開けるのは難しい。トラップドア関数は、より正式に定義されています。p> [35]^31]: Wikipediaからのスクリーンショット。参照[ECDSA (Wikipedia): https://en.wikipedia.org/wiki/Elliptic_Curve_Digital_Signature_Algorithm#Signature_verification_algorithm [36]^38]: 実際のデジタル署名スキームでは、複数のメッセージが交換される場合、暗号乱数を導入したい場合もあります。これはリプレイ攻撃を避けるためである。https://en.wikipedia.org/wiki/Replay_attack: https://en.wikipedia.org/wiki/Replay_attack [37]^40]: ZKPにおけるグループ署名の実装は、0xPARCに触発されたもので、[https://0xparc.org/blog/zk-group-sigs: https://0xparc.org/blog/zk-group-sigs [38]^41]: 参照[https://docs.circom.io/circom-language/control-flow/: https://docs.circom.io/circom-language/control-flow/ [39]^42]: 対照的に、[https://eprint.iacr.org/2015/043.pdf: https://eprint.iacr.org/2015/043.pdf
SAFTとSAFEはシンプルで柔軟かつ効率的な資金調達方法であり、SAFTは通貨権への融資に、SAFEは株式への融資に利用され、わずか数ページで完了する。
 JinseFinance
JinseFinanceソフトウェア主導でコミュニティが管理するトークン・ネットワークは、世界経済と社会全体に影響を与える巨大な可能性を秘めている。
 JinseFinance
JinseFinanceGolden Financeがお届けするGolden Web 3.0 Dailyは、ゲーム、DeFi、DAO、NFT、メタバース業界の最新・最速ニュースをお届けします。
 JinseFinance
JinseFinanceケイマン諸島対バハマ: FTX スキャンダルが両方の法域にどのように影響したか。
 Beincrypto
Beincrypto倒産した暗号ヘッジファンドは、かつて 1 億ドルの NFT コレクションを目指していましたが、現在は 100 万ドル未満の価値になっている可能性があります。
 Coindesk
Coindeskええ、それは本当です。 FBI は最近、DeFi を標的としたサイバー犯罪者のエクスプロイトについて警告を発しました。実際、DeFiプラットフォームは...
 Bitcoinist
Bitcoinistコインテレグラフとのインタビューで、MP Isola は、ジブラルタルの仮想通貨規制環境とビットコインへの関心について詳しく説明しました。
 Cointelegraph
Cointelegraphベルギーの議員は、同国で人気の仮想通貨取引プラットフォームであるBit4Youを通じて月給5,500ユーロをビットコインに交換する予定だ。
 Cointelegraph
Cointelegraphキルギスは仮想通貨交換とマイニングを規制しているが、同国には仮想通貨の流通を管理する法律がない。
 Cointelegraph
Cointelegraphキルギスタンは暗号交換と鉱業を規制していますが、国内での暗号通貨の流通を管理する法律はありません。
 Cointelegraph
Cointelegraph