현대 영지식 증명을 형성하는 10가지 필독 에세이

출처: 덴체인 커뮤니티

영지식 증명은 지난 40년 동안 극적으로 발전하여 전례 없는 수준의 정교함과 효율성에 도달했습니다. 오늘날에는 풍부한 아이디어와 혁신의 토대를 바탕으로 매일 새로운 논문과 프로젝트가 등장하고 있습니다.

이 모든 것이 어떻게 시작되었는지 궁금하신가요? 이 게시물에서는 영지식 증명의 역사를 살펴보고 이 분야를 형성하는 데 도움을 준 10개의 획기적인 논문을 살펴봅니다.

1 - 기원

골드바서, 미칼리, 랙오프 - 대화형 증명 시스템의 지식 복잡성 (1985) [^1]

우리의 첫 번째 이정표는 1985년의 중요한 논문으로 돌아갑니다! 이 논문은 오늘날에도 영지식 증명의 핵심이 되는 여러 용어와 기본 개념을 소개했습니다.

먼저, 이 논문은 두 개의 확률적 튜링 머신인 증명자와 검증자가 참여하는 양 당사자 프로토콜로 모델링된 증명 시스템을 정의합니다. 증명 시스템의 목표는 증명자가 주어진 입력 x가 형식 언어 L에 속한다는 것을 검증자에게 확신시키는 것입니다. 대부분의 초기 작업에서 증명자는 계산에 제한이 없는 반면 검증자는 다항식 시간 계산에 제한을 받습니다. 상호 작용이 끝나면 검증자는 "수락" 또는 "거부"를 출력합니다.

2 - 첫 번째 애플리케이션

파이아트, 샤미르 - 자신을 증명하는 방법: 신분 증명과 서명 문제에 대한 실용적인 해결책 (1986) [^2 )

영지식 증명에 대한 기초 연구가 발표된 지 1년 후에 발표된 피아트와 샤미르의 이 논문은 이러한 개념의 첫 번째 실용적 적용을 소개합니다. 이들은 두 가지 프로토콜, 즉 대화형인 식별 체계와 비대화형인 서명 체계를 제안합니다. 이 둘의 주요 차이점은 식별 체계에서는 제3자가 유효한 기록을 생성하여 허위 진술임을 스스로 확신할 수 있다는 것입니다. 반면 서명 프로토콜에서는 부정직한 증명자조차도 허위 진술을 확신할 수 없으므로 서명을 위조할 수 없습니다.

식별 체계는 검증자가 무작위 챌린지를 보내고 증명자가 그에 따라 응답하는 대화형 프로토콜로서 2차 잔여 증명 시스템을 적용합니다. 서명 체계는 검증자의 챌린지를 해시 함수에 대한 호출로 대체하여 이를 수정합니다.

작성자의 이름이 익숙하게 들리시나요? 이것은 현재 널리 알려진 강력한 일반 기법의 첫 번째 사례로, Fiat-Shamir 휴리스틱입니다. 이 기법은 검증자의 챌린지를 무작위 술어 기계(실제로는 암호화 해시 함수)에 대한 쿼리로 대체하여 모든 공개 코인 대화형 증명 시스템을 비대화형 시스템으로 전환할 수 있게 해줍니다.

3 - 실제로 무엇을 증명할 수 있을까요?

골드라이히, 미칼리, 위그더슨 - 영지식에서 모든 NP 문을 증명하는 방법과 암호화 프로토콜 설계 방법론(1987) [^3]

이 1986년 논문은 NP의 모든 언어가 영지식 증명 시스템을 인식한다는 놀라운 결과를 제시합니다. 이는 추가 정보를 공개하지 않고도 다항식 시간 내에 검증할 수 있는 모든 진술의 진리를 증명할 수 있다는 것을 의미하기 때문에 중요합니다. 저자들은 인접한 두 노드가 같은 색을 공유하지 않도록 그래프의 노드에 세 가지 색을 칠할 수 있는지 여부를 결정하는 문제인 그래프의 3색 가능성에 대한 증명 시스템을 제공함으로써 이를 입증합니다. 또한 이 증명은 확률적 암호화의 존재만을 가정합니다.

증명의 직관은 다음과 같습니다: 각 라운드에서

• 증명자는 세 가지 색상의 무작위 순열을 선택하고,
• 증명자는 각 노드에 대해 정렬 색을 지정하고,
• 증명자는 인접한 두 노드를 쿼리하여 해당 색을 요청합니다.
• 증명자는 쿼리된 노드의 색상을 공개하여 커미티를 엽니다.
• 색상이 일치하면, 증명자는 즉시 거부합니다.

이 프로토콜을 다항식으로 여러 번 실행하면 각 단계에서 개구부의 색이 무작위로 지정되므로 검증자는 아무런 정보 없이도 증명자가 유효한 3색을 알고 있다고 높은 확률로 확신할 수 있습니다!

이 작업에는 똑같이 주목할 만한 다른 두 개의 논문이 있습니다: All provable content can be proven in zero-knowledge [^4]는 IP의 모든 언어에 대해 영지식 증명 시스템이 있음을 보여주며, IP = PSPACE [^5]에서도 증명되었는데, 이는 IP가 PSPACE만큼 강력하다는 것을 보여줍니다.

4 - PCP와 간결한 비대화형 증명의 기원

Micali - 계산적으로 신뢰할 수 있는 증명. strong>컴퓨팅적으로 신뢰할 수 있는 증명 (2000) [^6]

Micali가 저술한 이 2000년 논문은 영지식 증명의 역사에 중요한 공헌을 한 논문입니다. SNARK라는 용어가 아직 만들어지지 않았음에도 불구하고 최초의 SNARK 구조로 간주할 수도 있습니다!

미칼리의 구조는 모든 확률 확인 가능 증명(PCP)을 간결하고 비대화형 증명으로 변환합니다. PCP는 적은 수의 비트만 읽어도 검증할 수 있는 증명이며, 핵심 결과인 PCP 정리 [^strong>]는 적은 수의 비트에 대한 증명입니다. /strong> [^7]은 NP의 모든 언어가 증명의 상수 비트만 읽으면 확인할 수 있는 PCP를 가지고 있음을 보여줍니다!

Micali의 구조는 다음과 같이 머클 트리를 사용합니다:

이 구조는 단순히 피아트-샤미르 휴리스틱을 적용하여 비대화형으로 만들 수 있습니다(이 변환의 대화형 버전은 킬리안[^8]이 제안했습니다). 이 논문은 또한 계산 효율성에 초점을 맞추고 있습니다. 실제로 검증자는 전체 증명을 받을 필요 없이 일정한 수의 비트와 인증 경로만 받으면 되기 때문에 증명을 간결하게 만들 수 있습니다. 이 시스템의 가장 큰 단점은 PCP 구조의 비실용성이며, 이로 인해 실용적인 논증을 생성하는 PCP의 일반화인 대화형 술어 기계 증명(IOP)이 개발되었습니다.

5 - 두 배로 효율적인 IP

Goldwasser, Kalai. 로스블룸 - 위임 계산: 머글을 위한 대화형 증명(2015) [^9]

이 논문은 효율성에 중점을 두고 있으며 널리 알려진 GKR 프로토콜을 소개하고, 사용 가능한 산술 회로를 위한 퍼블릭 코인 대화형 프로토콜을 소개합니다. 특히 검증자와 증명자 모두 다항식 시간 내에 실행되므로 대화형 증명에 있어 두 배의 효율성을 제공합니다.

이 프로토콜은 증명자와 검증자가 입력 팬 인이 2인 산술 회로에 동의하는 것으로 시작됩니다. 그런 다음 증명자는 입력값이 주어진 회로의 주장된 출력을 전송합니다. 프로토콜은 출력 레이어에서 시작하여 입력 레이어로 이동하면서 레이어별로 회로를 검사하는 방식으로 진행됩니다. 각 단계는 증명자가 입력 레이어에 도달하여 원래 입력과 일치하는지 확인할 수 있을 때까지 현재 레이어의 선언을 이전 레이어의 선언으로 축소합니다.

각 단계에서 사용되는 주요 프리미티브는 합계 확인 프로토콜 [^10]로, 이는 부울에 정의된 오라클 액세스 권한을 가진 v 변수 다항식 g의 값 합계에 대해 증명자가 검증자를 설득할 수 있도록 하는 대화형 증명입니다. hypercube:

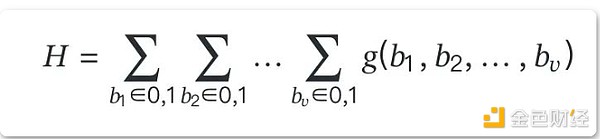
합산 검사 프로토콜과 GKR 프로토콜은 효율성과 단순성으로 인해 실무에서 널리 사용됩니다. 자세한 설명은 탈러의 노트[^11]에서 이러한 프로토콜에 대한 개요를 확인할 수 있습니다.

6 - 최초의 실용적인 SNARK

Gennaro, Gentry. 파르노, 레이코바 - PCP가 없는 이차 스팬 프로그램과 간결한 NIZK (2013) [^12]

이제 기사로 이동합니다. 논문으로 이동합니다! 이 연구는 비효율적인 PCP 정리에 의존하지 않는 SNARK를 만드는 것을 목표로 하는 SNARK 연구의 정점을 찍었습니다. PCP 정리는 이론적인 SNARK 구조를 제공하지만 실제 적용하기에는 너무 느리기 때문에 연구자들은 보다 효율적인 대안을 찾기 위해 노력해왔습니다. 예를 들어, Groth는 2010년에 이선형 그룹과 쌍을 기반으로 하는 비대화형 논증 시스템을 제안했지만[^13], 증명자에게 2차적인 시간이 필요했습니다. 그러나 이 논문은 선형 증명 시간을 구현하여 실제 적용을 위한 상당한 개선을 보여줍니다.

이 작업은 피노키오 프로토콜[^14], 궁극적으로 유명한 Groth16[^15] 증명 시스템과 같은 다른 중요한 프로토콜의 길을 열었습니다. . 이 논문은 또한 이러한 시스템에서 여전히 중요한 구성 요소인 이차적 스패닝 절차와 이차적 산술 절차에 대해서도 설명합니다.

이러한 구조의 중요한 단점은 공개 참조 문자열의 생성 단계에서 생성된 비밀 정보(흔히 독성 폐기물이라고도 함)가 올바르게 파기되지 않으면 다음과 같은 용도로 사용될 수 있다는 것입니다. 잘못된 증명을 생성할 수 있습니다. 또한 이 설정은 일반적인 설정이 아니기 때문에 각 회로마다 새로운 설정이 필요합니다. 이러한 한계에도 불구하고 생성된 증명의 크기는 다른 구조 중 가장 작기 때문에 다양한 애플리케이션에 널리 사용됩니다.

초기 영향력 있는 블록체인 애플리케이션인 Zerocash[^16]의 첫 번째 반복이 이러한 시스템을 기반으로 구축되었다는 점도 주목할 만합니다.

7 - PlonK SNARK

Gabizon, Williamson , 시오보타루 - PlonK: 에큐메니칼 지식의 비대화형 논증에 대한 라그랑주 기저에 대한 순열 (2019) [^17]

이 2019 Impact 논문은 검증자가 여러 다항식에 오라클 액세스하고 이를 평가할 수 있는 대화형 다항식 오라클 증명(IOP)에 기반한 시스템인 PlonK SNARK에 대해 설명합니다. 선택한 지점에서 평가할 수 있습니다. 이 시스템은 다양한 다항식 가젯을 사용해 다항식에 대한 진술을 증명하는데, 그 중 가장 주목할 만한 것은 증명자가 도메인에 대한 평가의 곱이 1임을 증명할 수 있는 Great Product 인수입니다. 이를 사용해 두 수열이 서로의 치환임을 증명하는 Placement 인수를 구성할 수 있습니다. 이러한 가젯을 사용하여 증명자는 모든 산술 회로에 대한 증명을 구성할 수 있고, 검증자는 비대화형 방식으로 이를 검증할 수 있습니다.

실제로 오라클 접근은 다항식 커밋 체계(PCS)를 통해 구현되며, 이를 통해 증명자는 다음을 수행할 수 있습니다.

• < 섹션 스타일="text-align: 왼쪽;">다항식에 커밋하고
• 특정 지점에서 해당 다항식을 평가합니다
• 제공합니다. strong>해당 다항식의 열린 값을 제공합니다.

이를 통해 검증자는 임의의 지점에서 다항식을 쿼리하고 IOP 관계를 검증할 수 있습니다. 논문에서 제안한 PCS는 효율적이고 실용적인 KZG 커밋 방식[^18]으로, 증명자는 다항식을 단일 그룹 요소로 커밋하고 검증자는 여러 타원 곡선 쌍을 계산하여 열린 값을 확인할 수 있으며, KZG를 통해 증명자는 다항식을 하나의 그룹 요소로 커밋할 수 있습니다. KZG는 그럴듯한 설정이 필요하지만, 일반적이며 설정 후 모든 회로에서 사용할 수 있습니다. 그러나 PlonK는 다른 PCS 체계와 결합하여 투명한 인수 체계에 맞게 조정할 수 있습니다.

또한, PlonK의 대체 인자는 인자 찾기에 영감을 주었습니다. 조회 인수를 사용하면 증명자가 수열의 모든 요소가 다른 수열에 포함되어 있음을 보여줄 수 있으며, 이는 zkVM 아키텍처에 유용합니다. 조회 인자를 사용하면 증인을 더 작은 추적들로 분해하고 이들 간의 조회 관계를 증명할 수 있으므로 복잡한 증명을 더 효율적으로 수행할 수 있습니다.

8 - STARKs

Ben-Sasson, Bentov. Horesh, Riabzev - 확장 가능하고 투명하며 양자 이후에도 안전한 계산 무결성 (2018) [^19]

이 논문에서는 리드-솔로몬 코드의 근접성 테스트를 위한 IOP 프로토콜인 FRI [^20]에 기반한 또 다른 인기 증명 시스템인 STARK 증명 시스템에 대해 설명합니다. STARK에서 증명자는 도메인에 머클 트리를 구축하여 다항식 평가를 커밋합니다. 커밋된 값은 처음에 알 수 없으므로 증명자는 FRI를 사용하여 이러한 평가가 충분히 낮은 차수의 유효한 다항식을 형성하는지 확인합니다. 이 프로토콜은 다항식 커밋 체계로도 사용할 수 있으며, 검증자는 언제든지 커밋 다항식의 평가를 확인할 수 있습니다.

스타크의 가장 매력적인 특징 중 하나는 이산 로그 문제와 같은 다른 암호화 가정이 아닌 암호화 충돌 방지 해시 함수에만 의존한다는 점입니다. 충돌 방지 해시 함수는 양자 공격에도 안전한 것으로 널리 알려져 있기 때문에, 양자 이후의 잠재적 보안 측면에서 STARK가 유리합니다. 또한, STARK는 <강력>투명하므로 신뢰할 수 있는 설정이 필요하지 않습니다. 또한, 특정 회로에 국한되지 않는 범용성이 있어 다양한 애플리케이션에서 유연하게 사용할 수 있습니다.

9 - 재귀

Valiant - 점진적으로 검증 가능한 계산 또는 지식 증명은 시간/공간 효율성을 의미합니다. (2008) [^21]

수년에 걸쳐 등장한 중요한 개념 중 하나는 재귀로, 간단히 말해 하나의 증명을 사용하여 다른 증명의 정확성을 증명할 수 있다는 것을 의미합니다. 이 논문에서 제시된 시나리오는 잠재적으로 긴 계산 결과의 정확성을 증명하고자 하는 증명자를 포함합니다. 튜링 머신이 주어지면 상태 전달 함수의 개별 단계의 정확성을 증명할 수 있지만 이것만으로는 충분하지 않으며, 일련의 상태 전달로 구성된 전체 계산의 정확성을 증명하고자 합니다.

증분 검증 가능 컴퓨팅(IVC)의 개념은 다음과 같습니다: S1에서 S2로의 단일 상태 전송이 정확하다는 것을 증명할 수 있다고 가정해 보겠습니다. 그러면 두 가지 증명을 하나로 결합할 수 있습니다. 증명자는 두 가지 유효한 증명을 알고 있음을 보여줍니다.

병합된 증명은 S1에서 S3으로의 전송이 옳다는 것을 증명자에게 확신시킵니다. 이 과정은 몇 단계까지 반복할 수 있으며, 임의로 긴 계산을 하나의 증명으로 압축할 수 있습니다(더 구체적으로는 다항식으로 긴 계산).

이 구조는 두 가지 주요 가정에 의존한다는 점에 유의하는 것이 중요합니다.

• 증명 체계의 건전성: 증명자는 개별 상태 전이에 대한 증명의 존재를 증명할 뿐만 아니라 이러한 증명을 알고 있다는 사실도 증명해야 합니다. 직관적으로, 귀납적 지식 추출성을 통해 개별 상태 전이에 대한 모든 증명을 추출할 수 있습니다.
• 실제 해시 함수는 무작위 예측자: 이것은 더 강력한 가정입니다. 그러나 합산 증명에서 중립적 증명의 정확성을 검증할 필요가 있습니다.

이 구조는 이론적으로는 강력하지만 실제로 적용하기에는 비용이 많이 듭니다. 이 문제를 해결하기 위해 효율성을 개선하기 위한 새로운 접근 방식이 제안되었습니다. 그중 하나가 폴딩 방식[^22]을 사용하는 것인데, 이는 가정을 완화하고 재귀적인 SNARK 유효성 검사의 필요성을 피할 수 있습니다. 폴딩의 개념은 두 개의 증명인 π와 π′가 주어지면 이를 하나의 증명인 π″로 "폴딩"할 수 있다는 것입니다. 검증자는 접힌 인스턴스가 만족스럽다면 원래 인스턴스도 만족스럽다고 믿습니다.

10 - zkVM을 통한 검증 가능한 계산

Ben-Sasson, Chiesa, Tromer, Ben-Sasson 및 기타. Chiesa, Tromer, Virza - 폰 노이만 아키텍처를 위한 깨끗하고 비대화형 제로 지식(2014) [^23]

이 마지막 논문에서는 최초의 실용적인 영지식 가상 머신< /strong>(zkVM)에 대해 설명합니다. /임의의 프로그램을 실행하고 이러한 계산의 정확성에 대한 증명을 생성할 수 있는 가상 머신인 (zkVM) 구성에 대해 설명합니다. 설명한 머신은 폰 노이만 아키텍처를 따르며, 이는 프로그램과 데이터가 동일한 메모리에 저장된다는 것을 의미합니다. 대부분의 최신 CPU는 이 패러다임에 기반하고 있으므로 이론적으로 기존 컴퓨터에서 실행할 수 있는 모든 프로그램이 이 아키텍처에서도 실행될 수 있습니다.

이 논문은 vnTinyRAM이라는 RISC 아키텍처를 설명하고 이 명령어 집합에 포팅된 C 컴파일러를 보여줍니다. 이 증명 시스템은 프로그램 실행의 정확성을 정해진 단계까지 검증하도록 설계되었습니다. 기본 아이디어는 회로를 명령어 수 제한에 도달할 때까지 전개되는 반복 상태 전이 함수로 구성하는 것입니다.

오늘날 zkVM은 점점 더 인기를 얻고 있습니다. 주요 장점 중 하나는 사용자가 고급 프로그래밍 언어로 프로그램을 작성하고 이를 사용하여 증명을 생성할 수 있다는 것입니다. 많은 표준 알고리즘과 데이터 구조가 이미 이러한 고수준 언어에 정의되어 있기 때문에 수동으로 회로를 작성하는 것보다 상당한 이점을 제공합니다. 또한 개발자는 익숙한 계산 모델을 재사용할 수 있으므로 영지식 증명을 사용하는 데 필요한 학습 곡선을 크게 줄일 수 있습니다.

많은 zk-rollup이 이 모델을 기반으로 한다는 점도 주목할 가치가 있습니다. 예를 들어, 이더넷 가상 머신(EVM) 실행을 지원하는 zk-롤업은 zkVM을 사용하여 EVM 실행의 정확성을 증명합니다.

마지막으로, 이 논문은 영지식 증명 시스템에 사용하기에 최적화된 자체 아키텍처에 대해 설명합니다. zk 친화적인 아키텍처의 또 다른 유명한 예로는 STARK를 사용한 증명에 최적화된 튜링 완전 CPU인 Cairo CPU 아키텍처[^24]가 있습니다.

참고 논문

[^1]: Goldwasser, S., Micali, S., & Rackoff, C. ( 1985). 대화형 증명 시스템의 지식 복잡성. (링크) ︎

[^2]. 피아트, A., & 샤미르, A. (1986). 자신을 증명하는 방법: 식별 및 서명 문제에 대한 실용적인 솔루션. (링크) ︎
[^3]: Goldreich, O., Micali, S., & Wigderson, A. .(1987). 영지식에서 모든 NP 문을 증명하는 방법과 암호화 프로토콜 설계 방법론. (링크) ︎
[^4]:  Ben-Or, M., Goldreich, O. ., Goldwasser, S., Håstad, J., Kilian, J., Micali, S., & Rogaway, P. (1990). 증명 가능한 모든 것은 영지식에서 증명 가능하다. (링크) ︎
[^5]:  Shamir, A. (1992). (링크) ︎
[^6]: Micali, S. (2000). 계산적으로 건전한 증거. ([링크] (https://people.csail.mit.edu/silvio/Selected 과학 논문 / 증명 시스템 / 계산적으로 건전한 _Proofs.pdf)) ︎
[^7]:  Cook, S. A. (1971). 증명 검증과 근사 문제의 난이도. (링크) ︎
[^8]:  Kilian, J. (1992, July). 효율적인 영지식 증명과 논증에 대한 참고 사항. (링크) ︎
[^9]: Goldwasser, S., Kalai, Y. T., & Rothblum, G. N. (2015). 계산 위임: 머글을 위한 대화형 증명 (링크, 저스틴 탈러의 이 노트도 참조) ︎
[^10]: Lund, C., Fortnow, L., Karloff, H., &. 앰프; 니산, N. (1992). 대화형 증명 시스템을 위한 대수적 방법.(링크) ︎
[^11]:  Thaler, J. (2015). GKR 프로토콜에 대한 참고 사항. (링크) ︎
[^12]: Gennaro, R., Gentry, C., Parno, B., & Raykova, M. (2013). PCP가 없는 이차 스팬 프로그램과 간결한 NIZK.(링크) ︎
[^13]: Groth, J. (2010). 짧은 페어링 기반 비대화형 영지식 인자. (링크) ︎
[^14]: Parno, B., Howell, J., Gentry, C., & Raykova, M. (2016). 피노키오: 거의 실용적인 검증 가능한 계산.(링크) ︎
[^15]:  Groth, J. (2016). 페어링 기반 비대화형 인수의 크기에 대해.(링크) ︎
[^16]:   Sasson, E. B., Chiesa, A., Garman, C., Green, M., Miers, I., Tromer, E., & Virza, M. (2014). 제로캐시: 비트코인을 통한 탈중앙화 익명 결제.(링크) ︎
[^17]:  Gabizon, A., Williamson, Z. J., & Ciobotaru, O. (2019). 플롱크: 지식의 에큐메니칼 비대화형 논증에 대한 라그랑주 기반에 대한 순열.(링크) ︎
[^18]: Kate, A., Zaverucha, G. M., &. 골드버그, I. (2010). 다항식과 그 응용에 대한 일정한 크기의 약속.(링크) ︎
[^19]:  Ben-Sasson, E., Bentov, I., Horesh, Y., & Riabzev, M. .(2018). 확장 가능하고 투명하며 양자 이후 안전한 계산 무결성.(링크) ︎
[^20]:  Ben-Sasson, E., Bentov, I., Horesh, Y., &. Riabzev, M. (2018). 빠른 리드-솔로몬 대화형 오라클 근접성 증명.(링크) ︎
[^21]: Valiant, P. (2008). 점진적으로 검증 가능한 계산 또는 지식 증명은 시간/공간 효율성을 의미합니다. (링크) ︎
[^22]: Kothapalli, A., Setty, S., &. 치알라, I. (2022, 8월). Nova: 폴딩 스키마에서 재귀적 영지식 인수.(링크) ︎
[^23]: Ben-Sasson, E., Chiesa, A., Tromer, E., & Virza, M. (2014). 폰 노이만 아키텍처를 위한 간결한 비대화형 제로 지식.(링크) ︎
[^24]: Goldberg, L., Papini, S., & Riabzev, M. (2021). 카이로-튜링이 완성한 STARK 친화적인 CPU 아키텍처. (링크) ︎