게르하르트 코드의 양자 위기? G-코드를 둘러싼 학계의 논쟁에 관한 기사

블록체인에 대한 양자 보안 위협과 대응

2024년 3월 10일, 이더리움의 공동 창립자인 비탈릭 부테린은 "양자 비상사태에서 대부분의 사용자 자금을 구하기 위한 하드포크 방법"[1]이라는 새로운 기사를 이더리움 연구 포럼(ethresear.ch)에 게시했습니다. 포럼(ethresear.ch)에서 "양자 비상 상황에서 대부분의 사용자 자금을 보호하는 하드포크 방법"[1]이라는 최신 기사를 통해 이더리움 생태계에 대한 양자 컴퓨팅 공격의 위협을 탄력적인 포크 전략과 안티퀀텀 암호화를 통해 사용자의 자금은 안전합니다.

블록체인에 대한 양자 보안 위협은 정확히 무엇인가요?

양자 컴퓨팅은 양자역학을 이용해 양자 정보 단위를 조절하여 새로운 컴퓨팅 모델을 계산하는 것으로, 1980년대에 제안된 개념으로 양자 컴퓨터 도입 후 10년 동안은 추상적인 이론 단계에 머물렀습니다. 1990년대 중반까지 두 가지 양자 알고리즘인 쇼 알고리즘[3](많은 수의 분해와 이산 로그 어려움을 해결하기 위한 다항식 시간)과 그로버 알고리즘[4](철저한 검색 문제의 비정형 데이터가 가속의 제곱을 제공하기 위해)이 제안되어 양자 컴퓨팅이 추상 이론 단계에서 벗어나 새로운 단계의 물리적 캐리어 연구 및 개발로 전환되었으며 현재 양자 계산으로 불립니다. 새로운 단계는 이제 양자 컴퓨터로 알려져 있습니다. 다음 차트는 1998년부터 2026년까지 양자 컴퓨터의 물리적 양자 비트 개발 로드맵을 보여줍니다:

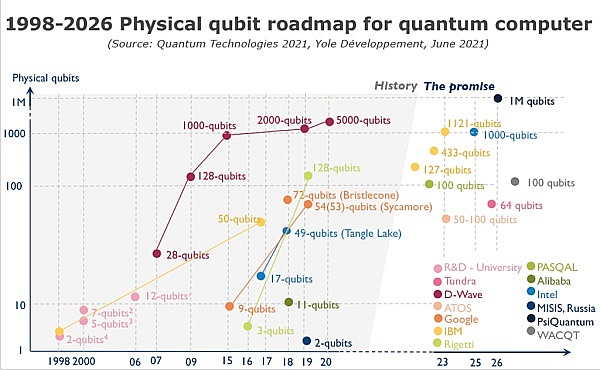
양자 컴퓨팅은 만병통치약이 아니며 모든 컴퓨팅 문제에 대한 해답이 아닙니다. 현재 양자 컴퓨팅은 자연에서 일어나는 과정을 시뮬레이션(화학 및 생물 공학), 해독(대부분의 기존 암호화 시스템 해독, 사이버 보안), 최적화(실현 가능한 옵션 중에서 최적의 솔루션 찾기, 금융, 공급망) 및 기타 도메인별 문제에서 계산적 우위를 발휘하는 데 사용될 수 있습니다.

블록체인이 현재 널리 사용되는 이유는 기본 암호화가 제공하는 보안을 기반으로 서로 다른 청구인 간의 협업에 새로운 신뢰 기반을 제공하기 때문입니다.

• 신원 확인 및 거래 확인: 비대칭 공개-개인 키 쌍을 기반으로 사용자가 신뢰할 수 있는 신원을 설정하고 통합된 방식으로 신원 정보를 관리합니다. 디지털 자산 인증을 위한 디지털 서명을 통해 개인 키 소유자의 유효 서명이 실제로 자산의 소유권을 갖습니다.

• 핵심 합의 및 운영 보안: 해시 함수, 임계값 서명, 검증 가능한 랜덤 함수 등과 같은 최신 암호화 기술을 기반으로 합의 메커니즘을 구축하여 합의 메커니즘의 안전성을 보장합니다.

• 개인정보 보호 및 안전한 공유: 영지식 증명, 안전한 다자간 계산, 완전 동형성 및 기타 다양한 기능의 암호화 기술을 기반으로 개인 정보 보호 체계를 구축하여 블록체인에서 데이터를 안전하게 공유할 수 있도록 합니다.

• 제어 가능한 규제 및 규정 준수 애플리케이션: 링 서명, 동형 암호화 체계, 암호화 주소 및 비밀 공유와 같은 암호화 기술을 통합 및 배포하여 블록체인 거래의 안전한 규제를 보장합니다.

공개 키 암호화의 사용은 크게 온체인 거래에서 조작을 방지하는 데 사용되는 디지털 서명 메커니즘과 노드 간 통신에 사용되는 보안 전송 프로토콜로 나눌 수 있습니다. 쇼 알고리즘의 영향으로 인해 위 공개 키 암호의 보안을 효과적으로 보장할 수 없습니다. 암호 해독에 특화된 양자 컴퓨터를 대규모로 적용하는 데 필요한 시간을 고려하는 동시에 블록체인에 저장된 데이터를 보존해야 하는 기간과 기존 블록체인 시스템을 양자 수준의 보안으로 업그레이드하는 데 걸리는 시간도 고려해야 합니다. 후자의 두 가지를 합산한 시간이 전자의 시간보다 크다면, 블록체인 상의 데이터는 양자 컴퓨팅으로 인한 심각한 보안 위협에 노출된 것입니다.

퀀텀 컴퓨팅의 급속한 발전으로 인해 연산 능력이 증가하는 현재 상황을 고려할 때, 현재 보안 위험에 효과적으로 대처할 수 있는 두 가지 주요 기술 경로가 있습니다.

1. 물리적 장비의 도움 없이 새로운 수학적 퍼즐을 기반으로 하는 양자 암호 기술 경로

2. 특수한 물리적 장비의 도움을 받는 물리적 원리 기반 양자 암호 기술 경로

3. 물리적 원리 기반 양자 암호 기술 경로

4. 특수한 물리적 장비의 도움을 받는 양자 암호 기술 경로

   [5]>; 기술 경로.

양자 암호 마이그레이션은 기존 암호화 보안 전제와의 호환성 측면에서 장기적인 보안 보장 하에 블록체인이 양자 수준의 보안으로 업그레이드될 수 있도록 양자암호 마이그레이션을 미리 배포하여 랜딩 구현 검증 등 다양한 요소를 고려하여 고려할 수 있습니다. 기존 블록체인에서 사용되는 공개키 암호 알고리즘을 양자 보안 수준의 포스트 양자 암호 알고리즘으로 업그레이드하는 것은 다음과 같은 특성을 최대한 만족하는 것이 이상적입니다.

• 작은 키와 짧은 서명: 블록체인 상의 모든 거래는 에는 서명 정보가 포함되며, 거래를 확인하기 위한 공개 키도 체인에 저장됩니다. 키와 서명이 너무 크면 블록체인의 저장 비용과 통신 오버헤드가 크게 증가합니다.

• 계산 효율성: 블록체인 운영 중 각 시간대에 처리할 수 있는 거래의 수는 알고리즘, 특히 서명 검증 알고리즘의 실행 시간과 크게 관련이 있습니다. 알고리즘의 연산 효율성이 높을수록 고성능 블록체인 애플리케이션을 더 잘 지원할 수 있습니다.

양자 암호 개발 현황

양자 암호는 한마디로 양자 컴퓨터에 의한 기존 암호화 알고리즘에 대한 공격에 저항할 수 있는 1세대 암호화 알고리즘입니다. 1세대 암호화 알고리즘 :

• 공개 키 암호화 시스템 지향;

• 새로운 유형의 수학적 문제;

• 특수 장비 지원이 필요하지 않음;

• 클래식 및 양자 컴퓨팅 조건에서 안전함;

현재 5가지 주요 구성 기술 경로는 아래 그림과 같이 왼쪽부터 격자, 인코딩, 다변량, 해싱, 상동성의 다섯 가지입니다.

1. 그리드: 그리드에 있는 어려운 문제를 기준으로 합니다.

2. 인코딩: 해독 난이도 기준.

3. 다변량: 유한 필드에 대한 다변량 이차 다항식 그룹의 난이도를 기준으로 합니다.

4. 해싱: 해시 함수의 충돌 저항을 기반으로 합니다.

5. 동형성: 초단일 타원 곡선에 기반한 의사 랜덤 방황.

차세대 암호화 알고리즘에는 당연히 표준 암호화 시스템의 구축이 수반될 것입니다. 포스트 양자 암호에서 가장 주목할 만한 것 중 하나는 미국 국립표준기술연구소(NTST)의 포스트 양자 암호 표준화 프로젝트[7]로, 2016년에 시작된 이후 사실상 포스트 양자 암호 표준화 작업이 거의 마무리 단계에 이르렀습니다. 약 10년에 걸친 표준화 일정을 되돌아보면, NIST는 다음과 같이 네 가지 포스트 양자 암호 표준 후보 알고리즘을 공식 발표했습니다.

2022년 7월 5일 [8]:

• 공개 키 암호화/키 래핑: CRYSTALS-KYBER;

• 디지털 서명: CRYSTALS-Dilithium, FALCON; SPHINCS+;

이 중 CRYSTALS-KYBER, CRYSTALS-Dilithium, FALCON은 격자 암호 알고리즘이지만 세 가지의 보안 기반이 다른데, KYBER는 모달 격자의 MLWE라는 어려운 문제를 기반으로 합니다. KYBER는 모달 격자의 MLWE 난제를 기반으로 하고, 딜리튬은 모달 격자의 MLWE와 MSIS 난제를 기반으로 하며, 팔콘은 NTRU 격자의 SIS 난제를 기반으로 하고, 그 외에 SPHINCS+는 상태 비저장 해시 서명 알고리즘을 기반으로 합니다.

2023년 8월 24일, CRYSTALS-KYBER, CRYSTALS-Dilithium, SPHINCS+는 각각 FIPS203, FIPS 204, FIPS205 표준 초안으로 구성되었으며[9], 2024년에 FALCON 표준 초안도 발표될 예정입니다. FIPS203, FIPS 204, FIPS205 [9] 및 FALCON 표준은 2024년에 발표될 예정입니다.

NIST가 선택한 대부분의 표준 알고리즘이 격자 암호 기술 경로를 기반으로 한다는 것을 쉽게 알 수 있습니다. 그러나 NIST는 모든 계란을 한 바구니에 담지 않고 격자 구조 이외의 다양한 옵션을 적극적으로 추구하고 있습니다. 2022년 4개의 표준 알고리즘 발표와 동시에 공개 키 암호화/키 래핑 알고리즘에 초점을 맞춘 4차 포스트 양자 암호 표준 알고리즘 평가를 시작한다고 발표했으며, 선정된 알고리즘은 격자 구조에 기반하지 않은 알고리즘이었습니다. 또한, 4차 평가와는 별개로 디지털 서명 알고리즘에 대한 새로운 공모를 시작했으며, 포스트 양자 서명 알고리즘 포트폴리오를 풍부하게 하기 위해 기존 구조적 격자 기반 알고리즘과 다른 알고리즘 구성과 알고리즘 서명의 크기가 작고 검증이 빠른 새로운 제안에 더 중점을 두고 있습니다.

NIST 표준 외에도 국제 인터넷 표준화 기구 IETF는 2018년과 2019년에 각각 상태 저장 해시 서명 알고리즘인 XMSS를 RFC 8391[10]로, LMS를 RFC 8554[11]로 표준화하여 NIST의 승인을 받았습니다.

격자 암호 해독을 위한 양자 알고리즘

2024년 4월 10일, Yiran Chen의 전자 인쇄 기사 "Quantum. 격자 문제를 위한 알고리즘"[12]은 학계에 센세이션을 일으켰습니다. 이 논문은 격자 문제를 해결하기 위한 다항식 시간 양자 알고리즘을 제시했는데, 이는 격자 문제를 기반으로 하는 많은 암호화 체계에 큰 영향을 미쳤으며, 오늘날 널리 사용되는 LWE 가정에 기반한 동형 암호화 알고리즘과 같이 많은 알고리즘이 더 이상 양자 컴퓨터의 공격에 저항할 수 없게 만들 수 있습니다. 이 논문에서 사용된 알고리즘의 정확성은 아직 알려지지 않았습니다.

오데드 레게브는 논문 "격자, 오류, 랜덤 선형 코드 및 암호화에 대한 학습"[13]에서 LWE 문제의 난이도를 엄격하게 입증했습니다. 특히, 그의 논문에서 저자는 LWE 문제의 난이도를 격자상의 이산 가우시안 샘플링 문제로 일반화하여 엄격한 논증을 제시하고 있는데, 이는 GapSVP, SIVP 등과 같은 고전적인 문제로 쉽게 일반화할 수 있으며(물론 각 특정 문제에는 고유한 매개 변수가 있지만 여기서는 무시합니다), LWE 문제가 이러한 고전적인 격자 문제보다 훨씬 더 어렵다는 것을 시사하고 있습니다. LWE 문제의 난이도가 엄격하게 낮아진 후, 간단한 구조로 인해 (동형) 암호화, 서명, 키 교환 등과 같은 기본 암호화 기본 요소는 물론 ID 기반 암호화, 속성 기반 암호화 등을 기반으로 하는 고급 암호화 기본 요소를 포함하는 LWE 기반 암호화 체계가 많이 등장했으며, 그중에서 업계에서 더 널리 사용되는 암호화 체계가 있습니다. 그 중 업계에서 가장 널리 사용되는 것은 위에서 언급한 대로 NIST에서 발표한 포스트퀀텀 표준 알고리즘(KYBER, 딜리튬 등)과 완전 동형 암호에 중점을 두고 있습니다.

요약

이 논문은 공개되자 학계에 큰 반향을 일으켰고 많은 전문가 사이에서 많은 논의를 불러일으켰습니다. 그러나 논문의 이해 난이도가 매우 높아 전 세계에서 논문 내용을 완전히 이해할 수 있는 학자는 5명 미만일 수 있으며, 논문의 정확성을 완전히 검증하는 데 1~2년이 걸릴 수 있습니다. 현재 일부 포럼, 공개 웹 사이트 및 Zhihu와 같은 플랫폼의 많은 사람들이 관련 의견을 표명했지만 모두 논문의 알고리즘이 정확할 경우 영향을 분석하고 있으며 아무도 논문에서 알고리즘의 정확성에 대한 결론을 내릴 수 없습니다. 그 중 저명한 암호학자 N. P. Smart는 블로그 게시물 "제안된 양자 공격이 LWE에 미치는 영향"[14]을 통해 이 공격의 영향과 몇 가지 통찰력을 자세히 설명했는데, 이를 요약하면 다음과 같습니다.

• 이 논문은 아직 동료 검토를 거치지 않았으며, 올바른 것으로 확인되더라도 양자 컴퓨터에 의존하므로 양자 컴퓨터를 아직 사용할 수 없는 한 현재 사용 중인 어떤 암호화 체계에도 영향을 미치지 않습니다.

• 논문에서 제시된 결과에 따르면, NIST가 이전에 제시한 표준화된 알고리즘인 카이버, 딜리튬을 깨는 것은 아직 불가능하지만 NIST는 이러한 알고리즘의 파라미터를 재평가할 수 있습니다.

• BFV/CKKS/BGV와 같이 일반적으로 사용되는 RLWE 동형 암호화 알고리즘의 경우, 이러한 알고리즘은 본 백서의 공격 능력 범위 내에 있습니다. 그러나 학문적, 산업적 관점에서 볼 때 동형 암호의 '동형성'이 '양자 저항성'보다 더 매력적이며, '양자 저항성'을 추구하기 위해 RLWE 동형 암호를 사용하는 사람은 거의 없습니다. RLWE 동형 암호화는 양자 알고리즘이 오랫동안 제안되어 왔지만 학계와 업계에서 여전히 연구 및 사용되고 있는 이산 로그 문제에 의존하는 타원 곡선 기반 암호화 체계와 유사합니다.

업데이트: Chen의 논문에서 계산에 문제가 발견되어 그리드 암호 경보가 일시적으로 해제되었습니다.

[1] https:// ethresear.ch/t/how-to-hard-fork-to-save-most-users-funds-in-a-quantum-emergency/18901/9

[2] 베니오프 P. 물리 시스템으로서의 컴퓨터 : 튜링 머신으로 대표되는 컴퓨터의 미시적 양자 역학적 해밀턴 모델[J]. 통계 물리학 저널, 1980, 22: 563-591.

[3] Shor P W. 양자 계산을 위한 알고리즘: 이산. 로그와 인수분해[C]// 컴퓨터 과학의 기초에 관한 제 35 회 연례 심포지엄 프로시딩. Ieee, 1994: 124-134.

[4] Grover L K. 데이터베이스 검색을 위한 빠른 양자역학적 알고리즘[C]//Proceedings of the 28th annual ACM symposium on Theory of. 1996: 212-219.

[5] Bernstein, D.J. (2009). 양자 이후 암호화 소개. 에: Bernstein, D.J., Buchmann, J., Dahmen, E. (eds) 포스트 양자 암호학. 스프링거, 베를린. 하이델베르크.

[6] Gisin N, Ribordy G, Tittel W, 외. 양자 암호학[J]. 리뷰 오브 모던 피직스, 2002, 74(1): 145.

[7] https://csrc.nist.gov/Projects/post-quantum- 암호학/양자 암호 표준화

[8] https://csrc.nist.gov/News/ 2022/pqc-candidates-to-be-standardised-and-round-4

[9] https://csrc.nist.gov/News/2023 /three-draft-fips-for-post-quantum-cryptography

[10] Huelsing, A., Butin, D., Gazdag, S., Rijneveld, J.. , 및 A. Mohaisen, "XMSS: 확장 머클 서명 체계", RFC 8391, DOI 10.17487/RFC8391, May 2018, <https://www.rfc-editor.org/info/ rfc8391>.

[11] McGrew, D., Curcio, M., and S. Fluhrer, "Leighton-Micali 해시 기반 서명", RFC 8554, DOI 10.17487/. RFC 8554, 4월 2019, <https://www.rfc-editor.org/info/rfc8554>.

[12] Chen Y. 격자 문제를 위한 양자 알고리즘[J]. 암호학 전자 인쇄 아카이브, 2024.

[13] 레게브 O. 격자, 오류, 랜덤 선형 코드로 학습. 암호화[J]. 2009, 56(6): 1-40.

[14] https://nigelsmart.github.io/LWE.html

< /blockquote>

 이 글은 ZAN 팀의 동니와 지아싱이 공동 집필했습니다(X 계정 @zan_team).