Glassnode: How does coin age affect Bitcoin’s buying and selling patterns?

Author: Mario Schröck, Glassnode; Translator: Tao Zhu, Golden Finance

Foreword

Bitcoin’s transparent blockchain allows for detailed analysis of token movement and holder behavior. By examining the age of unspent transaction outputs (UTXOs) and their spend probability, we can gain insight into the dynamics of the Bitcoin ecosystem. This paper explores the power-law relationship between UTXO age and buy-sell probability, revealing predictable patterns in how tokens are held and bought and sold over time.

Why this analysis is important

Understanding Bitcoin’s UTXO spending behavior provides powerful insights for traders, investors, and analysts alike. By revealing predictable patterns that control currency dormancy, you can:

• Enhance investment strategies:Predict potential liquidity changes and better gauge market sentiment.

• Improving on-chain analysis:Leveraging a mathematical framework to complement traditional LTH/STH indicators.

• Predicting holder behavior:Determine when a token is likely to re-enter circulation, informing the timing of transactions or decisions.

Whether you are optimizing a trading algorithm, analyzing market trends, or refining an investment approach, this framework can give you a clear, data-driven edge in the Bitcoin ecosystem.

What are UTXOs and Spending Probability?

At the heart of the Bitcoin blockchain is the UTXO model. UTXO stands for Unspent Transaction Output - essentially a block of Bitcoin that has been received but not yet spent. Every Bitcoin transaction consumes existing UTXOs as inputs and creates new UTXOs as outputs. These UTXOs can be thought of as tokens sitting at a specific address, waiting to be spent in a future transaction.

By analyzing the age (number of days since creation) of these UTXOs, we can infer behavioral patterns of holders in the network. A fundamental concept in this analysis is the spend probability, which measures the likelihood that a UTXO at a given time will be spent on any given day. This metric quantifies how Bitcoin moves within the ecosystem and how holder behavior evolves.

Methodology

Dataset and UTXO Counts

Our analysis is based on Bitcoin UTXO data from 2015 to November 2024. For each day during this period, we count the number of UTXOs of each possible coin age, from one day to 10 years (approximately 3,650 days). We cap the maximum coin age at 10 years to avoid the noise inherent in extremely old UTXO data.

Calculating Spending Rates

To determine spend probability, we compare the number of UTXOs of a particular coin age on one day to the number of UTXOs of the next higher coin age on the next day. The consumption part is calculated as follows:

Spending fraction = 1 - (number of UTXOs with age N in T days) / (number of UTXOs with age N-1 in T-1 days)

This formula represents the fraction of UTXOs with age N-1 that do not appear as UTXOs with age N on the next day, which means they have been spent.

We then calculate the average spending rate for each age group across the entire dataset, as well as the standard error of the mean. Figure 1 visually shows the average spending rate by coin age.

Power-Law Dynamics in Log-Log Space

To better understand the relationship between UTXO coin age and spending rate, we plotted the data in log space. This transformation is beneficial because the power-law relationship appears as a straight line in double-log space, making it easier to identify and analyze. Figure 2 shows a double-log plot of the spending rate.

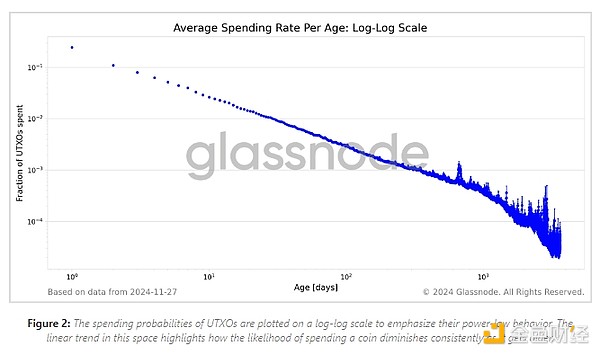
Fitting the Power Law

We perform linear regression on the double-log data to quantify the power-law relationship. We use weighted least squares for regression, with weights proportional to the square of the UTXO count divided by the square of the standard error of the mean. This weighting takes into account the variation in the reliability of the data points due to different sample sizes and variances.

The slope of the regression line corresponds to the power-law exponent, indicating how fast the probability of consumption decreases with age. Figure 3 shows the fitted regression.

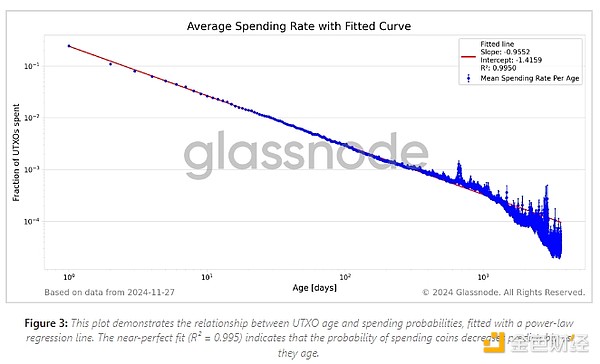
Analyzing residuals to assess fit quality

To assess the fit quality of the power law across different coin age groups, we analyzed the residuals, i.e., the difference between the observed average spending rate and the value predicted by our model. Plotting the residuals helps us identify patterns or systematic deviations from the model. Figure 4 shows the residuals as a function of UTXO coin age.

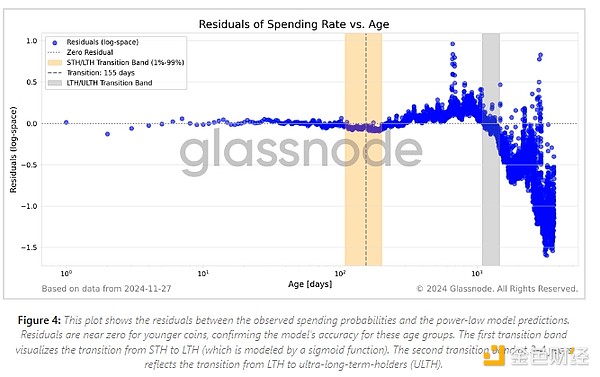
We observe minimal residuals for UTXOs around 200 days, indicating that the cohort is highly predictable. This is consistent with a gradual transition from short-term holders (STHs) to long-term holders (LTHs). The S-shaped function models this transition to obtain a smooth transition in holder behavior. The center point of this transition is the 155-day mark, representing a 50-50 split between STH and LTH classifications. At around 200 days, the conversion from STH to LTH is 99% complete.

Our analysis shows that the power-law model fits STH tokens almost perfectly until they fully transition to LTH. For LTH tokens with a coin age of 3-4 years (the second transition band), the model remains well-behaved (with small deviations). These deviations suggest that the medium-term LTH cohort has slightly higher spend probabilities than the model predicts.

However, for ultra-long-term holders (ULTH) — tokens that have been around for more than about one halving cycle — we observe more significant deviations from the model. Specifically, the observed spend probabilities are lower than those predicted by the power-law. This suggests a greater propensity to hold onto these tokens, perhaps due to a strong holding conviction or the possibility that some of them are lost.

Power-law over time

We examine whether the power-law dynamics of token spend probabilities change over time from another perspective. Instead of averaging the UTXO counts for each coin age across all dates, we track groups of UTXOs born on the same day. Based on these date groups, we can analyze how the spend rates of tokens at different times in Bitcoin’s history evolve.

For each cohort, we calculated the spending rate on a daily basis as the age of the cohort increased. We then performed a linear regression on the double log probability of spending for each cohort separately. Ignoring the most recently recorded cohort with a survival time of less than 10 days resulted in approximately 3600 remaining cohorts and corresponding linear regressions.

The coefficient of determination (R2) for each regression indicates how well the power law model fits the data for that cohort. The slope of each line gives us an idea of ​​how quickly the spending rate decreases as the coin age increases. Figure 5 plots the R2 value and line slope for each date cohort over time.

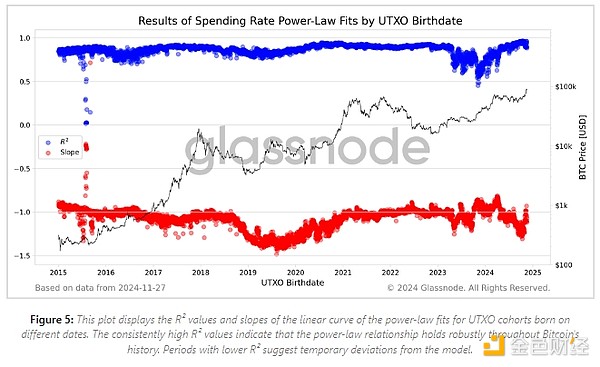
Overall, the power law fits well across different dates, confirming the consistency of this dynamic over time. However, specific periods show lower quality of fit, although there is no clear correlation with price movements during these periods. We observe an early extension of the probability of spending (smaller slope values) throughout 2019. One possible explanation is that investors who bought at the time of the -80% drop from the 2017 ATH were investing for the long term, and therefore, had higher spending rates than in general.

Implications for On-Chain Analysis

These findings provide a consistent perspective on coin age and spending probability, complementing the existing LTH/STH framework. The power-law relationship captures the gradual shift from active trading to long-term holding.

Notably, the model fits younger coins almost perfectly and remains good (with only minor deviations) for coins with a coin age of around four years. Beyond this age, the deviations from the model become more significant, suggesting that other factors may influence the spending behavior of very long-term holders.

A power law with a slope close to 1 provides a clear and intuitive rule of thumb: for every tenfold increase in the lifespan of a coin, its probability of being spent decreases by approximately tenfold. This is illustrated by the approximate model values ​​in the table below:

This predictable decay in spend probability highlights a behavioral pattern where younger tokens are actively traded or speculated, while older tokens become increasingly dormant over time.By adopting this ongoing perspective, analysts and investors gain a richer understanding of the gradual decline in spend activity as tokens age, enhancing the interpretation of on-chain data and investor behavior.

Quantifying the Hot Supply Hypothesis

Based on our data, we evaluated a simple prediction heuristic:

If a UTXO is less than 7 days old, assume that the UTXO will be spent that day. Otherwise, assume that it will not be spent.

Using historical data, this heuristic is 98% accurate, indicating that it correctly predicts whether a UTXO will be spent in the vast majority of cases. However, due to the imbalance of the dataset, the high accuracy numbers can be somewhat misleading - there are a large number of unspent UTXOs on any given day.

Conclusion

Our analysis shows that Bitcoin UTXO spending behavior is governed by a strong power-law dynamic, with older coins becoming progressively less likely to be spent. The power-law relationship fits younger coins almost perfectly, and remains well for coins up to four years old (with only minor deviations). For ultra-long-term holders beyond this coin age, deviations from the model become more pronounced, indicating that the spend probability is even lower than the model predicts. This suggests that other factors, such as strong holding conviction or lost tokens, influence the spending behavior of these oldest UTXOs.

This finding enhances the existing LTH/STH framework by providing a sequential mathematical perspective on the gradual shift from active transactions to long-term holding. The power law provides a precise rule of thumb: for every tenfold increase in the lifespan of a coin, its probability of being spent decreases by approximately tenfold. This predictable decay in spend probability provides valuable insights into investor behavior and coin dormancy over time.

As Bitcoin continues to evolve, the power law model provides a mathematically grounded framework for on-chain analysis, enabling a deeper understanding of the UTXO lifecycle dynamics.