The quantum crisis of lattice cryptography? An article explains the academic controversy over lattice cryptography

Quantum security threats and responses to blockchain

On March 10, 2024, Ethereum co-founder Vitalik Buterin published a new article titled "How to hard-fork to save most user's funds in a quantum emergency"[1] on the Ethereum Research Forum (ethresear.ch). The article states that the threat of quantum computing attacks faced by the Ethereum ecosystem can be protected by restorative fork strategies and quantum-resistant cryptographic technology.

What exactly is the quantum security threat to blockchain?

Quantum computing[2] was proposed in the 1980s as a new computing model that uses quantum mechanics to control quantum information units for computing. In the decade after its concept was proposed, quantum computers remained at the abstract theoretical stage. It was not until the mid-1990s that two quantum algorithms were proposed: Shor's algorithm [3] (which solves the problem of large number decomposition and discrete logarithm difficulty in polynomial time) and Grover's algorithm [4] (which provides quadratic acceleration for the exhaustive search problem of unstructured data), that quantum computing jumped out of the abstract theoretical stage and entered a new stage of physical carrier research and development, which is now called quantum computers. The figure below shows the development roadmap of physical quantum bits of quantum computers from 1998 to 2026:

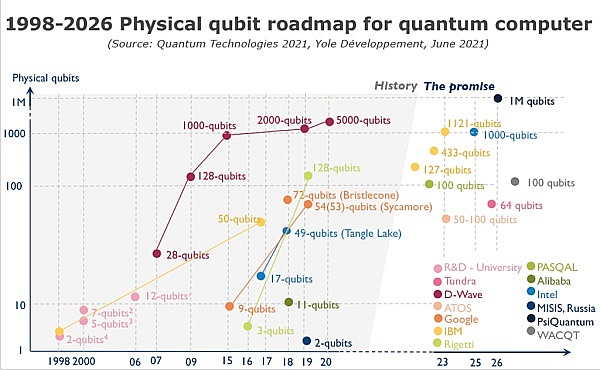
Quantum computing is not omnipotent and cannot solve all computing problems. At present, it can play its computing superiority in specific fields such as simulation (simulating the process of nature, applicable to chemical and biological engineering), decryption (breaking most traditional cryptographic systems, applicable to network security), optimization (finding the optimal solution among feasible options, applicable to finance and supply chain).

The widespread application of blockchain currently comes from the new trust foundation it brings to the collaboration between different parties, and this trust foundation is built on the security guarantee provided by the underlying cryptography:

• Trusted identity and transaction confirmation: Establish user trusted identity based on asymmetric public and private key pairs, and uniformly manage identity information. The confirmation of digital assets is achieved through digital signatures, and the private key holder with valid signature actually owns the asset ownership.

• Core consensus and operational security: Construct a consensus mechanism based on modern cryptographic technologies such as hash functions, threshold signatures, and verifiable random functions to ensure the security of the consensus mechanism.

• Privacy protection and secure sharing: Based on zero-knowledge proof, secure multi-party computing, fully homomorphic and other rich-function cryptographic technologies, a privacy protection scheme is built to achieve secure sharing of data on the blockchain.

• Controllable supervision and compliance application: Integrate and deploy cryptographic technologies such as ring signatures, homomorphic cryptographic schemes, hidden addresses and secret sharing to ensure secure supervision of blockchain transactions.

The use of public key cryptography can be roughly divided into: digital signature mechanism used for tamper-proof transactions on the chain, and secure transmission protocol used for communication between nodes. Affected by Shor's algorithm, the security of the above public key cryptography cannot be effectively guaranteed in use. While considering the time required for large-scale application of quantum computers to decipher special passwords, it is also necessary to consider how long the data stored on the blockchain needs to be saved and the time it takes for the existing blockchain system to be upgraded to the quantum security level. If the sum of the time of the latter two is greater than the former, the data on the blockchain will be seriously threatened by quantum computing.

Considering the current situation of the continuous improvement of computing power brought about by the rapid development of quantum computing, there are currently two main technical approaches that can effectively deal with security risks:

1. Post-quantum cryptography based on new mathematical problems without the help of physical equipment[5] Technical route;

2. Quantum cryptography based on physical principles with the help of special physical equipment[6] Technical route.

Taking into account various factors such as implementation verification, in order to ensure the security of blockchain in the long-term evolution, on the premise of being compatible with existing cryptographic security, it is possible to consider upgrading the blockchain to quantum security level through post-quantum cryptographic migration in advance. Ideally, upgrading the public key cryptography algorithm used in the existing blockchain to a quantum-safe post-quantum cryptography algorithm should meet the following characteristics as much as possible:

• Small keys and short signatures: Every transaction on the blockchain will contain signature information, and the public key to verify any transaction is also stored on the chain. If the key and signature size are too large, the storage cost and communication overhead of the blockchain will be greatly increased;

• High computational efficiency: The number of transactions that can be processed in each time period when the blockchain is running is largely related to the running time of the algorithm, especially the signature verification algorithm. Faster computational efficiency of the algorithm can better support high-performance blockchain applications.

Current Development Status of Post-Quantum Cryptography

Post-quantum cryptography, in a nutshell, is the first generation of cryptographic algorithms that can resist attacks by quantum computers on existing cryptographic algorithms:

• Oriented to public key cryptography system;

• Rely on new mathematical problems;

• Does not require special equipment support;

• Safe under classical computing and quantum computing conditions;

There are currently five mainstream construction technology routes, as shown in the figure below, from left to right are lattice, encoding, multivariate, hashing and homology:

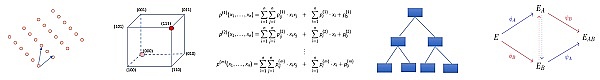
1. Lattice: Based on the difficult problem on the lattice.

2. Encoding: Based on the difficulty of decoding.

3. Multivariate: Based on the intractability of multivariate quadratic polynomial groups over finite fields.

4. Hash: Based on the anti-collision property of hash functions.

5. Homology: Based on pseudo-random walks on supersingular elliptic curves.

The new generation of cryptographic algorithms will certainly involve the establishment of a standard cryptographic system. The most noteworthy post-quantum cryptographic standardization project [7] of the National Institute of Standards and Technology (NTST) of the United States has basically entered the final stage of the formulation of post-quantum cryptographic standardization since its launch in 2016. Looking back at the nearly ten-year standardization timeline, NIST: On July 5, 2022, it officially announced four candidate algorithms for post-quantum cryptography standards [8]: Public key encryption/key encapsulation: CRYSTALS-KYBER; Digital signature: CRYSTALS-Dilithium, FALCON; SPHINCS+; Among them, CRYSTALS-KYBER, CRYSTALS-Dilithium, and FALCON are all lattice cryptographic algorithms, but their security foundations are different. KYBER is based on the MLWE difficulty problem of modular lattices, Dilithium is based on the MLWE and MSIS difficulty problems of modular lattices, and FALCON is based on the SIS difficulty problem of NTRU lattices. In addition, SPHINCS+ It is a stateless hash signature algorithm.

On August 24, 2023, CRYSTALS-KYBER, CRYSTALS-Dilithium, and SPHINCS+ were respectively formed into FIPS203, FIPS 204, and FIPS205 draft standards [9], and the FALCON draft standard will also be announced in 2024.

It is not difficult to see that the standard algorithms currently selected by NIST are mostly based on the technical route of lattice cryptography. However, NIST does not put all its eggs in one basket. They are also actively seeking multiple options besides lattice construction: while announcing four standard algorithms in 2022, they also announced the launch of the fourth round of post-quantum cryptography standard algorithm evaluation work. This round focuses on public key encryption/key encapsulation algorithms, and the selected algorithms are not based on lattice construction. In addition, a new round of solicitation for digital signature algorithms was launched. This round of solicitation was conducted independently from the fourth round of evaluation. It aims to enrich the post-quantum signature algorithm portfolio, so it focuses more on new proposals that are different from the existing structural lattice-based algorithm in terms of algorithm construction, and have small algorithm signature size and fast verification speed.

In addition to the NIST standard, the International Internet Standards Organization IETF standardized the stateful hash signature algorithm XMSS as RFC 8391[10] and LMS as RFC 8554[11] in 2018 and 2019 respectively, and they were accepted by NIST.

Quantum Algorithms for Cracking Lattice Cryptography

On April 10, 2024, Professor Chen Yilai's article "Quantum Algorithms for Lattice Problems"[12] on eprint caused a sensation in the academic community. The paper presents a quantum algorithm that solves the lattice-based hard problem in polynomial time. This algorithm has a significant impact on many cryptographic schemes based on the lattice-based hard problem, and may cause many algorithms to no longer be able to resist quantum computer attacks, such as the widely used homomorphic encryption algorithm based on the LWE assumption. The correctness of the algorithm in the paper is not yet known. The difficulty of the LWE problem was rigorously demonstrated by Oded Regev in his paper "On lattices, learning with errors, random linear codes, and cryptography" [13]. Specifically, the author reduces the difficulty of the LWE problem to the discrete Gaussian sampling problem on the lattice in the paper, and the discrete Gaussian sampling problem can be easily reduced to classic problems such as GapSVP and SIVP (of course, each specific problem has its own specific parameters, which are ignored here). This shows that the LWE problem is more difficult than these classic lattice problems. After the difficulty of the LWE problem has been strictly reduced, a large number of cryptographic schemes based on LWE have emerged due to its simple structure, covering basic cryptographic primitives such as (homomorphic) encryption, signature, key exchange, and advanced cryptographic primitives such as identity-based encryption and attribute encryption. Among them, the most widely used in the industry are fully homomorphic encryption and the post-quantum standard algorithms (KYBER, Dilithium, etc.) announced by NIST mentioned above.

Summary

After the paper was made public, it caused a great sensation in the academic community and aroused discussions among many professionals. However, since the paper is extremely difficult to understand, there may be less than 5 scholars in the world who can fully understand the content of the paper, and it may take 1-2 years to fully verify the correctness of the paper. At present, many people have expressed some relevant opinions on some forums, public accounts, Zhihu and other platforms. Everyone is analyzing what impact will be brought if the algorithm in the paper is correct. As for the correctness of the algorithm in the paper, no one has yet come to a conclusion. Among them, the famous cryptographer N. P. Smart published a blog post "Implications of the Proposed Quantum Attack on LWE" [14], which details the impact of this attack and some opinions. The summary is as follows:

• This paper has not yet been peer-reviewed. Even if it is verified to be correct, it still depends on quantum computers. Therefore, as long as quantum computers have not yet been released, it will have no impact on the cryptographic schemes currently in use.

• According to the results given in the paper: it is still impossible to break the standardized algorithms Kyber and Dilithium given by NIST, but NIST may re-evaluate the parameters of these algorithms.

• For commonly used RLWE homomorphic encryption algorithms, such as BFV/CKKS/BGV, these algorithms are within the attack capabilities of this paper. However, whether from the perspective of academia or industry, the "homomorphism" of homomorphic encryption technology is more attractive than its "quantum resistance". Few people will use RLWE homomorphic encryption algorithms in pursuit of "quantum resistance", just like the cryptographic scheme based on elliptic curves relies on the discrete logarithm problem, and the quantum algorithm for solving this problem has been proposed a long time ago, but academia and industry are still studying and using these schemes.

Latest news: There are problems with the calculation of Professor Chen's paper, and the lattice password alarm is temporarily lifted. [1] https://ethresear.ch/t/how-to-hard-fork-to-save-most-users-funds-in-a-quantum-emergency/18901/9 [2] Benioff P. The computer as a physical system: A microscopic quantum mechanical Hamiltonian model of computers as represented by Turing machines[J]. Journal of statistical physics, 1980, 22: 563-591. [3] Shor P W. Algorithms for quantum computation: discrete logarithms and factoring[C]//Proceedings 35th annual symposium on foundations of computer science. Ieee, 1994: 124-134.

[4] Grover L K. A fast quantum mechanical algorithm for database search[C]//Proceedings of the twenty-eighth annual ACM symposium on Theory of computing. 1996: 212-219.

[5] Bernstein, D.J. (2009). Introduction to post-quantum cryptography. In: Bernstein, D.J., Buchmann, J., Dahmen, E. (eds) Post-Quantum Cryptography. Springer, Berlin, Heidelberg.

[6] Gisin N, Ribordy G, Tittel W, et al. Quantum cryptography[J]. Reviews of modern physics, 2002, 74(1): 145.

[7] https://csrc.nist.gov/Projects/post-quantum-cryptography/post-quantum-cryptography-standardization

[8] https://csrc.nist.gov/News/2022/pqc-candidates-to-be-standardized-and-round-4

[9] https://csrc.nist.gov/News/2023/three-draft-fips-for-post-quantum-cryptography

[10] Huelsing, A., Butin, D., Gazdag, S., Rijneveld, J., and A. Mohaisen, "XMSS: eXtended Merkle Signature Scheme", RFC 8391, DOI 10.17487/RFC8391, May 2018, <https://www.rfc-editor.org/info/rfc8391>.

[11] McGrew, D., Curcio, M., and S. Fluhrer, "Leighton-Micali Hash-Based Signatures", RFC 8554, DOI 10.17487/RFC8554, April 2019, <https://www.rfc-editor.org/info/rfc8554>.

[12] Chen Y. Quantum Algorithms for Lattice Problems[J]. Cryptology ePrint Archive, 2024.

[13] Regev O. On lattices, learning with errors, random linear codes, and cryptography[J]. Journal of the ACM (JACM), 2009, 56(6): 1-40.

[14] https://nigelsmart.github.io/LWE.html

 This article was co-authored by Dongni and Jiaxing from ZAN Team (X account @zan_team).