Author: Vitalik Buterin, Translator: Kurt Pan, XPTY
This article assumes that you are familiar with the basics of how SNARK and STARK work; if you are not familiar, it is recommended to read the first few sections of this article. Special thanks to Eli ben-Sasson, Shahar Papini, Avihu Levy, and others at starkware for their feedback and discussions.

This transformation This has resulted in significant improvements in proof speed, most notably Starkware's ability to prove 620,000 Poseidon2 hashes per second on an M3 laptop. Specifically this means that as long as we are willing to trust Poseidon2 as part of the hash function, one of the most difficult parts of building an efficient ZK-EVM has been efficiently solved. But how do these techniques work, and how are cryptographic proofs (which often require large integers for security) built on these domains? And how do these protocols compare to more exotic constructs like Binius? This article will explore some of the subtle differences, focusing specifically on a construct called Circle STARKs (implemented in Starkware's stwo, Polygon's plonky3, and my own python implementation), which have some unique properties designed to Compatible with the efficient Mersenne31 domain.
https://x.com/StarkWareLtd/status/1807776563188162562
< /li>https://vitalik.eth.limo/general/2022/08/04/zkevm.html
https://vitalik.eth.limo/general/2024/04/29/binius.html
https://www.irreducible.com/posts/binius-hardware-optimized-snark
https://eprint.iacr.org/2024/278
https://github.com/starkware-libs /stwo
https://github.com/Plonky3/Plonky3
https://github.com/ethereum/research/tree/master/circlestark
Common problems in small domains h2>
One of the most important "tricks" when doing hash-based proofs (or indeed any kind of proof) is to prove something about the evaluation of the polynomial at random points instead of proving something about the underlying polynomial .

- https://en.wikipedia.org/wiki/Fiat%E2%80%93Shamir_heuristic

There are two natural solutions to this problem:
- Execute Multiple random tests
 < /p>
< /p>
- https://www2.clarku.edu/faculty/djoyce/complex/mult.html

The implementation here is not optimal (it can be optimized with Karatsuba), it just shows the principle

< h2>Regular FRI


- https://eccc.weizmann.ac.il/report /2017/134/



Circle FRI

- https://elibensasson.blog/why-im-excited-by-circle-stark-and-stwo/
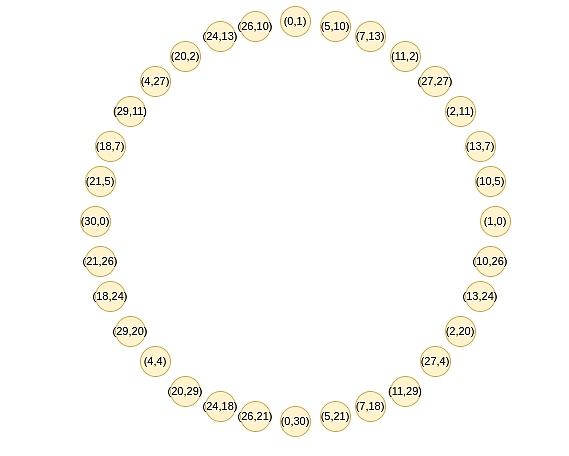
These Dots follow the law of addition, and if you've studied trigonometry or complex multiplication recently, you may find this law familiar:
- https://unacademy.com/content/cbse-class-11/study -material/mathematics/algebra-of-complex-numbers-multiplication/

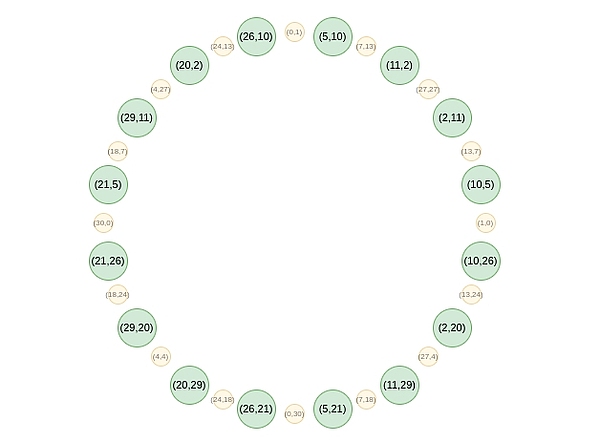

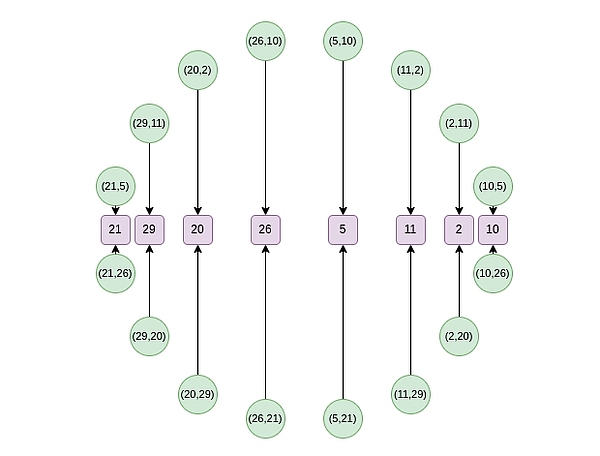
From the second round onwards, the mapping changes:

Circle FFTs

- https://vitalik.eth.limo/general/2019/05/12/fft.html< section>


- https:/ /www.researchgate.net/publication/353344649_Elliptic_Curve_Fast_Fourier_Transform_ECFFT_Part_I_Fast_Polynomial_Algorithms_over_all_Finite_Fields
From here, let’s get into some more esoteric details, for those who implement circle STARK, vs. conventional These details will be different compared to STARK.
Get business

- https:/ /eprint.iacr.org/2019/336


Vanishing Polynomial

Reverse bit order



Efficiency

Therefore, circle STARK is actually very close to optimal! Binius is even more powerful as it allows mixing and matching domains of different sizes, giving more efficient bit packing for everything. Binius also provides the option to perform 32-bit additions without the overhead of a lookup table. However, these gains come at the cost of (in my opinion) significantly higher theoretical complexity, whereas circle STARK (and regular STARK based on BabyBear) are conceptually quite simple.
Conclusion: What do I think about circle STARKs?
Compared with regular STARK, Circle STARK does not bring much additional complexity to developers. During the implementation process, the above three issues are basically the only differences I see compared to conventional FRI. The math behind the "polynomials" that Circle FRI operates on is quite counter-intuitive and takes a while to understand and appreciate. But it happens that this complexity is hidden so that developers don't see too much of it. The complexity of Circle mathematics is encapsulated, not systematic.
Understanding circle FRI and circle FFT is also a good intellectual approach to understanding other "exotic FFTs": the most noteworthy is a binary domain FFT, previously used in Binius and LibSTARK, as well as more bizarre constructs, such as the elliptic curve FFT, which uses several to one mappings and works well with elliptic curve point operations.
https://github.com/ethereum/research/blob/master/binius/ binary_ntt.py#L60
https://github.com/elibensasson/libSTARK
https://arxiv.org/abs/2107.08473
By combining Mersenne31, BabyBear and binary domain technology such as Binius, we do feel that we are approaching the limits of STARK's "base layer" efficiency. At this point in time, I expect the frontier of STARK optimization to shift towards the most efficient arithmeticization of primitives like hash functions and signatures (and optimizing those primitives themselves for this purpose), recursive constructions to unlock more parallelization, Arithmetize virtual machines to improve developer experience, and other high-level tasks.
 JinseFinance
JinseFinance




 < /p>
< /p>






























