Author: Vitalik, founder of Ethereum; Translator: Deng Tong, Golden Finance
Note: This article is the sixth part of the series of articles recently published by Vitalik, founder of Ethereum, on “The Future Development of the Ethereum Protocol”, “Possible futures of the Ethereum protocol, part 6: The Splurge”. For the fifth part, see “Vitalik: The Possible Future of Ethereum Protocol—The Purge” and for the fourth part, see “Vitalik: The Future of Ethereum The Verge”. For the third part, see "Vitalik: Key Goals of Ethereum's Scourge Phase", for the second part, see "Vitalik: How Should Ethereum Protocol Develop in the Surge Phase", for the first part, see "What Other Improvements Can be Made in Ethereum PoS"". The following is the full text of Part 6:
Special thanks to Justin Drake and Tim Beiko for their feedback and comments.
Some things are hard to put into a category. There are a lot of "little things" in Ethereum protocol design that are very valuable to Ethereum's success, but don't fit into larger subcategories. In fact, about half of them end up being related to various EVM improvements, and the rest are made up of various niche topics. This is the purpose of "the Splurge".
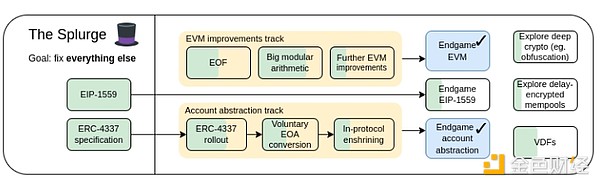
Splurge, 2023 Roadmap
The Splurge: Main Goals
Bringing the EVM to a high-performance and stable "final state"
Introduce account abstraction to the protocol so that all users benefit from safer, more convenient accounts
Optimize transaction fee economics to improve scalability while reducing risk
Explore advanced cryptography that can make Ethereum better in the long term
EVM Improvements
What Problem Does It Solve?
Today’s EVM is difficult to statically analyze, making it difficult to create efficient implementations, formally verify code, and further extend over time. Additionally, it is very inefficient, making it difficult to implement many forms of advanced cryptography unless they are explicitly supported via precompilation.
What is it and how does it work?
The first step in the current EVM improvement roadmap is the EVM Object Format (EOF), planned for inclusion in the next hard fork. EOF is a series of EIPs that specify a new version of the EVM code with a number of unique features, most notably:
Separation between code (executable, but not readable from the EVM) and data (readable, but not executable).
Dynamic jumps are prohibited, only static jumps are allowed.
EVM code can no longer observe gas-related information.
A new explicit subroutine mechanism has been added.

Structure of EOF Code
Old-style contracts will continue to exist and can be created, although they may eventually be deprecated (perhaps even forced to convert them to EOF code). New-style contracts will benefit from the efficiency gains brought by EOF - first, slightly smaller bytecode by leveraging subroutine functions, then new EOF-specific functions, or reduced EOF-specific gas costs.
After the introduction of EOF, it becomes easier to introduce further upgrades. The most complete one currently is the EVM Modular Arithmetic Extension (EVM-MAX). EVM-MAX creates a new set of operations designed for modular arithmetic and puts them into a new memory space that is not accessible through other opcodes. This allows for optimizations such as Montgomery multiplication.
A newer idea is to combine EVM-MAX with Single Instruction Multiple Data (SIMD) capabilities. SIMD has been an idea in Ethereum since Greg Colvin's EIP-616. SIMD can be used to accelerate many forms of cryptography, including hash functions, 32-bit STARKs, and lattice-based cryptography. EVM-MAX and SIMD together form a pair of performance-oriented extensions to the EVM.
The approximate design of the combined EIP is to start with EIP-6690, and then:
Allow (i) any odd number or (ii) any power of 2 (up to 2^768) as the modulus
For each EVMMAX opcode (add, sub, mul), add a version that takes 7 immediate values instead of 3 x, y, z: x_start, x_skip, y_start, y_skip, z_start, z_skip, count. In Python code, these opcodes will do the equivalent of the following:

Except in a real implementation, it will be processed in parallel.
Add XOR, AND, OR, NOT, and SHIFT (both looping and non-looping) for at least modulos of powers of 2, if possible. Also add ISZERO (push output to the EVM main stack).
This will be powerful enough to implement elliptic curve cryptography, small domain cryptography (e.g. Poseidon, round STARKs), traditional hash functions (e.g. SHA256, KECCAK, BLAKE), and lattice-based cryptography.
Other EVM upgrades may also be possible, but they have received less attention so far.
What research is there?
EOF: https://evmobjectformat.org/
EVM-MAX: https://eips.ethereum.org/EIPS/eip-6690
SIMD: https://eips.ethereum.org/EIPS/eip-616
What’s left to do, and what are the tradeoffs?
Currently, EOF is scheduled to be included in the next hard fork. While it’s always possible to remove it — features have been removed at the last minute in previous hard forks — doing so would be an uphill battle. Removing EOF would mean that any future upgrades to the EVM could not use EOF, which could be done, but would likely be more difficult.
The main tradeoff for the EVM is L1 complexity vs. infrastructure complexity. EOF is a large amount of code added to the EVM implementation, and static code inspection is quite complex. However, in exchange, we gain simplification of the high-level language, simplification of the EVM implementation, and other benefits. It’s fair to say that a roadmap that prioritizes continued improvement of Ethereum’s L1 will include and build on EOF.
One important piece of work will be implementing something like EVM-MAX plus SIMD and benchmarking how much gas various crypto operations require.
How does it interact with the rest of the roadmap?
L1 tweaking its EVM makes it easier for L2 to do the same. Tweaking one while the other creates some incompatibilities, which has its own drawbacks. Additionally, EVM-MAX plus SIMD could reduce the gas cost of many proof systems, allowing for a more efficient L2. It would also make it easier to remove more precompiles by replacing them with EVM code that can do the same tasks without having to take a big hit on efficiency.
Account Abstraction
What problem does it solve?
Currently, transactions can only be verified in one way: with an ECDSA signature. Initially, account abstraction was intended to go beyond this and allow the verification logic for an account to be arbitrary EVM code. This enables a range of applications:
Switching to quantum-resistant cryptography;
Rotating old keys (widely considered a recommended security practice);
Multi-signature wallets and social recovery wallets;
Signing low-value operations with one key and high-value operations with another key (or set of keys);
Allowing privacy protocols to work without relayers, greatly reducing their complexity and removing a key central dependency point.
Since account abstraction began in 2015, the goals have expanded to include a large number of "convenience goals", such as an account that doesn't have ETH but has some ERC20 being able to pay gas with that ERC20. A summary of these goals is shown in the table below:
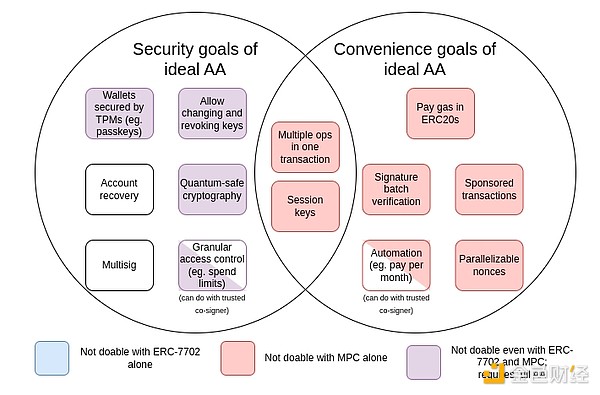
MPC here is Multi-Party Computation: a 40-year-old technique that splits a key into multiple parts, stores them on multiple devices, and uses cryptographic techniques to generate signatures without directly combining the parts of the key.
EIP-7702 is an EIP scheduled to be introduced in the next hard fork. EIP-7702 is the result of a growing recognition of the need to provide the convenience of account abstraction to all users (including EOA users) to improve everyone's user experience in the short term and avoid a split into two ecosystems. This work began with EIP-3074 and culminated in EIP-7702. EIP-7702 makes the "convenience features" of account abstraction available to all users, including EOAs (externally owned accounts, i.e. accounts controlled by ECDSA signatures).
From the diagram we can see that while some of the challenges (especially the "convenience" challenges) can be solved through multi-party computation or incremental techniques like EIP-7702, most of the security goals of the original account abstraction proposal can only be achieved by going back to the original problem: allowing smart contract code to control transaction validation. The reason this hasn't been done so far is that it's challenging to implement it securely.
What is it? How does it work?
At its core, account abstraction is simple: allow transactions to be initiated through smart contracts (not just EOAs). The entire complexity comes from doing this in a way that is conducive to maintaining a decentralized network and preventing denial of service attacks.
An illustrative example of a key challenge is the multiple invalidity problem:
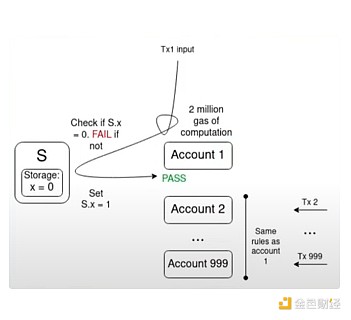
If there are 1000 accounts whose validation functions all depend on some single value S, and there are transactions in the memory pool that are valid based on the current value of S, then a transaction that flips the value of S may invalidate all other transactions in the memory pool. This allows an attacker to spam the memory pool at very low cost, clogging up the resources of network nodes.
Over the years, attempts to extend functionality while limiting DoS risks have led to a consensus on a solution for how to implement the "ideal account abstraction": ERC-4337.
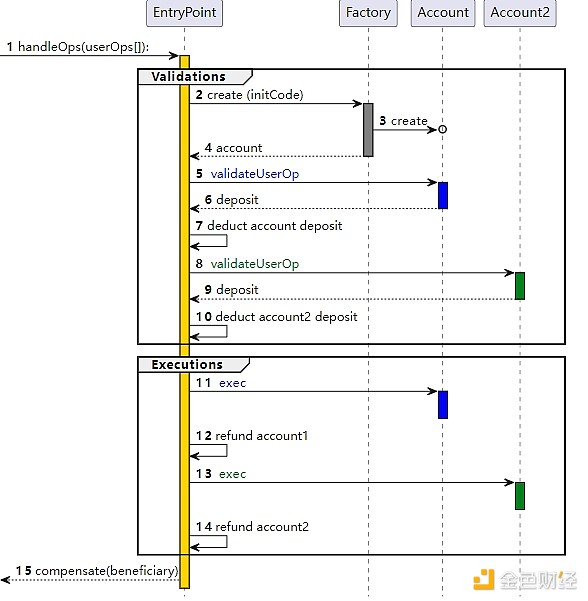
ERC-4337 works by dividing the processing of user actions into two stages: verification and execution. All verifications are processed first, and then all executions are processed. In the memory pool, user actions are accepted only if the verification phase of the user action only touches its own account and does not read environment variables. This prevents multiple invalid attacks. The verification step also enforces a strict gas limit.
ERC-4337 was designed as an out-of-protocol standard (ERC) because Ethereum client developers at the time were focused on merging and had no spare capacity to handle other functions. This is why ERC-4337 uses its own objects (called user actions) instead of regular transactions. However, recently we realized that it was necessary to incorporate at least parts of it into the protocol. Two main reasons are:
The inherent inefficiency of EntryPoint as a contract: fixed ~100k gas overhead for each package and thousands of additional fees for each user operation;
The need to ensure that Ethereum properties (such as the inclusion guarantee created by inclusion lists) carry over to users of the account abstraction.
In addition, ERC-4337 extends it with two more features:
Payers: A feature that allows one account to pay fees on behalf of another account. This violates the rule that only the sender account itself can be accessed during the verification phase, so special handling was introduced to allow the payer mechanism and ensure its security.
Aggregators: A feature that supports signature aggregation, such as BLS aggregation or SNARK-based aggregation. This is necessary to achieve maximum data efficiency in aggregation.
What research exists?
Account abstract history introduction: https://www.youtube.com/watch?v=iLf8qpOmxQc
ERC-43 37: https://eips.ethereum.org/EIPS/eip-4337
EIP-7702: https://eips.ethereum.org/EIPS/eip-7702
BLSWallet code (using aggregation): https://github.com/getwax/bls-wallet
EIP-7562 (Embedded Account Abstraction): https://eips.ethereum.org/EIPS/eip-7562
EIP-7701 (Embedded AA on EOF): https://eips.ethereum.org/EIPS/eip-7701
What's left to do, and what are the tradeoffs?
The main question left is how to fully incorporate account abstraction into the protocol. The most popular account abstraction EIP recently is EIP-7701, which implements account abstraction on top of EOF. Accounts can have a separate code section for verification, and if an account sets this code section, then the code is executed during the verification step of transactions for that account.
 EOF code structure for EIP-7701 account
EOF code structure for EIP-7701 account
The fascinating thing about this approach is that it clearly shows two equivalent ways to view the native account abstraction:
EIP-4337, but as part of the protocol
A new type of EOA where the signing algorithm is EVM code execution
If we first strictly limit the complexity of the code that can be executed during verification—— If we don't allow external state access, or even set the gas limit too low to be useful for quantum-resistant or privacy-preserving applications at first - then the security of this approach is pretty obvious: it just replaces ECDSA verification with EVM code execution that takes similar time. However, we need to relax these restrictions over time, because allowing privacy-preserving applications to work without relayers and quantum-resistance are both very important. In order to do this, we really need to find ways to address DoS risks in a more flexible way, without requiring the verification step to be extremely simple.
The main trade-off seems to be "get something that fewer people are happy with as canonical sooner" versus "wait longer and maybe get a more ideal solution". The ideal approach is probably some kind of hybrid approach. One hybrid approach is to get some use cases as canonical sooner, and leave more time to solve other use cases. Another approach is to deploy a more ambitious version of the account abstraction on L2 first. However, there is a challenge with this, that for an L2 team willing to work on adopting a proposal, they need to be convinced that L1 and/or other L2s will adopt something compatible later.
Another application we need to consider explicitly is keystore accounts, which store account-related state on L1 or a dedicated L2, but can be used on L1 and any compatible L2. Doing this efficiently will likely require L2 to support opcodes such as L1SLOAD or REMOTESTATICCALL, though it will also require an account abstraction implementation on L2 to support it.
How does this interact with the rest of the roadmap?
Inclusion lists need to support account abstraction transactions. In practice, the requirements for inclusion lists and decentralized mempools end up being very similar, though inclusion lists offer slightly more flexibility. Additionally, account abstraction implementations should ideally be as consistent on L1 and L2 as possible. If in the future we expect most users to use keystore rollups, then the account abstraction design should take that into account.
EIP-1559 Improvements
What problem does it solve?
EIP-1559 was launched on Ethereum in 2021 and significantly improves the average block inclusion time.
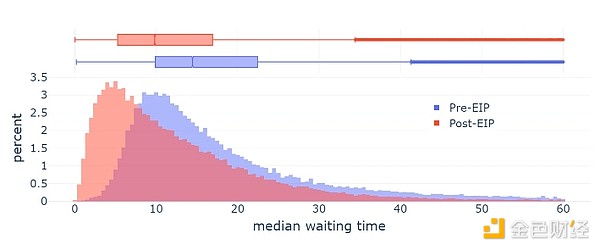
However, the current implementation of EIP-1559 is imperfect in several aspects:
The formula is slightly flawed: instead of targeting 50% of blocks, it targets ~50-53% of full blocks depending on the variance (this has to do with what mathematicians call the "AM-GM inequality");
It does not adjust fast enough under extreme conditions.
The later formula for blobs (EIP-4844) was explicitly designed to address the first problem, and is overall cleaner. Neither EIP-1559 itself nor EIP-4844 attempt to address the second. As a result, the status quo is a confusing half-way state involving two different mechanisms, and there is even a case where both need to be improved over time.
Beyond this, there are other weaknesses in Ethereum resource pricing that are unrelated to EIP-1559, but could be addressed by tweaking EIP-1559. A major issue is the difference between the average and worst cases: resource prices in Ethereum must be set to handle the worst case, where the entire gas consumption of a block takes up one resource, but the average case usage is much lower than this, resulting in inefficiencies.
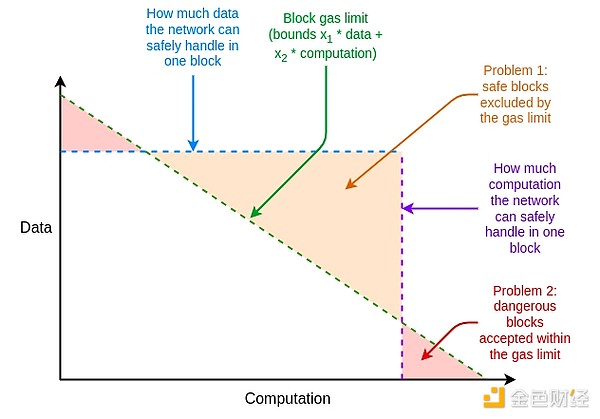
What is it? How does it work?
The solution to these inefficiencies is multi-dimensional gas: set different prices and limits on different resources. This concept is technically independent of EIP-1559, but EIP-1559 makes it easier: Without EIP-1559, optimally packing blocks with multiple resource constraints is a complex multi-dimensional knapsack problem. With EIP-1559, most blocks are not at full capacity on any resource, so a simple algorithm of "accept anything that pays enough" is sufficient.
We have multi-dimensional gas today for execution and blobs; in principle, we could increase this to more dimensions: call data, state reads/writes, and state size expansion.
EIP-7706 introduces a new gas dimension for call data. At the same time, it simplifies the multi-dimensional gas mechanism by making all three types of gas belong to a single (EIP-4844-style) framework, thus also solving the mathematical flaws of EIP-1559.
EIP-7623 is a more precise solution to the average-case vs. worst-case resource problem, which more strictly limits the maximum call data without introducing a whole new dimension.
Further directions are to solve the update rate problem and find a faster basic fee calculation algorithm while preserving the key invariants introduced by the EIP-4844 mechanism (ie: average usage is exactly close to the target in the long run).
What research is there?
EIP-1559 FAQ: https://notes.ethereum.org/@vbuterin/eip-1559-faq
EIP-1559 Empirical Analysis: https://dl.acm.org/doi/10.1145/3548606.3559341
Suggested improvements to allow for rapid adjustments: https://notes.ethereum.org/@vbuterin/proto_danksharding_faq#How-does-the-exponential-EIP-1559-blob-fee-adjustment-mechanism-work
EIP-7706: https://eips.ethereum.org/EIPS/eip-7623
Multidimensional Gas: https://vitalik.eth.limo/general/2024/05/09/multidim.html
What’s left to do, and what are the tradeoffs?
Multi-dimension gas has two main tradeoffs:
Protocol complexity is a relatively small issue for calldata, but it’s a much bigger issue for “EVM-internal” gas dimensions (e.g. storage reads and writes). The problem is that it’s not just users who set gas limits: contracts also set limits when calling other contracts. And today, the only way they can set limits is in one dimension.
A simple way to eliminate this problem is to make multi-dimensional gas only available inside EOF, since EOF does not allow contracts to set gas limits when calling other contracts. Non-EOF contracts must pay all types of gas fees when doing storage operations (e.g., if SLOAD costs 0.03% of the block storage access gas limit, non-EOF users will also be charged 0.03% of the execution gas limit)
More research on multi-dimensional gas will help understand the tradeoffs and figure out the ideal balance.
How does it interact with other parts of the roadmap?
Successful implementation of multi-dimensional gas can greatly reduce some of the "worst case" resource usage, thereby alleviating the pressure to optimize performance to support, for example, binary trees based on STARKed hashes. Setting a hard target for state size growth will make it easier for client developers to plan and estimate their future needs.
As mentioned above, due to the gas unobservability of EOF, more extreme versions of multi-dimensional gas are easier to implement.
Verifiable Delay Function (VDF)
What problem does it solve?
Today, Ethereum uses RANDAO-based randomness to select proposers. RANDAO-based randomness works by requiring each proposer to reveal a secret they committed to ahead of time, and mixing each revealed secret into the randomness. Therefore, each proposer has "1 bit of manipulation power": they can change the randomness by not showing up (for a cost). This makes sense for finding proposers, because few people can afford to give themselves two new proposals by giving up one. But for on-chain applications that need randomness, it's a no-go. Ideally, we'd find a more powerful source of randomness.
What is it? How does it work?
A Verifiable Delay Function is a function that can only be computed sequentially and cannot be accelerated by parallelization. A simple example is repeated hashing: computing i in the range (10**9): x = hash(x). The output is SNARK-proofed for correctness and can be used as a random value. The idea is that the inputs are chosen based on information available at time T, while the output is not known at time T: it is only available at some time after T, once someone has fully run the computation. Because anyone can run the computation, there is no way to withhold the result, and therefore no ability to manipulate the result.
The main risk with a verifiable delay function is accidental optimization: someone figures out how to run the function much faster than expected, allowing them to manipulate the information they reveal at time T based on future outputs. Accidental optimization can happen in two ways:
Hardware acceleration: someone builds an ASIC that runs the computation loop much faster than existing hardware.
Accidental parallelization: someone finds a way to run the function faster through parallelization, even if doing so requires 100x more resources.
The task of creating a successful VDF is to avoid both of these problems while keeping efficiency practical (e.g., one problem with hash-based approaches is that real-time SNARK proofs are hardware-intensive). Hardware acceleration is typically addressed by having public interest actors create and distribute reasonably close-to-optimal ASICs for VDFs themselves.
What research is there?
vdfresearch.org: https://vdfresearch.org/
2018 attack thoughts on the VDF used in Ethereum: https://ethresear.ch/t/verifiable-delay-functions-and-attacks/2365
Attacks on MinRoot (a proposed VDF): href="https://inria.hal.science/hal-04320126/file/minrootanalysis2023.pdf" _src="https://inria.hal.science/hal-04320126/file/minrootanalysis2023.pdf">https://inria.hal.science/hal-04320126/file/minrootanalysis2023.pdf
What’s left to do, and what are the tradeoffs?
Currently, there is no single VDF construction that fully satisfies all of Ethereum researchers’ needs. More work is needed to find such a feature. If we had it, the main tradeoff would just be whether to include it: a simple tradeoff between functionality and protocol complexity and security risk. If we believe a VDF is secure, but it turns out to be unsecure, then depending on how it is implemented, security degrades to the RANDAO assumption (1-bit manipulation per attacker) or worse. So even if the VDF is broken it won’t break the protocol, but it will break applications or any new protocol features that rely heavily on it.
How does it interact with the rest of the roadmap?
VDFs are a relatively independent component of the Ethereum protocol, but in addition to improving the security of proposer selection, they can be used for (i) on-chain applications that rely on randomness, and potentially (ii) cryptographic mempools, although making cryptographic mempools based on VDFs still relies on other cryptographic discoveries that haven’t happened yet.
One thing to keep in mind is that given the nondeterminism of the hardware, there will be some “gap” between when the VDF output is generated and when it is needed. This means that the information will be available several blocks earlier. This may be an acceptable cost, but should be considered in single-slot finality or committee selection designs, etc.
Obfuscation and One-Time Signatures: The Future of Cryptography
What Problem Does It Solve?
One of Nick Szabo’s most famous posts is a 1997 article on “The God Protocol”. In the article, he noted that multi-party applications often rely on a "trusted third party" to manage interactions. In his view, the role of cryptography is to create a simulated trusted third party to do the same job without actually requiring trust in any particular participant.
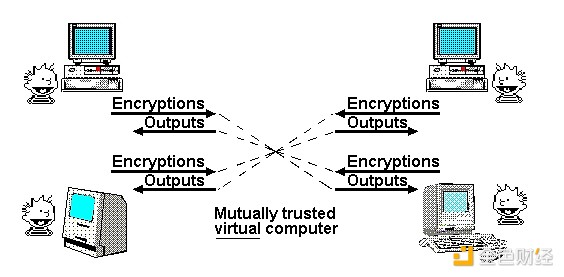
"Mathematically Trustworthy Agreement", diagram by Nick Szabo
So far, we have only partially approached this ideal. If all we need is a transparent virtual computer where data and computations cannot be shut down, censored, or tampered with, but privacy is not the goal, then blockchain can do that, albeit with limited scalability. If privacy is a goal, then until recently we’ve only been able to make a few specific protocols for specific applications: digital signatures for basic authentication, ring signatures and linkable ring signatures for primitive forms of anonymity, identity-based cryptography (which makes for more convenient cryptography under specific assumptions about trusted issuers), blind signatures for Chaumian electronic cash, and so on. This approach requires a lot of work for each new application.
In the 2010s, we first saw a different and more powerful approach based on programmable cryptography. Instead of creating a new protocol for each new application, we can add cryptographic guarantees to arbitrary programs using powerful new protocols, specifically ZK-SNARKs. ZK-SNARKs allow users to prove arbitrary statements about data they hold in a way that is (i) easily verifiable and (ii) does not reveal any data other than the statement itself. This is a huge step forward for privacy and scalability, and I liken it to the transformer effect in AI. Thousands of man-years of application-specific work were suddenly replaced by a general solution that you could just plug in to solve a staggeringly wide range of problems.
But ZK-SNARKs are just the first of three similar extremely powerful universal primitives. These protocols are so powerful that when I think about them, they remind me of a set of extremely powerful cards from Yu-Gi-Oh, a card game and TV show that I used to play and watch as a kid: the Egyptian God Cards. The Egyptian God Cards are three extremely powerful cards that, according to legend, could be fatal to craft, and so powerful that they were not allowed to be used in duels. Similarly, in cryptography, we have three Egyptian God protocols:

What is it? How does it work?
ZK-SNARKs are one of the three protocols we already have, and have reached a high level of maturity. Over the past five years, ZK-SNARKs have made huge strides in proving speed and developer friendliness, and have become a cornerstone of Ethereum's scalability and privacy strategy. But ZK-SNARKs have an important limitation: you need to know the data in order to prove it. Every state in a ZK-SNARK application must have an "owner" who must be present to approve any read or write to it.
The second protocol does not have this limitation, which is fully homomorphic encryption (FHE). FHE allows you to do any computation on encrypted data without ever seeing the data. This allows you to do computation on user data for the benefit of the user, while keeping the data and the algorithm private. It also allows you to scale voting systems like MACI to get near-perfect security and privacy guarantees. FHE was long considered too inefficient for practical use, but now it's finally become efficient enough that we're starting to see applications.
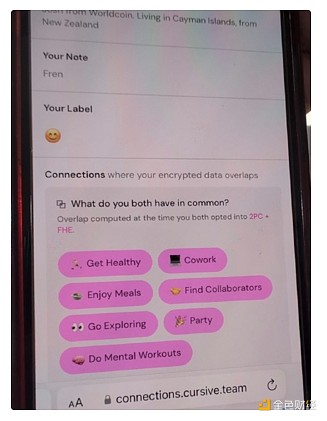
Cursive is an application that uses two-party computation and FHE for privacy-preserving discovery of common interests.
But FHE also has its limitations: any technology based on FHE still requires someone to hold the decryption key. This is possible in an M-of-N distributed setup, and you can even add a second layer of defense using a TEE, but it's still a limitation.
This brings us to the third protocol, which is stronger than the other two combined: indistinguishable obfuscation. While it's far from mature, as of 2020 we have protocols that theoretically work under standard security assumptions, and have recently started work on implementations. Indistinguishable obfuscation lets you create a "cryptographic program" that performs arbitrary computations, such that all the internal details of the program are hidden. As a simple example, you can put your private key into an obfuscated program that only allows you to use it to sign prime numbers, and distribute this program to other people. They can use the program to sign any prime number, but can't get the key out. But it's capable of much more than that: used with hashing, it can be used to implement any other cryptographic primitive, and more.
The only thing an obfuscated program can't do is prevent itself from being copied. But for that, there's something even more powerful on the horizon, although that depends on everyone having a quantum computer: quantum one-time signatures.
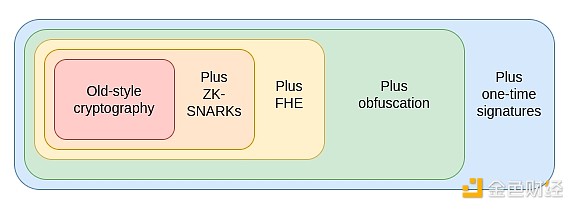
Using a combination of obfuscation and one-time signatures, we can build an almost perfect trustless third party. The only thing we can't do with cryptography alone, and what we still need blockchains to do, is guarantee censorship resistance. These techniques will not only allow us to make Ethereum itself more secure, but also build more powerful applications on top of Ethereum.
To understand how each of these primitives adds additional functionality, let's look at a key example: voting. Voting is a fascinating problem because it has many tricky security properties that need to be satisfied, including very strong verifiability and privacy. While voting protocols with strong security have existed for decades, let's make the problem harder by saying that we want a design that can handle arbitrary voting protocols: quadratic voting, pairwise bounded quadratic funding, cluster matching quadratic funding, and so on. That is, we want the "counting" step to be an arbitrary procedure.
First, suppose we put the votes publicly on the blockchain. This gives us public verifiability (anyone can verify that the final result is correct, including the counting rules and eligibility rules) and censorship resistance (people can't be stopped from voting). But we don't have privacy.
Then, we add ZK-SNARKs. Now, we have privacy: every vote is anonymous, while ensuring that only authorized voters can vote, and each voter can only vote once.
Now, we add the MACI mechanism. The votes are encrypted to a decryption key of a central server. The central server needs to run the counting process, including discarding duplicate votes, and publish a ZK-SNARK proving the answer. This preserves the previous guarantees (even if the server cheats!), but if the server is honest, it adds a coercion-resistant guarantee: users cannot prove how they voted, even if they wanted to. This is because, while users can prove the vote they cast, they cannot prove that they did not cast another vote that canceled that vote. This prevents bribery and other attacks.
We run the vote count inside FHE, and then do an N/2-of-N threshold decryption calculation to decrypt it. This makes the coercion-resistant guarantee N/2-of-N, rather than 1-of-1.
We obfuscate the vote count, and design the obfuscation so that it can only give output if it has permission, either through blockchain consensus proof, through a certain amount of proof-of-work, or both. This makes the coercion-resistant guarantee almost perfect: in the blockchain consensus case, you need 51% of the validators to collude to break it, and in the proof-of-work case, even if everyone colludes, it would be very expensive to re-run the vote count with a different subset of voters to try to extract the behavior of a single voter. We can even have the program make small random tweaks to the final result, making it harder to extract the behavior of individual voters.
We added one-time signatures, a primitive that relies on quantum computing, allowing a signature to be used only once to sign a message of a certain type. This makes the anti-coercion guarantee truly perfect.
Indistinguishability obfuscation also enables other powerful applications. For example:
DAOs, on-chain auctions, and other applications with arbitrary internal secret state.
True universal trusted setup: someone can create an obfuscated program that contains a key, and can run any program and provide the output, putting hash(key, program) as input into the program. Given such a program, anyone can put the program into itself, combining the program's existing key with their own key, and expanding the setup in the process. This can be used to generate 1-of-N trusted setups for any protocol.
ZK-SNARKs, whose verification is just the signature. Implementing this is simple: there is a trusted setup, and someone creates an obfuscated program that will sign a message with a key only if it is a valid ZK-SNARK.
Encrypted mempool. It becomes trivial to encrypt transactions so that they will only be decrypted if certain on-chain events occur in the future. This could even include successful execution of a VDF.
With one-time signatures, we can make blockchains immune to 51% finality reversal attacks, although censorship attacks are still possible. Primitives similar to one-time signatures could enable quantum money and solve the double-spending problem without a blockchain, although many more complex applications would still require a blockchain.
If these primitives can be made efficient enough, most of the world's applications could be decentralized. The main bottleneck is verifying the correctness of the implementation.
What research is there?
Indistinguishability Obfuscation Protocols in 2021: https://eprint.iacr.org/2021/1334.pdf
How Obfuscation Helps Ethereum: https://ethresear.ch/t/how-obfuscation-can-help-ethereum/7380
First Known One-Time Signature Construction: https://eprint.iacr.org/2020/107.pdf
Obfuscated attempted implementation (1): https://mediatum.ub.tum.de/doc/1246288/1246288.pdf
Obfuscated attempted implementation (2): https://github.com/SoraSuegami/iOMaker/tree/main
What's left to do, and what are the tradeoffs?
There's still a lot to do. Indistinguishability obfuscation is extremely immature, with candidate constructions running millions of times slower than applications (or more). Indistinguishability obfuscation is known for having a "theoretical" polynomial-time runtime, but in practice takes longer to run than the lifetime of the universe. Newer protocols make the runtimes less extreme, but the overhead is still too high for regular use: one implementer estimates a runtime of a year.
Quantum computers don't even exist: all the constructions you're likely to read about on the internet today are either prototypes that can't do any computations larger than 4 bits, or they're not real quantum computers, and while they may contain quantum parts, they can't run really meaningful computations like Shor's or Grover's algorithms. Recently, there have been signs that "real" quantum computers aren't that far away anymore. However, even if "real" quantum computers come out soon, the day when the average person has a quantum computer on their laptop or phone may be decades after a powerful institution gets one that can break elliptic curve cryptography.
For indistinguishability obfuscation, a key trade-off is security assumptions. There are more radical designs that use exotic assumptions. These generally have more realistic running times, but the exotic assumptions can sometimes be broken. Over time, we may eventually learn enough about lattices to make assumptions that can't be broken. However, this path is more dangerous. A more conservative approach is to stick with protocols whose security is provable as "standard" assumptions, but that may mean it takes us longer to get protocols that run fast enough.
How does it interact with the rest of the roadmap?
Extremely strong cryptography could be a game-changer. For example:
If we get ZK-SNARKs that are as easy to verify as signatures, we may not need any aggregation protocols; we can verify them directly on-chain.
One-time signatures could mean more secure proof-of-stake protocols.
Many complex privacy protocols could be replaced by “just” having a privacy-preserving EVM.
Encrypted memory pools become easier to implement.
First, the benefits will appear at the application layer, as Ethereum L1 inherently needs to be conservative in security assumptions. However, even using only the application layer could be a game changer, as the advent of ZK-SNARKs has.
 Weatherly
Weatherly

















