Tiêu đề gốc: Chữ ký bộ điều hợp và ứng dụng của nó đối với hoán đổi nguyên tử chuỗi chéo
Liên kết gốc: https:/ /blog.bitlayer.org/Adaptor_Signatures_and_Its_Application_to_Cross-Chain_Atomic_Swaps/
Tác giả: mutourend, lynndell
1. Giới thiệu
Với sự phát triển nhanh chóng của kế hoạch mở rộng Lớp 2 của Bitcoin, tần suất chuyển tài sản xuyên chuỗi giữa Bitcoin và mạng tương ứng Lớp 2 của nó đã tăng lên đáng kể . Xu hướng này được thúc đẩy bởi khả năng mở rộng cao hơn, phí giao dịch thấp hơn và thông lượng cao được cung cấp bởi các công nghệ Lớp 2 như Bitlayer. Những tiến bộ này tạo điều kiện thuận lợi cho các giao dịch hiệu quả và tiết kiệm hơn, từ đó thúc đẩy việc áp dụng và tích hợp Bitcoin rộng rãi hơn trên nhiều ứng dụng khác nhau. Do đó, khả năng tương tác giữa mạng Bitcoin và Lớp 2 đang trở thành một thành phần quan trọng của hệ sinh thái tiền điện tử, thúc đẩy sự đổi mới và cung cấp cho người dùng các công cụ tài chính mạnh mẽ và đa dạng hơn.
Như được hiển thị trong Bảng 1, có ba giải pháp điển hình cho các giao dịch chuỗi chéo giữa Bitcoin và Lớp 2, đó là giao dịch chuỗi chéo tập trung và chuỗi chéo BitVM cầu nối và hoán đổi nguyên tử chuỗi chéo. Ba công nghệ này khác nhau về giả định tin cậy, bảo mật, tiện lợi, giới hạn giao dịch, v.v. và có thể đáp ứng các nhu cầu ứng dụng khác nhau.
Bảng 1. So sánh các công nghệ giao dịch chuỗi chéo

Giao dịch chuỗi chéo tập trung: Người dùng là trên hết chuyển bit Nếu tiền tệ được trả cho một tổ chức tập trung (chẳng hạn như một bên tham gia dự án hoặc một sàn giao dịch), tổ chức tập trung sẽ trả giá trị tài sản tương đương cho địa chỉ do người dùng chỉ định trên mạng Lớp 2, do đó hoàn thành việc chuyển giao chéo chuyển giao tài sản chuỗi. Ưu điểm của công nghệ này là nhanh chóng và quá trình khớp lệnh tương đối dễ dàng vì tổ chức tập trung có thể nhanh chóng xác nhận và xử lý giao dịch. Tuy nhiên, tính bảo mật của phương pháp này hoàn toàn phụ thuộc vào độ tin cậy và uy tín của tổ chức tập trung. Nếu tổ chức tập trung gặp phải lỗi kỹ thuật, tấn công độc hại hoặc vỡ nợ, tiền của người dùng sẽ gặp rủi ro cao hơn. Ngoài ra, các giao dịch chuỗi chéo tập trung cũng có thể rò rỉ quyền riêng tư của người dùng và người dùng cần cân nhắc kỹ khi lựa chọn phương thức này. Do đó, mặc dù sự tiện lợi và hiệu quả của nó mang lại cho người dùng sự tiện lợi lớn nhưng tính bảo mật và tin cậy là những thách thức chính mà các giao dịch xuyên chuỗi tập trung phải đối mặt.
Cầu nối chuỗi chéo BitVM: Công nghệ này tương đối phức tạp. Đầu tiên, trong giai đoạn Peg-in, người dùng thanh toán Bitcoin đến một địa chỉ có nhiều chữ ký do Liên minh BitVM kiểm soát để khóa Bitcoin. Một số lượng mã thông báo tương ứng được tạo ra ở Lớp 2 và mã thông báo được sử dụng để triển khai các giao dịch và ứng dụng của Lớp 2. Khi người dùng hủy mã thông báo Lớp 2, nhà điều hành sẽ ứng trước khoản thanh toán. Sau đó, Nhà điều hành sẽ hoàn trả số Bitcoin tương ứng trong nhóm đa chữ ký do Liên minh BitVM kiểm soát. Để ngăn chặn người vận hành làm điều xấu, quy trình hoàn trả áp dụng cơ chế thách thức lạc quan, nghĩa là bất kỳ bên thứ ba nào cũng có thể thách thức các hành vi hoàn trả độc hại và ngăn chặn các hành vi xấu xa. Công nghệ này đưa ra cơ chế thử thách lạc quan nên công nghệ này tương đối phức tạp. Ngoài ra, cơ chế thử thách lạc quan bao gồm một số lượng lớn các giao dịch thử thách và phản hồi, với phí giao dịch cao hơn. Do đó, cầu nối chuỗi chéo BitVM chỉ phù hợp với các giao dịch rất lớn, tương tự như việc phát hành thêm U và do đó ít được sử dụng hơn.
Hoán đổi nguyên tử chuỗi chéo: Hoán đổi nguyên tử là một hợp đồng thực hiện các giao dịch tiền điện tử phi tập trung. Trong ngữ cảnh này, "nguyên tử" có nghĩa là sự thay đổi quyền sở hữu một tài sản thực sự có nghĩa là sự thay đổi quyền sở hữu một tài sản khác. Khái niệm này được TierNolan đề xuất lần đầu tiên trên diễn đàn Bitcointalk vào năm 2013. Trong bốn năm, sự hoán đổi nguyên tử vẫn nằm trong phạm vi lý thuyết. Cho đến năm 2017, Decred và Litecoin đã trở thành hệ thống blockchain đầu tiên hoàn thành thành công việc hoán đổi nguyên tử. Hoán đổi nguyên tử phải có sự tham gia của hai bên và không bên thứ ba nào có thể làm gián đoạn hoặc can thiệp vào quá trình hoán đổi. Điều này có nghĩa là công nghệ này phi tập trung, không bị kiểm duyệt, có khả năng bảo vệ quyền riêng tư tốt và có thể đạt được các giao dịch chuỗi chéo tần suất cao, do đó được sử dụng rộng rãi trong các sàn giao dịch phi tập trung. Hiện tại, trao đổi nguyên tử chuỗi chéo yêu cầu 4 giao dịch. Một số giải pháp cố gắng nén số lượng giao dịch xuống còn 2, nhưng điều này sẽ làm tăng yêu cầu trực tuyến theo thời gian thực cho cả hai bên trao đổi. Cuối cùng, công nghệ hoán đổi nguyên tử chuỗi chéo chủ yếu bao gồm khóa thời gian băm và chữ ký bộ điều hợp.
Hoán đổi nguyên tử chuỗi chéo dựa trên Hash Time Lock (HTLC): Dự án đầu tiên triển khai thành công hoán đổi nguyên tử chuỗi chéo là Decred, sử dụng "hash lock " " và "khóa thời gian" thực hiện trao đổi nguyên tử do TierNolan đề xuất với sự trợ giúp của các tập lệnh trên chuỗi (hoặc hợp đồng thông minh). HTLC cho phép hai người dùng thực hiện các giao dịch tiền điện tử có giới hạn thời gian, tức là người nhận phải gửi bằng chứng mật mã ("bí mật") cho hợp đồng trong một thời gian nhất định (được xác định theo số khối hoặc chiều cao khối), nếu không tiền sẽ được trả lại cho người dùng. người gửi Bởi. Nếu người nhận xác nhận thanh toán thì giao dịch thành công. Do đó, cả hai blockchain tham gia đều phải có chức năng “khóa băm” và “khóa thời gian”.
Mặc dù hoán đổi nguyên tử HTLC là một bước đột phá lớn trong lĩnh vực công nghệ sàn giao dịch phi tập trung, nhưng vẫn tồn tại những vấn đề sau. Các giao dịch hoán đổi nguyên tử này và dữ liệu liên quan đến chúng được thực hiện trên chuỗi, dẫn đến rò rỉ quyền riêng tư của người dùng. Nói cách khác, mỗi khi có một cuộc trao đổi, cùng một hàm băm sẽ xuất hiện trên cả hai chuỗi khối, cách nhau chỉ một vài khối. Điều này có nghĩa là người quan sát có thể so sánh mối tương quan giữa các loại tiền tệ tham gia trao đổi, tức là tìm cùng một giá trị băm trong các khối gần nhau (TimeStamp-wise). Khi theo dõi tiền tệ qua các chuỗi, rất dễ xác định nguồn gốc. Mặc dù phân tích này không tiết lộ bất kỳ dữ liệu nhận dạng liên quan nào nhưng các bên thứ ba có thể dễ dàng suy ra danh tính của các tác nhân liên quan.
Hoán đổi nguyên tử chuỗi chéo dựa trên chữ ký bộ chuyển đổi: Trao đổi thứ hai do BasicSwap cung cấp được gọi là hoán đổi nguyên tử "chữ ký bộ chuyển đổi", dựa trên bài báo A của nhà phát triển Monero Joël Gugger có tiêu đề "Hoán đổi nguyên tử chuỗi chéo Bitcoin–Monero}" được xuất bản vào năm 2020. Bài viết này có thể nói là sự triển khai của bài báo One-Time Verifiively Encrypted Signatures, A.K.A. Chữ ký bộ điều hợp là chữ ký bổ sung được kết hợp với chữ ký ban đầu để tiết lộ dữ liệu bí mật, cho phép cả hai bên tiết lộ đồng thời cả hai phần dữ liệu cho nhau và là thành phần chính của giao thức không có tập lệnh giúp các cặp hoán đổi nguyên tử của Monero có thể thực hiện được.
So với trao đổi nguyên tử HTLC, hoán đổi nguyên tử dựa trên chữ ký bộ điều hợp có 3 ưu điểm: Thứ nhất, sơ đồ trao đổi chữ ký bộ điều hợp thay thế trao đổi "băm bí mật" Phụ thuộc vào- tập lệnh chuỗi, bao gồm khóa thời gian và khóa băm. Nói cách khác, hàm băm bí mật và bí mật trong trao đổi HTLC không có sự tương ứng trực tiếp trong trao đổi chữ ký bộ điều hợp. Vì vậy, nó được gọi là “kịch bản không có chữ viết” trong cộng đồng nghiên cứu Bitcoin. Ngoài ra, do không có các tập lệnh như vậy tham gia nên không gian chiếm dụng trên chuỗi sẽ giảm đi, khiến cho việc hoán đổi nguyên tử dựa trên chữ ký của bộ điều hợp trở nên nhẹ hơn và rẻ hơn. Cuối cùng, HTLC yêu cầu mỗi chuỗi sử dụng cùng một giá trị băm và các giao dịch liên quan đến hoán đổi nguyên tử được ký bởi bộ điều hợp không thể được liên kết, để đạt được sự bảo vệ quyền riêng tư.
Bài viết này lần đầu tiên giới thiệu chữ ký bộ điều hợp Schnorr/ECDSA và nguyên tắc trao đổi nguyên tử chuỗi chéo. Sau đó, phân tích các vấn đề bảo mật số ngẫu nhiên tồn tại trong chữ ký bộ điều hợp cũng như các vấn đề về tính không đồng nhất của hệ thống và thuật toán trong các kịch bản chuỗi chéo và đưa ra giải pháp. Cuối cùng, chữ ký bộ điều hợp được mở rộng và áp dụng để thực hiện quyền giám sát tài sản kỹ thuật số không tương tác.
2. Chữ ký bộ điều hợp và trao đổi nguyên tử chuỗi chéo
2.1 Chữ ký bộ điều hợp Schnorr và nguyên tử trao đổi
 < /h2>
< /h2>
p>
2.2 Chữ ký bộ điều hợp ECDSA và Hoán đổi nguyên tử

2.2.1 Bằng chứng không có kiến thức zk{v | Ṽ = v ᐧ G, V = v ᐧ Y

3. Các vấn đề và giải pháp bảo mật
3.1 Bài toán và giải pháp về số ngẫu nhiên
3.1.1 Bài toán rò rỉ số ngẫu nhiên
Bộ chuyển đổi Schnorr/ECDSA Các chữ ký trước đã ký đều cam kết với một số ngẫu nhiên $r$ Ȓ = r ᐧ G. Ngoài ra, bằng chứng không có kiến thức cam kết số ngẫu nhiên $v$ thành $Ṽ=v ᐧ G,V=v ᐧ Y$. Nếu số ngẫu nhiên bị rò rỉ, khóa riêng sẽ bị rò rỉ.
Cụ thể, trong giao thức Schnorr, nếu số ngẫu nhiên $r$ bị rò rỉ, có thể xác định theo phương trình
$ŝ = r + c x.$
Tính khóa riêng $x$.
Tương tự, trong giao thức ECDSA, nếu số ngẫu nhiên $r$ bị rò rỉ, nó có thể được tính theo phương trình
$ŝ = r^{-1}(hash(m)+R_x x).$
Tính khóa riêng cho nhận được $x$.
Cuối cùng, trong giao thức chứng minh không có kiến thức, nếu số ngẫu nhiên $v$ bị rò rỉ, nó có thể được xác định theo phương trình
< p style="text-align: left;">$z := v + c r.$
Tính số ngẫu nhiên $r$, rồi tiếp tục tính toán dựa trên số ngẫu nhiên $r$ Trích xuất khóa riêng $x$. Vì vậy, những số ngẫu nhiên cần phải xóa ngay sau khi sử dụng.
3.1.2 Vấn đề sử dụng lại số ngẫu nhiên
Đối với bất kỳ hai giao dịch xuyên chuỗi nào, nếu Nếu giao thức chữ ký của bộ điều hợp sử dụng cùng một số ngẫu nhiên thì khóa riêng sẽ bị rò rỉ. Cụ thể, trong giao thức Schnorr, nếu sử dụng cùng một số ngẫu nhiên $r$ thì chỉ $r$ và $x$ là không xác định trong hệ phương trình sau
$ŝ_1 =r + c_1 x, $
$ ŝ_2 = r + c_2 x. : left;">Do đó, hệ phương trình có thể được giải để thu được khóa riêng $x$.
Tương tự, trong giao thức chữ ký bộ điều hợp ECDSA, nếu sử dụng cùng một số ngẫu nhiên $r$ thì chỉ có $r$ và $x$ trong hệ thống sau đây của phương trình chưa xác định
$ ŝ_1 = r^{-1}(hash(m_1)+R_x x),$
$ ŝ_2 = r^{-1}(hash(m_2)+R_x x).$
Do đó, hệ phương trình có thể được giải quyết, lấy khóa riêng $x$.
Cuối cùng, trong giao thức chứng minh không có kiến thức, nếu sử dụng cùng một số ngẫu nhiên $v$ thì chỉ có $v$ và $r$ trong hệ thống sau của các phương trình là Không xác định
$z_1 = v+c_1 r, $
$ z_2 = v+c_2 r. $
Do đó, hệ phương trình có thể được giải để thu được số ngẫu nhiên $r$ và hệ phương trình có thể là giải quyết thêm để lấy được khóa riêng $x$.
Tương tự, nếu những người dùng khác nhau sử dụng cùng một số ngẫu nhiên thì khóa riêng tư cũng sẽ bị rò rỉ. Nói cách khác, hai người dùng sử dụng cùng một số ngẫu nhiên có thể giải hệ phương trình và lấy được khóa riêng của nhau. Do đó, RFC 6979 nên được sử dụng để giải quyết vấn đề sử dụng lại số ngẫu nhiên.
3.1.3 Giải pháp: RFC 6979
RFC 6979 chỉ định một phương thức sử dụng DSA Phương thức việc tạo chữ ký số xác định bằng ECDSA giải quyết các vấn đề bảo mật liên quan đến việc tạo giá trị ngẫu nhiên k. Chữ ký DSA và ECDSA truyền thống dựa vào số k ngẫu nhiên được tạo ngẫu nhiên cho mỗi thao tác chữ ký. Nếu số ngẫu nhiên này được sử dụng lại hoặc tạo không đúng cách, tính bảo mật của khóa riêng có thể bị xâm phạm. RFC 6979 loại bỏ nhu cầu tạo số ngẫu nhiên bằng cách rút ra $k$ một cách xác định từ khóa riêng và thông báo được ký. Điều này đảm bảo rằng khi cùng một tin nhắn được ký bằng cùng một khóa riêng thì chữ ký luôn giống nhau, nâng cao khả năng tái tạo và dự đoán. Cụ thể, $k$ tất định được tạo ra bởi HMAC. Quá trình này bao gồm việc băm khóa riêng, tin nhắn và bộ đếm bằng hàm băm (chẳng hạn như SHA256),
$k = SHA256(sk, msg, counter) .$
Trong phương trình trên, để đơn giản trong biểu thức, giá trị băm chỉ được tính cho khóa riêng sk, thông báo tin nhắn và bộ đếm thực tế. quá trình trong RFC 6979 Có nhiều tính toán băm hơn. Phương trình này đảm bảo rằng k là duy nhất cho mỗi tin nhắn trong khi có thể tái tạo cho cùng một đầu vào và giảm nguy cơ lộ khóa riêng liên quan đến các trình tạo số ngẫu nhiên yếu hoặc bị xâm phạm. Do đó, RFC 6979 cung cấp một khuôn khổ mạnh mẽ cho chữ ký số xác định sử dụng DSA và ECDSA, giải quyết các vấn đề bảo mật quan trọng liên quan đến việc tạo số ngẫu nhiên và nâng cao độ tin cậy cũng như khả năng dự đoán của chữ ký số. Điều này làm cho nó trở thành một tiêu chuẩn có giá trị cho các ứng dụng yêu cầu tính bảo mật cao và tuân thủ các yêu cầu vận hành nghiêm ngặt. Chữ ký Schnorr/ECDSA có lỗi số ngẫu nhiên và RFC 6979 cần được sử dụng để ngăn chặn chúng. Do đó, chữ ký bộ điều hợp dựa trên Schnorr/ECDSA cũng có những vấn đề này và đặc tả RFC 6979 cũng cần được sử dụng để giải quyết những vấn đề này.
3.2 Các vấn đề và giải pháp trong kịch bản chuỗi chéo
3.2.1 UTXO và hệ thống mô hình tài khoản Các vấn đề và giải pháp không đồng nhất
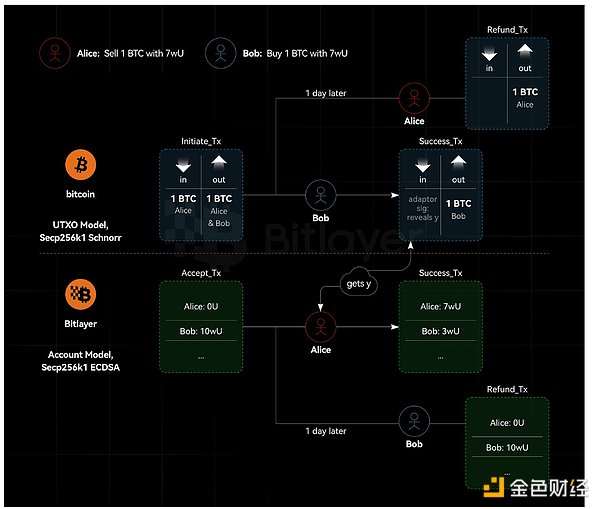
Như được hiển thị trong Hình 1, Bitcoin sử dụng mô hình UTXO để triển khai chữ ký ECDSA gốc dựa trên đường cong Secp256k1. Bitlayer tương thích EVM với chuỗi Bitcoin L2, sử dụng đường cong Secp256k1 và hỗ trợ chữ ký ECDSA gốc. Adaptor Signature triển khai logic cần thiết cho các giao dịch hoán đổi BTC, trong khi đối tác hoán đổi Bitlayer được hỗ trợ bởi sức mạnh của các hợp đồng thông minh Ethereum.
Hoán đổi nguyên tử chuỗi chéo dựa trên chữ ký bộ điều hợp hoặc ít nhất là sơ đồ chữ ký bộ điều hợp bán không có tập lệnh được thiết kế để hoạt động với đường cong ECDSA, không tương thích với Ethereum. Lý do là Ethereum là mô hình tài khoản chứ không phải mô hình UTXO. Cụ thể, các giao dịch hoán đổi nguyên tử dựa trên chữ ký của bộ điều hợp yêu cầu các giao dịch hoàn tiền phải được ký trước. Tuy nhiên, trong hệ thống Ethereum, các giao dịch không thể được ký trước nếu không biết nonce. Do đó, một bên có thể gửi giao dịch giữa lúc hoàn thành việc ký trước và thực hiện giao dịch - điều này sẽ làm mất hiệu lực giao dịch được ký trước (vì số nonce đã được sử dụng và không thể sử dụng lại).
Ngoài ra, từ góc độ quyền riêng tư, điều này có nghĩa là tính ẩn danh của trao đổi Bitlayer tốt hơn HTLC (cả hai bên tham gia trao đổi đều có thể tìm thấy hợp đồng). Tuy nhiên, do một bên bắt buộc phải có hợp đồng công khai nên tính ẩn danh của trao đổi Bitlayer thấp hơn chữ ký của bộ điều hợp. Không có hợp đồng ở một bên, giao dịch hoán đổi trông giống như bất kỳ giao dịch nào khác. Tuy nhiên, về phía hợp đồng EVM, giao dịch này rõ ràng là để hoán đổi tài sản. Mặc dù một bên có hợp đồng công khai nhưng không thể theo dõi nó từ chuỗi khác, thậm chí sử dụng các công cụ phân tích chuỗi phức tạp.
 p>
p>
Hình 1. UTXO và mô hình tài khoản hệ thống không đồng nhất trao đổi nguyên tử chuỗi chéo
Bitlayer hiện tại hỗ trợ chữ ký ECDSA gốc và xác minh chữ ký Schnorr cũng có thể được thực hiện thông qua hợp đồng thông minh. Nếu bạn sử dụng các giao dịch Bitlayer gốc, bạn không thể ký trước các giao dịch hoàn tiền trong các giao dịch hoán đổi nguyên tử; bạn cần sử dụng các giao dịch hợp đồng thông minh Bitlayer để đạt được các giao dịch hoán đổi nguyên tử. Tuy nhiên, quá trình này sẽ hy sinh quyền riêng tư, tức là các giao dịch tham gia hoán đổi nguyên tử trong hệ thống Bitlayer có thể theo dõi được, còn các giao dịch trong hệ thống BTC thì không thể theo dõi được. Các ứng dụng Dapp như Tornado Cash có thể được thiết kế ở phía Bitlayer để cung cấp dịch vụ bảo mật cho các giao dịch ở phía Bitlayer trong các giao dịch hoán đổi nguyên tử BTC và Bitlayer.
3.2.2 Cùng một đường cong, thuật toán khác nhau, bảo mật chữ ký bộ điều hợp
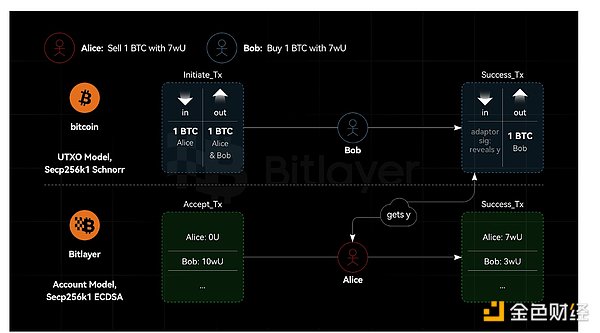
Như trong Hình 2 Như trong hình, giả định rằng cả Bitcoin và Bitlayer đều sử dụng đường cong Secp256k1, nhưng Bitcoin sử dụng chữ ký Schnorr và Bitlayer sử dụng ECDSA. Trong trường hợp này, chữ ký bộ điều hợp dựa trên Schnorr và ECDSA được chứng minh là an toàn. Giả sử rằng các oracle chữ ký ECDSA và Schnorr đã cho, trình mô phỏng S có thể được xây dựng để phá vỡ ECDSA, sau đó chỉ được cung cấp oracle chữ ký ECDSA, trình mô phỏng S có thể được xây dựng để phá vỡ ECDSA. Tuy nhiên, ECDSA an toàn. Theo cách tương tự, giả sử rằng với các oracle chữ ký ECDSA và Schnorr, trình mô phỏng S có thể được xây dựng để phá vỡ chữ ký Schnorr, sau đó chỉ cho oracle chữ ký ECDSA, thì trình mô phỏng S có thể được xây dựng để phá vỡ chữ ký Schnorr. Tuy nhiên, chữ ký Schnorr được bảo mật. Do đó, trong kịch bản chuỗi chéo, nếu chữ ký bộ điều hợp sử dụng cùng một đường cong nhưng thuật toán chữ ký khác nhau thì điều đó là an toàn. Nói cách khác, việc ký bộ chuyển đổi cho phép một đầu sử dụng ECDSA và đầu kia sử dụng chữ ký Schnorr.
 p>
p>
Hình 2. Cùng một đường cong, thuật toán khác nhau, chữ ký bộ điều hợp
3.2.3 Đường cong khác nhau , adapter Chữ ký không an toàn
Giả sử rằng Bitcoin sử dụng đường cong Secp256k1 và chữ ký ECDSA, trong khi Bitlayer sử dụng đường cong ed25519 và chữ ký Schnorr. Trong trường hợp này, chữ ký bộ điều hợp không thể được sử dụng. Do các đường cong khác nhau nên thứ tự của nhóm đường cong elip cũng khác nhau, tức là các hệ số mô đun cũng khác nhau. Khi Bob điều chỉnh $y$ cho phù hợp với chữ ký ECDSA trong hệ thống Bitcoin, anh ấy tính toán $s:= ŝ+y$. Lúc này, không gian giá trị của $y$ là không gian vô hướng của nhóm đường cong elip Secp256k1. Sau đó, Alice cần sử dụng $y$ để thực hiện chữ ký Schnorr trên nhóm đường cong elip ed25519. Tuy nhiên, hệ số của đường cong ed25519 là 8 và hệ số mô-đun không bằng hệ số mô-đun của nhóm đường cong elip Secp256k1. Do đó, sẽ không an toàn khi sử dụng $y$ cho chữ ký Schnorr trên đường cong ed25519.
4. Đơn đăng ký lưu ký tài sản kỹ thuật số
Quyền lưu ký tài sản kỹ thuật số có ba người tham gia, cụ thể là: Người mua Alice, người bán Bob và bên ký quỹ. Việc sử dụng chữ ký bộ điều hợp cho phép lưu giữ tài sản kỹ thuật số ở ngưỡng không tương tác và khởi tạo một tập hợp con các chiến lược chi tiêu ngưỡng mà không cần tương tác. Tập hợp con này bao gồm hai loại người tham gia: những người tham gia khởi tạo và những người tham gia không tham gia khởi tạo. Người giám sát không thể ký các giao dịch tùy tiện và chỉ gửi bí mật cho một trong các bên hỗ trợ.
Một mặt, người giám sát chỉ có thể chọn trong số một số giao dịch thanh toán cố định và không thể ký giao dịch mới với một trong các bên khác. Do đó, cơ chế phát hành bí mật này làm cho việc lưu trữ ngưỡng không tương tác kém linh hoạt hơn so với chữ ký Schnorr ngưỡng. Mặt khác, chính sách chi tiêu 2 trên 3 có thể được thiết lập bằng cách sử dụng chữ ký Schnorr ngưỡng. Tuy nhiên, ngưỡng giao thức chữ ký Schnorr yêu cầu ba bên chạy giao thức tạo khóa phi tập trung. Do đó, các giao thức ký quỹ tài sản dựa trên chữ ký của bộ điều hợp có ưu điểm là không tương tác.
4.1 Lưu trữ nội dung không tương tác dựa trên chữ ký bộ chuyển đổi

Hình 3. Tính phi tuyến tính dựa trên chữ ký bộ điều hợp Ký quỹ tài sản tương tác
Như được hiển thị trong Hình 3, Alice và Bob muốn tạo đầu ra giao dịch 2 trên 3 bằng chiến lược lén lút có chứa ký quỹ quảng trường. Tùy thuộc vào điều kiện $c$, Alice hoặc Bob có thể chi tiêu đầu ra giao dịch. Nếu có tranh chấp giữa Alice và Bob, người giám sát (khóa chung $E$, khóa riêng $e$) sẽ quyết định xem Alice hay Bob có được tài sản hay không.
Tạo một giao dịch cấp vốn chưa ký để gửi BTC cho ai đó giữa Alice và Bob 2-of- 2 đầu ra MuSig.
Alice chọn một giá trị ngẫu nhiên $t_A$ và gán chữ ký trước Schnorr$ của bộ điều hợp giao dịch cho $t_A ᐧ G$ (\hat{R__A,\hat{s__A)$ được gửi cho Bob. Giao dịch này nhằm gửi đầu ra tài trợ cho Bob. Alice cũng gửi một bản mã cho Bob, văn bản này chứa \textbf{mã hóa có thể kiểm chứng}$ của bí mật $t_A$ và điều chỉnh khóa công khai ký quỹ $E$ thành $E_c = E + hash(E, c)G$ C = Enc (E_c, t_A)$. Trong quá trình này, sau khi Bob nhận được chữ ký trước của Alice, anh ta sẽ thêm chữ ký của chính mình, chữ ký này không thỏa mãn MuSig 2 trên 2 và do đó không thể sử dụng số tiền tài trợ đầu ra. Số tiền tài trợ chỉ có thể được sử dụng nếu Bob biết $t_A$ (được cung cấp bởi ký quỹ) hoặc nếu Alice ký thêm chữ ký hoàn chỉnh và gửi nó cho Bob.
Tương ứng, Bob lặp lại bước (2) dựa trên bí mật bộ điều hợp $t_B$ của anh ấy. Giao dịch được Bob ký vào lúc này là để gửi kết quả tài trợ cho Alice.
Cả Alice và Bob đều xác minh tính hợp lệ của bản mã nhận được và xác nhận rằng bản mã đó là mã hóa của bí mật $E_c$, do đó Ký và phát sóng giao dịch tài trợ. Mã hóa có thể xác minh giúp loại bỏ nhu cầu người giám sát tham gia vào giai đoạn thiết lập và không yêu cầu hợp đồng công khai $c$.
Khi có tranh chấp, Alice và Bob có thể gửi bản mã và điều kiện c cho người giám sát và người giám sát có thể Tình huống thực tế được xác định và khóa riêng $e+hash(E, c)$ đã điều chỉnh được sử dụng để giải mã và gửi $t_A/t_B$ cho Bob/Alice.
Nếu không có tranh chấp, Alice và Bob có thể sử dụng sản lượng 2/2 MuSig theo ý muốn. Nếu có tranh chấp, một trong hai bên có thể liên hệ với bên ký quỹ và yêu cầu bí mật bộ điều hợp $t_A$ hoặc $t_B$. Do đó, một trong các bên, với sự trợ giúp của bên ký quỹ, có thể hoàn thành chữ ký bộ điều hợp và phát sóng giao dịch thanh toán.
4.2 Mã hóa có thể kiểm chứng
Lược đồ mã hóa có thể kiểm chứng cổ điển dựa trên logarit rời rạc (Mã hóa có thể xác minh thực tế và Không thể sử dụng giải mã logarit rời rạc) với bộ điều hợp Secp256k1 vì nó chỉ hỗ trợ xác minh các nhóm có cấu trúc đặc biệt.
Hiện tại, có hai cách hứa hẹn để thực hiện mã hóa có thể kiểm chứng dựa trên logarit rời rạc Secp256k1, đó là Purify và Juggle.
Purify ban đầu được đề xuất để tạo giao thức MuSig với nonce xác định (DN), yêu cầu mỗi người ký phải sử dụng kiến thức bằng 0 để chứng minh rằng nonce của nó là sai Kết quả của hàm ngẫu nhiên (PRF) được áp dụng chính xác cho khóa chung và thông báo. Purify PRF có thể được triển khai một cách hiệu quả trong mạch số học của giao thức không có kiến thức Bulletproofs để tạo các sơ đồ mã hóa có thể kiểm chứng trên logarit rời rạc trên Secp256k1. Nói cách khác, hãy sử dụng zkSnark để triển khai mã hóa có thể kiểm chứng.
Mã hóa tung hứng bao gồm bốn bước: (1) Chia logarit rời rạc $x$ thành nhiều đoạn $x_k$ có độ dài $l$, Tạo $x = \ sum _k 2^{(k-1)l} x_k$; (2) Sử dụng khóa chung $Y$ để thực hiện mã hóa ElGamal trên đoạn $x_k ᐧ ᐧ
Trong quá trình giải mã, $\{D_k, E_k\}$ được giải mã để lấy từng $x_k ᐧ G$, sau đó $x_k được tìm kiếm toàn diện $ (phạm vi giá trị là $[0, 2^l)$).
Purify cần thực hiện PRF trong Bulletproofs, việc này tương đối phức tạp, trong khi Juggles đơn giản hơn về mặt lý thuyết. Ngoài ra, sự khác biệt giữa cả hai về kích thước bằng chứng, thời gian chứng minh và thời gian xác minh là rất nhỏ.
5. Tóm tắt
Bài viết này thảo luận về chữ ký bộ điều hợp Schnorr/ECDSA và chuỗi chéo trao đổi nguyên tử Các nguyên tắc được mô tả chi tiết. Một phân tích chuyên sâu về các vấn đề rò rỉ và trùng lặp số ngẫu nhiên trong chữ ký bộ điều hợp đã được tiến hành và việc sử dụng RFC 6979 đã được đề xuất để giải quyết các vấn đề này. Ngoài ra, nó phân tích chi tiết rằng trong các kịch bản ứng dụng chuỗi chéo, không chỉ cần xem xét sự khác biệt giữa mô hình UTXO và mô hình tài khoản của chuỗi khối mà còn xem liệu chữ ký bộ điều hợp có hỗ trợ các thuật toán khác nhau, các đường cong khác nhau và các vấn đề khác hay không. Cuối cùng, chữ ký bộ điều hợp được mở rộng và áp dụng để thực hiện quyền giám sát tài sản kỹ thuật số không tương tác và các nguyên tắc mã hóa cơ bản có liên quan - mã hóa có thể kiểm chứng - được giới thiệu ngắn gọn.
Tài liệu tham khảo
Gugger J. Hoán đổi nguyên tử chuỗi chéo Bitcoin-monero[J]. Cryptology ePrint Archive, 2020.
Fournier L. One - thời gian chữ ký được mã hóa có thể xác minh hay còn gọi là chữ ký bộ điều hợp[J].
https://crypto-in-action. .io/ecdsa-blockchain-dangers/190816-secp256k1-ecdsa-dangers.pdf
Pornin T. Cách sử dụng kỹ thuật số mang tính quyết định thuật toán chữ ký (DSA) và thuật toán chữ ký số đường cong elip (ECDSA)[R].
Komlo C, Goldberg I . FROST: chữ ký ngưỡng Schnorr được tối ưu hóa theo vòng linh hoạt[C]//Các lĩnh vực được chọn trong Mật mã học: Hội nghị quốc tế lần thứ 27, Halifax, NS, Canada (Sự kiện ảo), ngày 21-23 tháng 10 năm 2020, Các bài báo được chọn đã sửa đổi 27. Nhà xuất bản quốc tế Springer, 2021 : 34-65.
https://github.com/BlockstreamResearch/scriptless-scripts/blob/master/md/ NITE .md
https://particl.news/the-dex-revolution-basicswap-and-private-ethereum-swaps /
Camenisch J, Shoup V. Mã hóa và giải mã có thể kiểm chứng thực tế của logarit rời rạc[C]//Hội nghị mật mã quốc tế thường niên Berlin ,. Heidelberg: Springer Berlin Heidelberg, 2003: 126-144.
Nick J, Ruffing T, Seurin Y, et al. DN: Schnorr đa chữ ký với các số không xác định có thể xác minh được[C]//Kỷ yếu của Hội nghị ACM SIGSAC 2020 về Bảo mật Máy tính và Truyền thông 2020: 1717-1731.
Slomovits O, Leiba O. Juggleswap: hoán đổi chuỗi chéo nguyên tử không có tập lệnh[J]. arXiv bản in trước arXiv:2007.14423, 2020.
 Brian
Brian


 < /h2>
< /h2>

 p>
p> p>
p>



