المؤلف: Quantodian المصدر: متوسط ​​الترجمة: Shan Oppa, Golden Finance

مقدمة

تم اقتراح قانون الطاقة المستند إلى الوقت في البيتكوين لأول مرة من قبل جيوفاني سانتوستاسي في وقت مبكر من عام 2014، وفي عام 2019 أعيد- تم التعبير عنها من قبلنا (إما كممر أو كنموذج ثلاثي المعلمات)، وتم وصف العلاقة بين سعر البيتكوين والوقت. على وجه التحديد، يصف النموذج العلاقة الخطية بين لوغاريتم عدد الأيام منذ كتلة نشأة البيتكوين ولوغاريتم سعر البيتكوين بالدولار الأمريكي.

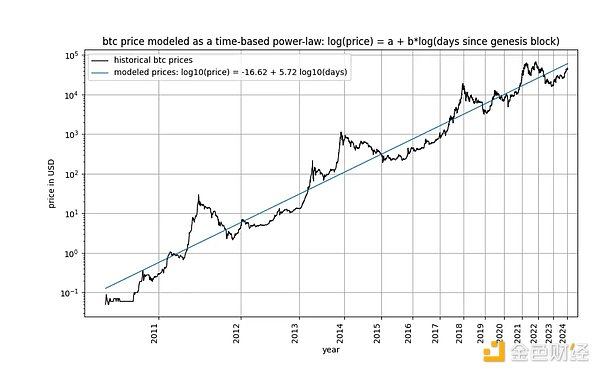p>

لقد اجتذب النموذج العديد من النقاد، بما في ذلك مارسيل برجر، وتيم ستولت، ونيك إمبلو، الذين كتب كل منهم "تفنيدات" للنموذج. في هذه المقالة، نهدف إلى تحليل إحدى الحجج الرئيسية في هذه الانتقادات الثلاثة: الافتقار المزعوم للتكامل المشترك بين الوقت والسعر، والذي يرفض النموذج باعتباره "غير صالح" ويشير فقط إلى علاقة زائفة.

هل هذا هو الحال بالفعل؟

في هذه المقالة سوف ندرس هذه المشكلة بدقة. وهذا يقودنا إلى استنتاج مفاده أن التكامل المشترك، بالمعنى الدقيق للكلمة، لا يمكن أن يوجد في النماذج المعتمدة على الوقت، بما في ذلك نماذجنا الخاصة. ومع ذلك، لا يمكن إنكار أن إحدى الخصائص الإحصائية اللازمة للتكامل المشترك موجودة في نماذج قانون القوة المستندة إلى الزمن. لذلك، نستنتج أن قوانين القوة المستندة إلى الزمن متكاملة بشكل فضفاض، وأن منتقدينا مخطئون، وأن النموذج صالح تمامًا. لقد أظهرنا أن هذا الاستنتاج ينطبق بشكل متساوٍ على نموذج المخزون إلى التدفق (S2F) والنمو الأسي الملحوظ في أسعار مؤشرات سوق الأسهم على المدى الطويل.

مقدمة للمفاهيم

التكامل المشترك

هل أنت ضائع بالفعل؟ ربما كلمة "التكامل المشترك" غير مألوفة بالنسبة لك؟ لا تقلق: يدعي جوديا بيرل، الخبير في الاستدلال السببي والعلاقات غير الزائفة ومؤلف كتاب لماذا، أنه لا يعرف شيئًا عن هذا الموضوع. وسنسعى إلى توضيح المصطلحات ذات الصلة بالمسألة المطروحة بشكل كامل.

p>

من المثير للاهتمام والرائع هو الجدل المحتدم حول التكامل المشترك حول X داخل مساحة #bitcoin، والذي يتميز بالسطحية الواضحة للموضوع. العديد من أتباع قوانين تدفق المخزون والطاقة في حيرة من أمرهم. يمكن للقراء المهتمين رؤية ذلك بأنفسهم عن طريق إدخال عبارة البحث "ما هو التكامل المشترك" في X. في حين يبدو أن بعض المساهمين قد أتقنوا فهمهم وصقلوه بمرور الوقت، إلا أن آخرين يظلون مشوشين، أو يغيرون جانبهم، أو يصبحون مشوشين. ولم نناقش هذا الموضوع حتى الآن.

أولاً بعض الخلفية

تتضمن العمليات العشوائية متغيرات عشوائية. لم يتم تحديد قيمة المتغير العشوائي مسبقًا. في المقابل، يمكن التنبؤ بالعملية الحتمية بدقة مسبقًا، فكل جانب منها معروف مسبقًا. أشياء مثل أسعار سوق الأوراق المالية تكون عشوائية لأننا لا نستطيع التنبؤ بسعر الأصل في وقت مبكر. ولذلك، فإننا نتعامل مع السلاسل الزمنية مثل أسعار الأسهم أو البيتكوين كملاحظات لمتغيرات عشوائية.

بدلاً من ذلك، يتبع مرور الوقت نمطًا حتميًا. كل ثانية، كل لحظة تمر - دون أي شك. ولذلك، فإن المدة التي تنقضي بعد وقوع الحدث هي متغير حتمي.

ثباتية الإشارة

قبل دراسة التكامل المشترك، دعونا أولاً نلقي نظرة على التكامل المشترك المفهوم الأساسي للتكامل: الثبات:

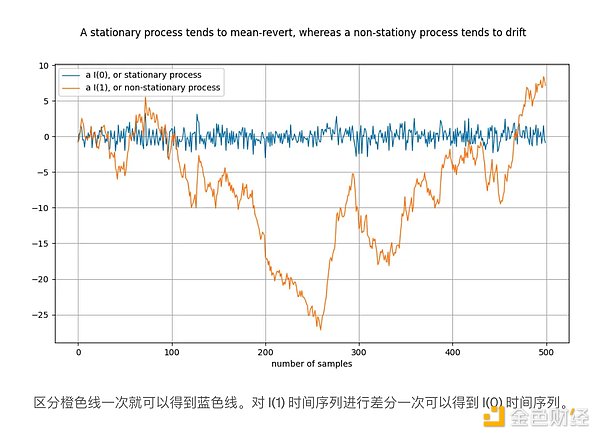
العملية الثابتة هي عملية عشوائية، بشكل عام، لها نفس الخصائص مع مرور الوقت. ومن أمثلة هذه الخصائص المتوسط ​​والتباين، وهما محددان ومستقران لعملية ثابتة. مرادف للسلسلة الزمنية الثابتة هو I (0). يجب ألا "تنجرف" السلاسل الزمنية من العمليات الثابتة ويجب أن تميل إلى العودة إلى المتوسط، وهو الصفر عادةً.

مثال على عملية غير ثابتة هو السير العشوائي، الذي يصف الحركة البراونية أو انتشار الجسيمات في الفيزياء: كل قيمة جديدة في السير العشوائي تعتمد على إضافة رقم عشوائي للقيمة السابقة. تختلف خصائص العملية غير الثابتة، مثل المتوسط ​​والتباين، بمرور الوقت أو لم يتم تحديدها. العمليات غير الثابتة هي I(1) أو أعلى، ولكن عادةً ما تكون I(1). "تنجرف" السلاسل الزمنية الناشئة عن العمليات غير الثابتة بمرور الوقت، أي تميل إلى الابتعاد عن أي قيمة ثابتة.

يشير الترميز I(1) إلى التكرار الذي يجب أن "تختلف" عنده السلسلة الزمنية قبل أن تصل إلى حالة الثبات. الفرق هو الفرق بين قيمة في سلسلة زمنية وقيمتها السابقة. وهذا يعادل تقريبا أخذ المشتق. السلسلة الزمنية الثابتة ثابتة بالفعل - يجب أن تختلف بمقدار 0 مرة لتكون ثابتة، لذا فهي I(0). يجب التمييز بين السلسلة الزمنية I(1) مرة واحدة قبل أن تصبح ثابتة.

تم إنشاء الشكل أعلاه عن طريق إجراء فرق على السلسلة الزمنية البرتقالية للحصول على السلسلة الزمنية الزرقاء. وبشكل مكافئ، يتم الحصول على السلسلة الزمنية البرتقالية من خلال دمج السلسلة الزمنية الزرقاء.

تشير عملية جذر الوحدة هنا إلى نموذج الانحدار الذاتي (بشكل أكثر دقة من النوع AR(1)) حيث تُقدر المعلمة rho بأنها تساوي 1 . على الرغم من أننا نستخدم rho وroot بالتبادل، إلا أن rho يشير إلى العمليات التي غالبًا ما تكون غير معروفة وتحتاج إلى تقدير. النتيجة المقدرة هي القيمة "الجذر".

تمثل قيمة rho مدى تذكر العملية لقيمها السابقة. وتشير قيمة u إلى مصطلح الخطأ، الذي يُفترض أنه ضوضاء بيضاء.

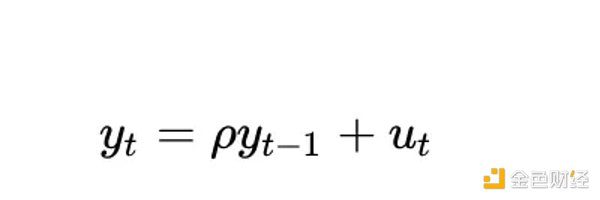p>

عملية جذر الوحدة هي عملية عشوائية وغير ثابتة. العمليات ذات قيم "الجذر" أو rho أقل من 1 لا تميل إلى الانحراف وبالتالي فهي ثابتة. على المدى الطويل، حتى القيم القريبة من (ولكن أقل) من 1 سوف تميل نحو متوسط ​​الارتداد (بدلاً من الانحراف). لذلك، تعتبر عملية جذر الوحدة مميزة لأنها تتصرف بشكل مختلف بشكل أساسي عن العمليات التي تكون جذورها قريبة جدًا من 1. يوضح الشكل أدناه 4 عينات من البيانات التي تم إنشاؤها بواسطة 4 عمليات انحدار ذاتي معروفة، ولكل منها قيمة rho مختلفة.

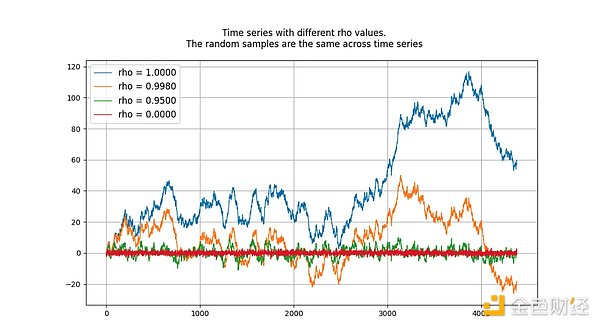p>

التكامل المشترك لإشارتين

متغيرين عشوائيين (في حالتنا الزمن الحضور أو الغياب التكامل المشترك بين المتتابعات). لكي يكون الزوجان متكاملين، يجب أن يكونا متكاملين بنفس الترتيب وأن يكونا غير ثابتين. علاوة على ذلك (وهذا هو الجزء الأساسي)، يجب أن يكون هناك مزيج خطي ثابت من السلسلتين الزمنيتين.

مثال على عدم وجود إشارة تكامل مشترك

إذا كانت السلسلتان الزمنيتان غير ثابتتين، إذن غالبًا ما تكون التركيبات الخطية (وفي هذه الحالة نختار ببساطة الفرق بين سلسلتين زمنيتين) غير ثابتة أيضًا:

مثال على الإشارة المتكاملة

h2>< p style="text-align: left;">إذا انجرفت سلسلتان زمنيتان غير ثابتتين "بنفس الطريقة" على المدى الطويل، فيمكن أن تكون المجموعة الخطية (هنا نختار r2–0.5*r1) ثابتة:< /p>

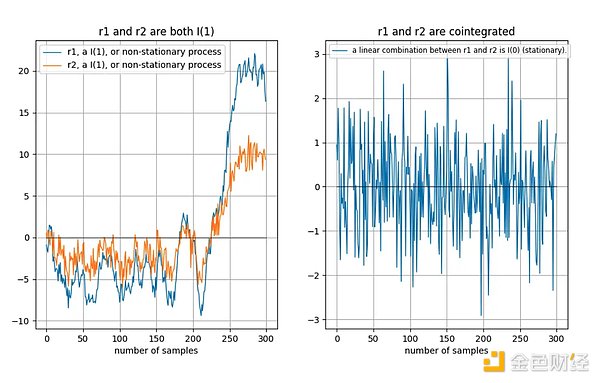
يقدم تو وآخرون [1] وصفًا مرئيًا جيدًا للتكامل المشترك:

"إن وجود علاقة تكامل مشترك بين السلاسل الزمنية يعني أن لها انجراف عشوائي مشترك على المدى الطويل."

لماذا يكون من المفيد أن يكون لسلسلتين زمنيتين غير ثابتتين مجموعة خطية ثابتة؟ لنفترض أن لدينا سلسلتين زمنيتين x وy، ونحاول صياغة y بناءً على x: y = a + b*x. يتم إعطاء خطأ النموذج الخاص بنا من خلال المجموعة الخطية من x و y: خطأ النموذج = y — a — b*x . ونأمل أن يكون خطأ هذا النموذج مستقرا، أي ألا ينحرف على المدى الطويل. إذا تضاءل خطأ النموذج على المدى الطويل، فهذا يعني أن نموذجنا سيئ، وغير قادر على تقديم تنبؤات دقيقة.

الشيطان يكمن في التفاصيل

يمكن العثور على تعريف أكثر رسمية في Engle و "التكامل المشترك" وتصحيح الخطأ لجرانجر: التمثيل والتقدير والاختبار" [2] (جرانجر هو مخترع مفهوم التكامل المشترك وحصل على جائزة نوبل في الاقتصاد عام 2003)، والذي يحدد المفاهيم والاختبارات الأساسية للكشف عن التكامل المشترك. مفتاح هذه الورقة هو الافتراض بأن السلسلة الزمنية عشوائية ولا تحتوي على عنصر حتمي (سنناقش هذا لاحقًا).

p>

مطبق على الوقت وسعر البيتكوين

في حالة قانون القوة المستند إلى الوقت ، هناك متغيران:

1. log_time: لوغاريتم عدد الأيام منذ كتلة التكوين

2. log_price : لوغاريتم السعر

وفقًا لتعريفات إنجل وجرانجر، يجب أن يكون كلا المتغيرين متغيرين عشوائيين، وليس لهما مكونات حتمية، ويجب أن يكونا غير ثابتين. علاوة على ذلك، يجب أن نكون قادرين على إيجاد مجموعة خطية ثابتة من متغيرين. وبخلاف ذلك لا يوجد تكامل مشترك بين المتغيرين.

قبل الخوض في التفاصيل، لنعرض أولاً بعض الرسوم البيانية لبيانات النموذج نفسها، دون أي فكرة عن مفاهيم الثبات أو التكامل المشترك. لاحظ أن قانون القوة المعتمد على الزمن ينتج توافقًا يبدو جيدًا جدًا من الناحية البصرية. لا يشير المتجه المتبقي على الفور إلى الانجراف.

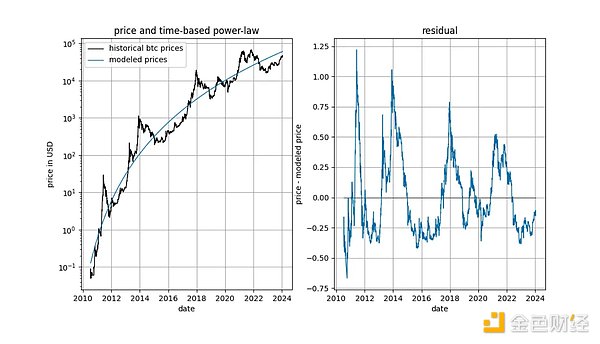p>

علاوة على ذلك، يُظهر النموذج أداءً ممتازًا خارج العينة (انظر أدناه). لا يتوافق الأداء الممتاز خارج العينة مع الادعاء بأن النموذج زائف - فالنموذج المبني على الارتباطات الزائفة يجب أن يكون: زائفًا، مما يعني أنه لا يمكنه التنبؤ بدقة. يمكن اختبار الأداء خارج العينة عن طريق ملاءمة النموذج لكمية محدودة من البيانات (حتى تاريخ معين) والتنبؤ بالفترة الزمنية التي لا يتناسب فيها النموذج (على غرار التحقق من الصحة المتبادل). خلال فترة خارج العينة، تستمر الأسعار المرصودة في عبور الأسعار النموذجية بشكل متكرر، ولا تتحرك أكبر الانحرافات في الأسعار المرصودة بشكل منهجي بعيدًا عن الأسعار النموذجية.

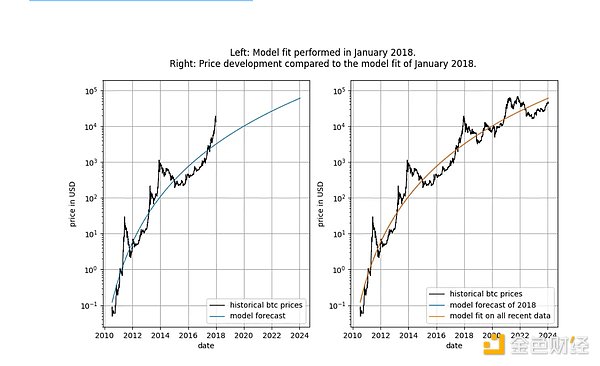p>

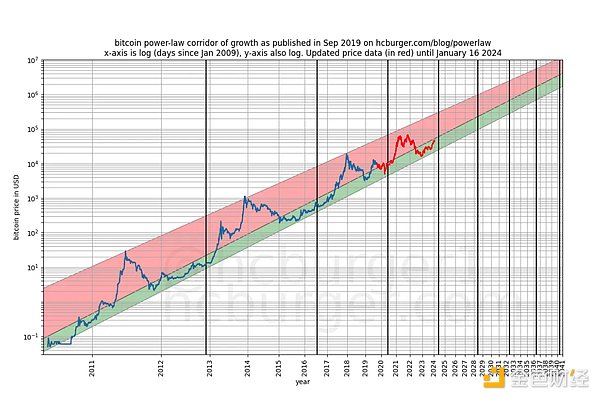
يمكننا أن ننظر بدقة أكبر إلى أداء النموذج بعد إصداره (سبتمبر 2019) لأننا لا نستطيع الغش بأي شكل من الأشكال بعد إصدار النموذج - لا يمكننا تغييره بعد واقعة النموذج.

p>

أي اتهام بأن النموذج يعتمد فقط على ارتباطات زائفة يجب أن يؤخذ بحذر فيما يتعلق بالقوة التنبؤية للنموذج.

التكامل المشترك خطوة بخطوة

من أجل تمكين التكامل المشترك بين log_time وlog_price يجب أن يكون كل متغير متغيرًا عشوائيًا متكاملاً من نفس الترتيب، ويجب أن يكون على الأقل من الرتبة 1.

log_price متغير

هل log_price سلسلة زمنية ثابتة؟ يخلص نيك إلى أنه باستخدام اختبار ADF ذو النمط غير المحدد (اختبار عدم الثبات) واختبار KPSS (اختبار الثبات)، فإن السجل (السعر) هو بلا شك غير ثابت وبالتالي I(1) أو أعلى. استنتج مارسيل برجر بالفحص البصري أنني (1). قدم تيم ستولت ملاحظة أكثر إثارة للاهتمام: فقد أجرى اختبارات ADF على فترات زمنية مختلفة (لم يتم تحديد نمط محدد) وأشار إلى أن الوضع ليس واضحًا: "لذلك، لا يمكننا أن نرفض بشدة عدم الاستقرار ونستنتج أن هناك سعرًا لوغاريتميًا علامات عدم الاستقرار."

دعونا نجري التحليل الخاص بنا. كما هو الحال مع Tim Stolte، سنطبق اختبار ADF في نوافذ زمنية مختلفة: نبدأ دائمًا من أول تاريخ متاح ونضيف يومًا واحدًا كل يوم (نستخدم البيانات اليومية). بهذه الطريقة يمكننا أن نرى كيف تتغير نتائج اختبار ADF بمرور الوقت. ولكن على عكس تيم ونيك، سنحدد إصدار اختبار ADF الذي سيتم تشغيله. وفقًا لويكيبيديا، تأتي اختبارات DF وADF بثلاث نكهات رئيسية:

الفرق بين هذه الإصدارات الثلاثة هو قدرتها على استيعاب (القضاء) على الاتجاهات المختلفة. يرتبط هذا بمتطلبات إنجل وجرانجر لإزالة أي اتجاهات حتمية - هذه الإصدارات الثلاثة قادرة على إزالة ثلاثة أنواع بسيطة من الاتجاهات الحتمية. يحاول الإصدار الأول وصف التغيرات اليومية في سعر السجل باستخدام بيانات سعر السجل السابقة فقط. يسمح الإصدار الثاني باستخدام مصطلح ثابت، مع تأثير أن log_price يمكن أن يكون له اتجاه خطي (إما لأعلى أو لأسفل). الإصدار الثالث يسمح بالمكونات التربيعية (المكافئة).

لا نعرف ما هي الإصدارات التي يعمل عليها Tim وNick، ولكننا سنعمل على تشغيل الإصدارات الثلاثة جميعها.

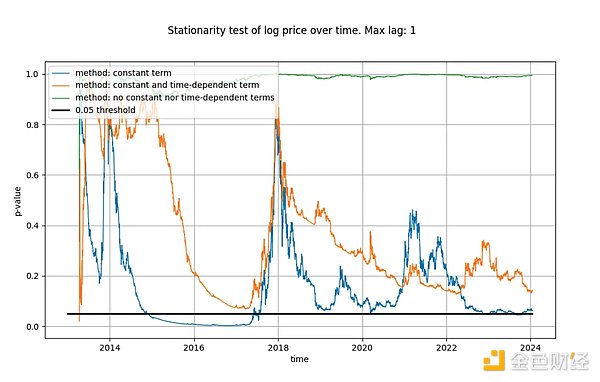
كان الحد الأقصى للتأخير الذي استخدمناه في اختبارات وحدة التغذية التلقائية للمستندات (ADF) لدينا هو 1، ولكن استخدام الفترات الزمنية الأطول لم يغير نتائجنا واستنتاجاتنا بشكل كبير. سوف نستخدم وظيفة statsmodels.tsa.stattools.adfuller الخاصة ببايثون، حيث يكون "maxlag" هو 1، وسنستخدم "n" و"c" و"ct" كمعلمات "انحدار" (أي ما يعادل المعلمات الثلاثة الموصوفة في ويكيبيديا أعلاه) ). في الشكل أدناه، نعرض القيمة p (مقياس للأهمية الإحصائية) التي يتم إرجاعها بواسطة الاختبار، حيث تعني القيم الأقل احتمالًا أعلى للثبات (عادةً ما يتم استخدام عتبة 0.05).

p>

نلاحظ أن النمط الأول (الخط الأخضر) يخلص بوضوح إلى أن السلسلة الزمنية log_price غير ثابتة. وهناك نسخة ثالثة من الاختبار (الخط البرتقالي) تؤدي إلى نفس النتيجة، ولكنها أقل حسما. ومن المثير للاهتمام أن الاختبار الذي يأخذ في الاعتبار حدًا ثابتًا (الخط الأزرق) لا يمكنه تحديد ما إذا كانت السلسلة الزمنية ثابتة (على الأرجح استخدم تيم أيضًا اختبار ADF بمصطلح ثابت). لماذا تختلف هذه الإصدارات الثلاثة كثيرًا، وعلى وجه الخصوص لماذا لا يستبعد الإصدار ذو المصطلح الثابت log_price من أن يكون ثابتًا؟

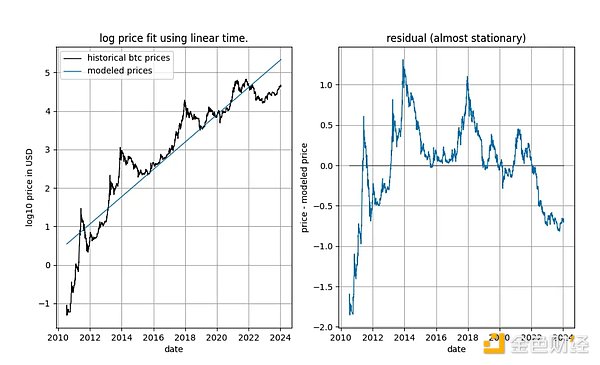
لا يمكن أن يكون هناك سوى تفسير واحد: استخدام مصطلح ثابت فقط في فرق log_price (مما يؤدي إلى مصطلح خطي في log_price) يناسب السلسلة الزمنية "جيدًا"، وينتج عن هذا إشارة متبقية تبدو ثابتة تقريبًا (على الرغم من وجود انحرافات كبيرة في البداية والنهاية). حتى الآن، لم يكن استخدام الاتجاه الحتمي على الإطلاق في log_price، أو استخدام التأثير الحتمي التربيعي، ناجحًا.

p>

يعطينا هذا بالفعل تلميحًا قويًا بوجود علاقة بين الوقت وlog_price. في الواقع، إذا خلص اختبار ADF باستخدام مصطلح ثابت إلى أن الإشارة ثابتة، فإن هذا يعني أن المصطلح الزمني الخطي قادر على تقريب log_price بشكل جيد بما يكفي للحصول على بقايا ثابتة. يعد الحصول على المخلفات الثابتة أمرًا مرغوبًا فيه لأنه علامة على وجود علاقة غير زائفة (أي أننا وجدنا المتغيرات التفسيرية الصحيحة). الاتجاه الزمني الخطي ليس ما نحتاجه تمامًا، ولكن يبدو أننا قريبون جدًا.

تختلف استنتاجاتنا بشكل كبير عن استنتاجات مارسيل بيرج، الذي ذكر (في مقال آخر):

"في تحليل سابق، أوضحت أن سعر البيتكوين كان جزءًا لا يتجزأ من الطلب الأول، ولا يزال كذلك. إن تطور الأسعار مع مرور الوقت لا يؤثر على البيتكوين. يُظهر أي عناصر حتمية."

نستنتج أن الوقت الخطي لا يفسر بشكل كامل حركة سعر البيتكوين مع مرور الوقت، ولكن من الواضح تمامًا أن log_price قد تم عنصر الوقت الحتمي. علاوة على ذلك، ليس من الواضح ما إذا كان log_price هو I(1) بعد إزالة المكونات الحتمية المناسبة (كما هو مطلوب من قبل Engel وGranger). وبدلا من ذلك، يبدو أن الاتجاه ثابت، ولكن لا يزال يتعين العثور على العنصر الحتمي المناسب.

إذا كنا نبحث عن التكامل المشترك، فإن حقيقة أن log_price ليس I(1) تمثل مشكلة بالفعل، لأنه لكي يتم التكامل المشترك بين متغيرين، يجب أن يكونا جميعًا هل أنا (1) أو أعلى.

متغير وقت السجل

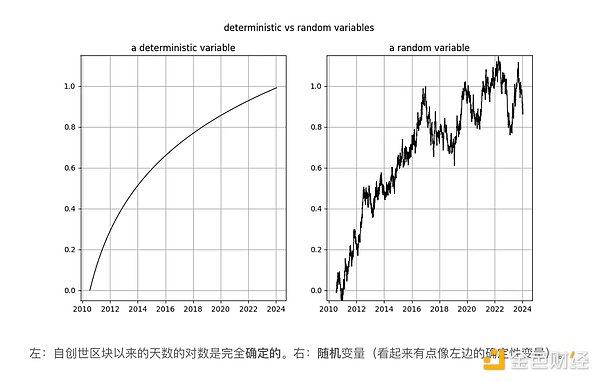
الآن دعونا نلقي نظرة على متغير log_time. استنتج مارسيل برجر أن log_time يبدو أنه جزء لا يتجزأ من الدرجة السادسة (احتفظ بالفرق حتى واجه مشاكل عددية). كانت الطريقة التي توقع بها أن تتحول دالة رياضية مثل اللوغاريتم من متغير حتمي تمامًا إلى متغير عشوائي أمرًا سخيفًا.

توصل نيك إلى نفس النتيجة بالنسبة لمتغيري log_time وlog_price: فهو بلا شك غير ثابت وبالتالي I(1) أو أعلى. يدعي تيم ستولت أن log_time غير ثابت من خلال البناء. هذه تصريحات مفاجئة! يشير النظام التكاملي والتكامل المشترك إلى مفهوم المتغيرات العشوائية وإزالة أي اتجاهات حتمية منها (انظر إنجل وجرانجر [2] أعلاه). وللتذكير: قيم المتغيرات الحتمية معروفة مسبقا، في حين أن قيم المتغيرات العشوائية ليست كذلك. الوقت (من الواضح) حتمي تمامًا، وكذلك الدالة اللوغاريتمية، لذا فإن log_time هو أيضًا حتمي تمامًا.

p>

إذا اتبعنا Engle وGranger وقمنا بإزالة الاتجاه الحتمي من log_time، فسيتبقى لدينا متجه من الأصفار لأن log(x) — log( x) = 0، أي أنه لا يزال لدينا إشارة حتمية تمامًا. هذا يعني أننا عالقون - لا يمكننا تحويل المتغير الحتمي تمامًا log_time إلى متغير عشوائي، لذلك لا يمكننا استخدام إطار عمل Engle وGranger.

هناك طريقة أخرى لفهم مدى إشكالية المتغير الحتمي تمامًا في تحليل التكامل المشترك وهي النظر في كيفية تعامل اختبارات الثبات (مثل اختبار ديكي فولر) معه. دعونا نفكر في أبسط حالة (حيث y هو المتغير محل الاهتمام، وrho هو المعامل الذي سيتم تقديره، وu هو مصطلح الخطأ المفترض أنه ضوضاء بيضاء):

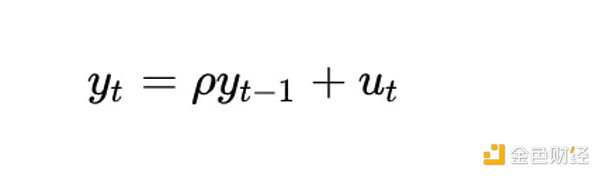
وينبغي أن حدث ما؟ مصطلح الخطأ u_{t} هو 0 لجميع قيم t لأنه ليس لدينا مكونات عشوائية - ليست هناك حاجة إلى خطأ. ولكن بما أن log_time هي دالة غير خطية للوقت، فإن قيمة rho يجب أن تعتمد أيضًا على الوقت.

بالنسبة للمتغيرات العشوائية، يعد هذا النموذج أكثر فائدة لأن المتغير rho يلتقط درجة ذاكرة القيم العشوائية السابقة. ولكن بدون قيم عشوائية، فإن النموذج لا معنى له.

تعاني أنواع أخرى من الاختبارات من نفس المشاكل التي تعاني منها المتغيرات الحتمية.

لذلك فإن المتغيرات الحتمية تمامًا لا تنتمي إلى تحليل التكامل المشترك. أو بمعنى آخر: تحليل التكامل المشترك لا يعمل مع الإشارات الحتمية، وإذا كانت إحدى الإشارات حتمية، فإن تحليل التكامل المشترك هو أداة عفا عليها الزمن لادعاء العلاقات الزائفة.

ماذا علي أن أفعل؟

يتم تعريف التكامل المشترك فقط بين متغيرين كلاهما I(d)، حيث d يساوي 1 على الأقل. لقد أظهرنا أن log_time متغير حتمي تمامًا ولا يمكن استخدامه في اختبارات الاستقرار. لا يمكننا أن نقول ما إذا كان log_time هو I(0) أو I(1) أو I(6). بالإضافة إلى ذلك، log_price ليس I(1)، ولكنه ذو اتجاه ثابت.

هل تعني حقيقة عدم وجود تكامل مشترك محدد بين log_time وlog_price أن قوانين القوة المستندة إلى الوقت غير صالحة إحصائيًا أو زائفة؟

من الصحيح تمامًا استخدام مزيج من المتغيرات الحتمية وثابتة الاتجاه في أي تحليل إحصائي مناسب. وكما يود منتقدونا أن يعتقدوا، فإن التكامل المشترك ليس هو النقطة المركزية في تحليل العلاقات الإحصائية.

لذا فالتكامل المشترك مستحيل. لكن تحليل السكونية ربما لا يزال له مكان عند تطبيقه على نماذج قانون القوى. دعونا نستكشف هذا أكثر.

السبب وراء قيامنا أولاً بإجراء تحليل التكامل المشترك بين متغيرات الإدخال هو أننا نأمل في العثور على مجموعة خطية ثابتة من الاثنين. لا يوجد سبب أساسي لعدم إمكانية الجمع بين المتغير الحتمي (log_time) ومتغير الاتجاه الثابت (log_price) للحصول على متغير ثابت. لذلك، بدلاً من البحث عن التكامل المشترك بالمعنى الدقيق للكلمة (نظرًا لأن المتبقي هو مجرد مزيج خطي من إشارتي الإدخال)، يمكننا ببساطة إجراء اختبار الثبات على البقايا. إذا كانت البقايا ثابتة، فسنجد تركيبات خطية ثابتة (وهذا هو هدف التكامل المشترك) حتى لو لم نتبع بدقة اختبار التكامل المشترك إنجل-جرانجر.

دراسة أعمق

جيمس ج. ماكينون في ورقته "اختبار التكامل المشترك وقد تم شرح ذلك بدقة في "القيمة الحرجة لـ "[3]: اختبار التكامل المشترك (اختبار Engle Granger) هو نفس اختبار ثبات البقايا (اختبار DF أو ADF). إذا كان انحدار "التكامل المشترك" "(استبدل انحدار log_time المرتبط بـ log_price) تم تنفيذها:

كرر ماكينون هذه العبارة: إذا كانت المعلمات التي تربط log_time وlog_price معروفة مسبقًا، فيمكنك تخطي التكامل المشترك لـ Engle Granger اختبار، وبدلاً من ذلك قم بإجراء أحد الأنماط الثلاثة الشائعة لاختبارات الاستقرار (اختبارات DF أو ADF) على المتبقي:

لذلك يمكننا استخدام إحدى الطريقتين، وهما متطابقة باستثناء إحصائية الاختبار التي تم إنشاؤها:

1. تناسب وقت السجل مع سعر السجل وحساب المتبقي ( خطأ). واستنادًا إلى هذا المتبقي، احسب اختبار DF أو اختبار ADF أفضل. وتخبرنا الإحصائية الناتجة ما إذا كان المتبقي ثابتًا أم لا.

2. افترض أن log_time وlog_price هما I(1)، وقم بإجراء اختبار التكامل المشترك Engle-Granger. تخبرنا الإحصائيات الناتجة أيضًا ما إذا كانت البقايا ثابتة أم لا.

بالنسبة لاختبار ADF، استخدم وظيفة statsmodels.tsa.stattools.adfuller الخاصة ببايثون؛ وبالنسبة لاختبار Engle-Granger، نستخدم statsmodels .tsa.stattools.coint. بالنسبة لكلتا الوظيفتين، نستخدم النكهة التي لا تستخدم الثوابت (لا يوجد انحراف ثابت مع مرور الوقت) لأن المتبقي لدينا لا ينبغي أن يحتوي على انحراف ثابت مع مرور الوقت (وهذا يعني أنه بمرور الوقت، يبدأ النموذج في زيادة السعر أو انخفاضه).

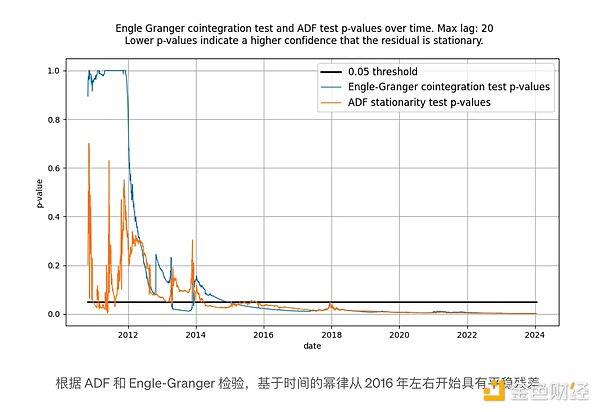
لقد كتبنا أن اختبارات ADF وEngle-Granger متكافئة، لكن هذا ليس صحيحًا تمامًا: فهما لا ينتجان نفس إحصائيات الاختبار. يفترض اختبار التكامل المشترك Engle-Granger أن N=2 متغيرين عشوائيين، بينما يفترض اختبار ADF أن N=1 متغير عشوائي (N هو مقياس درجات الحرية). يمكن أن يتأثر المتغير العشوائي بمتغير عشوائي آخر أو بمتغير حتمي، لكن المتغير الحتمي لا يمكن أن يتأثر بمتغير عشوائي. لذلك، في حالتنا (مع متغير حتمي واحد فقط log_time)، تُفضل الإحصائيات التي يتم إرجاعها بواسطة اختبار ADF (بافتراض N = 1 متغيرات عشوائية). من حيث المبدأ، قد تكون اختبارات Engle-Granger وADF غير متسقة، ولكن من الناحية العملية، ليس هذا هو الحال بالنسبة للنماذج المستندة إلى الوقت. كما هو موضح في الشكل أدناه، فإن الاستنتاج هو نفسه: نحصل على ناقل متبقي ثابت.

p>

لا يشير أي من الاختبارين في البداية إلى بقايا ثابتة، وهو أمر طبيعي. ويرجع ذلك إلى وجود مكونات منخفضة التردد في الإشارة المتبقية، والتي قد يتم الخلط بينها وبين إشارات غير ثابتة. ومع مرور الوقت فقط، يتعافى المتوسط ​​المتبقي بشكل ملحوظ ويصبح ثابتًا بشكل فعال.

S2F وأسعار مؤشرات الأسهم طويلة الأجل

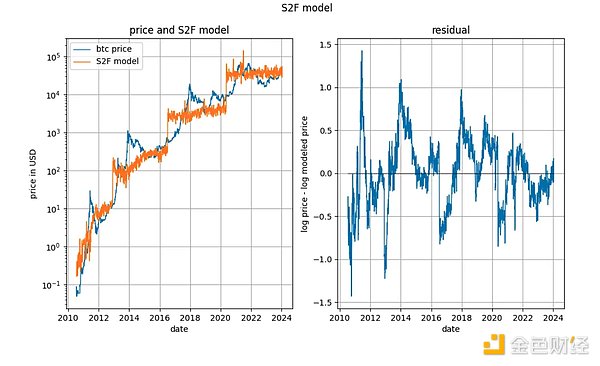
يبدو أن نموذج S2F كان بشكل عام تم تجاهله لأنه تبين أن التكامل المشترك الصارم مستحيل لسبب مشابه لسبب قوانين القوة المستندة إلى الوقت: (جزئيًا) متغيرات الإدخال الحتمية. ومع ذلك، فإن البقايا التي ينتجها النموذج تبدو مستقرة للغاية.

p>

في الواقع، كل من اختبار التكامل المشترك Engle-Granger واختبار ثبات ADF (المفضل نظرًا لوجود متغير حتمي ومتغير عشوائي) ينتج عنه p قريب جدًا من 0 قيمة. لذلك، لا ينبغي استبعاد أساس "الافتقار إلى التكامل المشترك" لنموذج S2F (والذي يعني في الواقع "الافتقار إلى الثبات").

ومع ذلك، فقد أشرنا في أوائل عام 2020 إلى أن هناك دلائل أخرى على أن نموذج S2F لا ينبغي أن يصمد. لقد ثبت أن توقعاتنا بأن سعر BTCUSD سيكون أقل من توقعات نموذج S2F كانت صحيحة.

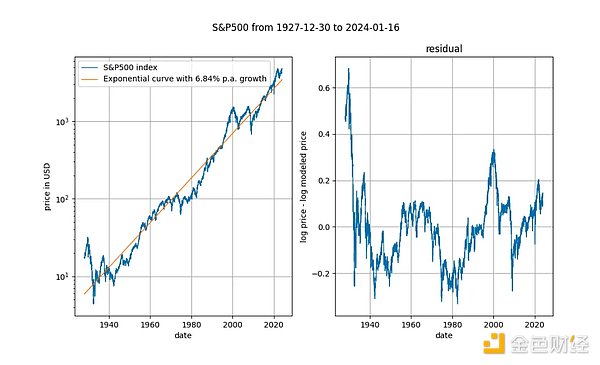
من المثير للاهتمام أيضًا النظر إلى مؤشرات أسعار الأسهم طويلة الأجل مقابل الوقت (هنا مؤشر S&P 500 بدون أرباح معاد استثمارها). ومن المعروف أن مؤشرات أسواق الأسهم الرئيسية تنمو بمعدل مؤشر متوسط ​​يبلغ حوالي 7%. في الواقع، نحن نؤكد ذلك من خلال الانحدار الأسي.

p>

هنا مرة أخرى لدينا متغير حتمي (الوقت). ينتج عن اختبار التكامل المشترك Engle Granger قيمة p تبلغ حوالي 0.025، وينتج اختبار ADF (المفضل) قيمة p تبلغ حوالي 0.0075 (لكن هذه القيم تعتمد بشكل كبير على الفترة الزمنية المحددة المختارة). مرة أخرى، بقايا ثابتة. الاتجاهات الزمنية الأسية في أسعار الأسهم صالحة.

التأثير

تم تطوير نموذج S2F في الأصل لأساسه الاقتصادي القياسي الجيد (خاصة الارتباط (خاصة مارسيل برجر ونيك إمبلو). عندما انقلب الوضع واكتشف أن نموذج S2F لا يمكن أن يوجد للتكامل المشترك (بالمعنى الدقيق للكلمة)، قفز كل من مارسيل ونيك من السفينة وأعلنا أن نموذج S2F غير صالح. يبدو أنه بعد هذا الحادث، تغيرت آراء الناس حول نموذج S2F أيضًا. لدى إريك وول ملخص قصير رائع لتطور الأحداث.

لقد أوضحنا، وتوافقنا مؤلفات الاقتصاد القياسي (ماكينون [3]) على أن التكامل المشترك والثبات قابلان للتبادل تقريبًا (باستثناء القيم الإحصائية). باستخدام هذه الرؤية، نجد أن نموذج S2F ليس لديه أي مشاكل مع التكامل المشترك/الثبات، لذلك سيكون من الخطأ تغيير رأي المرء بشأن نموذج S2F بسبب الافتقار المفترض للتكامل المشترك. نحن نتفق على أن نموذج S2F خاطئ، لكنه خاطئ لأسباب أخرى غير الافتقار إلى التكامل المشترك.

تعرض قانون القوة المستند إلى الوقت في البيتكوين لانتقادات بسبب افتقاره إلى التكامل المشترك، ويُزعم أنه وصف العلاقة بين log_time وlog_price بأنها زائفة. لقد أظهرنا أن قانون القوة القائم على الزمن في البيتكوين يحتوي على بقايا ثابتة على ما يبدو، وبالتالي فإن المنطق الذي يتبناه منتقدونا ليس له أي معنى.

يعتبر نموذج قانون السلطة المعتمد على الوقت في البيتكوين فعالاً ومستقرًا وقويًا. كما هو الحال دائما.