Original title: Fully Homomorphic Encryption: Introduction and Use-Cases
Original author: Nicolas Gama and Sandra Guasch, SandBoxAQ
Translator: Faust, Geekweb3
This blog is a systematic introduction to fully homomorphic encryption (FHE), but we will not discuss the mathematical details in depth here, but mainly explain this technology from the perspective of basic mechanism design, so that readers can have a preliminary understanding of the basic operating logic of FHE, and introduce several main application modes of FHE.
When it comes to "encryption", the application scenarios that people first think of are usually static encryption and encryption in transit. The former encrypts the data and stores it in hardware devices, such as hard drives, mobile devices, or cloud-based servers. In this mode, only authorized people can view or rewrite the decrypted plaintext content. The purpose of encryption in transit is to ensure that data transmitted over the Internet can only be interpreted by designated people. Even if the data is transmitted through a public router or channel, the middleman cannot privately decrypt the plaintext.
Both scenarios above rely on encryption algorithms, and also provide additional guarantees for data integrity, that is, the data is not tampered with by middlemen during transmission, which is called "authenticated encryption":Once the data is encrypted, participants in the data transmission process cannot privately decrypt the plaintext (confidentiality), and no middleman can arbitrarily tamper with the original ciphertext (integrity/authenticity).
As for some scenarios of multi-party collaboration, some complex processing of ciphertext is required, which belongs to the category of privacy protection technology, and fully homomorphic encryption (FHE) is one of them. We can give an example of online voting:Suppose in a presidential election, voters can encrypt their voting results and submit them to an intermediary entity, which collects all voting results, calculates the number of votes for each presidential candidate, and finally announces only one final election result. Unfortunately, when we use the “authenticated encryption” scheme mentioned above, the middleman responsible for counting the votes must decrypt everyone’s votes in plain text before he can perform the task of counting the votes, which will expose everyone’s votes and make privacy impossible to protect. In theory, we can shuffle everyone’s votes (some electronic voting protocols do this), but unlike paper ballots, traditional cryptographic mechanisms have difficulty separating encrypted ballot data from the corresponding voter identity while ensuring data integrity (not being tampered with). In online voting schemes, we can add a hardware isolation wall around the middleman responsible for counting votes, such as a TEE (trusted execution environment). This technology makes it difficult for malicious attackers to interact with the counting program, but hardware-level vulnerabilities may allow the key to decrypt the ciphertext to be leaked from the TEE, and unlike errors contained in software, hardware design vulnerabilities cannot be easily fixed.
In summary, in order to deal with the above scenarios, we can introduce fully homomorphic encryption (FHE) technology. FHE is a special form of encryption scheme that allows function calculations to be performed directly on ciphertext without decrypting the ciphertext, and obtains the encrypted result of the function output, so that privacy can be protected.
In the FHE scenario, the mathematical structure of the function ? is public, so the processing flow of input ciphertext ? and output result ?(?) is public information and can be executed in the cloud without leaking any privacy. It should be noted here that ? and ?(?) are both encrypted ciphertexts that need to be decrypted by a key. Most of the time, the decryption keys corresponding to the two are the same.
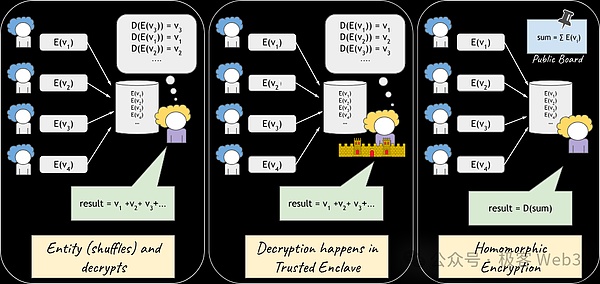
The above figure shows three encryption/decryption schemes for online voting, where E( ) represents encryption operations and D( ) represents decryption operations;
In the left figure, a trusted middleman will confuse and decrypt each voting data before announcing the voting results. We must assume that the middleman will not leak privacy and that the voting statistics are correct;
In the middle figure, TEE is used, which can ensure data integrity and privacy protection;
In the rightmost figure, homomorphic encryption is used: the encrypted voting data can be publicly summed up and then decrypted to get the final vote count
FHE (Fully Homomorphic Encryption) is a compact encryption scheme. The size of the ciphertext data of the output result ?(?) and the amount of work required to decrypt the result depend only on the original plaintext corresponding to the input data ?, and do not depend on the computational process used.This is very different from non-compact encryption systems, which often simply connect ? to the source code of the function ?, and then let the recipient decrypt ? and input it into ? to complete the computational task.
In reality, the FHE outsourcing model is often seen as an alternative to secure execution environments such as TEE.FHE's security is based on cryptographic algorithms, not on physical devices such as hardware. Therefore, FHE is completely unaffected by passive side-channel attacks or attacks on cloud servers. Imagine that someone needs to outsource some computing tasks, but the data is very sensitive. He may not want to use a virtual machine (VM) built on AWS, because there are often higher-level controllers behind such cloud-based servers. He may also be hesitant about things like SGX or TEE, because the host running the TEE can monitor the power consumption or running time generated by the computing task when it is executed, and may infer some information from these data.
However, if FHE is used, the person who outsources the computing task can rest assured - because in FHE systems, to crack private information, it is necessary to crack the cryptographic algorithm used, which is almost impossible to do at present.
However, while the cryptographic algorithm can prevent the attacker from cracking the plaintext corresponding to ? without knowing the key, on the other hand, universal malleability allows the attacker to modify the output result ?(?), which is equivalent to an active side channel attack: the attacker can carry out targeted attacks on the hardware executing the encryption algorithm to affect the output result. This may sound scary, but in the design of FHE, such malicious attacks can be circumvented by creating redundancy in the computation process.
To summarize briefly, FHE usually uses several sets of keys, including the following parts:
Decryption Key: This is the master key in the entire FHE encryption system, and all other types of keys can be derived from the master key. The decryption key is usually generated locally by the user and never transmitted to the outside world. Only the holder can use it to decrypt the FHE ciphertext. This means that even if the ciphertext is intercepted by others during transmission, it cannot be decrypted unless they have the decryption key.
Encryption Key: In the public key mode of FHE, the encryption key is the key used to convert plaintext into ciphertext. When the person who generates the initial ciphertext is not the holder of the decryption key/master key, the encryption key is used for encryption. This key is usually of medium size and consists of some random zero encryption. Since FHE supports affine functions, it is sufficient to encrypt any message.
In the public key encryption mode, the encryption key is usually public and anyone can use it to encrypt data, but only the holder of the decryption key can decrypt it specifically.
Evaluation Key: The evaluation key is a special key used to perform homomorphic operations on the ciphertext ?, allowing the FHE system to perform homomorphic operations on the ciphertext without decrypting the ciphertext ?. The evaluation key can be publicly released like a public key. Even if others know the evaluation key, they cannot crack the ciphertext ?, but can only perform homomorphic operations on the ciphertext to obtain an output result.
In addition, when the computation key is used for calculation, the structure of the ciphertext remains unchanged, and the result of the homomorphic operation on the ciphertext ? will be re-encrypted into a new ciphertext, which ensures the privacy of the calculation process and does not leak confidential data even if the calculation process is public.
Among the holders of the above-mentioned keys, the holder of the decryption key/master key is the most sensitive. He must ensure that the execution chain/process of the entire homomorphic operation is valid and correct, and the final ciphertext is secure, and then decrypt it to get the plaintext result. If malicious operations are introduced into the operation chain of FHE, the decryption key may be leaked during decryption. Fortunately, homomorphic operations can be performed publicly and verified by anyone.
Specific scenarios/modes of FHE
In this section, we will describe some common scenarios/modes in FHE and discuss the advantages and disadvantages of each mode.
Outsourcing Mode

In this figure, the orange key symbol on the left represents the decryption key (and its holder Alice). The FHE ciphertext is represented by a lock of the same color as the decryption key. The party that contributes private data is represented by a cylinder:
Here, only Alice contributed private data. On Bob's side, the homomorphic computing function and computing key are public, and the computing scheme is represented by a green box, which is carried out in a deterministic way. Everyone can rerun the computing process locally and check whether the output result given by Bob is wrong.
The above outsourcing model is also the first historical application case of FHE, which aims to transform ordinary cloud computing into private computing similar to SGX and TEE, but the security of the above FHE algorithm is based on cryptographic algorithms rather than hardware-level security measures.In this setting, Alice has some private data, but her computing power is limited, Bob has a cloud server with powerful computing power, and Bob does not contribute any additional private data.
Alice can encrypt the input parameters of the computing task ?(), get the ciphertext ? and send it to Bob, who then calculates the result of ?(?) in a homomorphic encryption way and sends the encrypted result back to Alice.
Given the current performance of hardware devices, the actual promotion of the FHE outsourcing model is relatively slow - if the complexity of the computational task ?() to be performed is nonlinear, the time required to perform FHE operations on ?() will reach 1 million times that of the original computation, and the memory overhead will increase by about 1,000 times. Many organizations are currently developing FHE-specific hardware to reduce its computational costs, such as the Darpa DPRIVE project or CryptoLight.
Currently, the FHE outsourcing model is actually mainly used in PIR (Private Information Retrieval) scenarios, where the public server controller Bob has a large public database, and the client Alice will initiate a request to read the data, but does not want Bob to know whose data she wants to check. This type of PIR scenario benefits from the linearity and compactness of homomorphic encryption operations, while the computational cost can be kept within a reasonable range.
The following table summarizes the advantages and disadvantages of the FHE outsourcing model.

Two Party Computing Mode (Two-Party Computing Mode)

The figure uses the same color settings as before. This time, Bob contributes some private data to the computation process. The computation process on Bob's side is no longer publicly verifiable, as indicated by the red box. This mode should only be limited to scenarios where both parties are honest-but-curious:
That is, during the execution of the protocol, participants (such as Bob) will strictly follow the given steps to perform the computation, and will not intentionally output incorrect results or disrupt the execution of the protocol. But Bob is "curious" and will try to infer sensitive information from the ciphertext or other intermediate data he comes into contact with, but this will not tamper with the execution of the protocol
In the FHE two-party computation mode, the only difference is that Bob will contribute some private data during the computation process, that is, add his own private data to the FHE computation process.In this case, FHE is a good two-party computation solution with minimal communication complexity, and can provide strong guarantees through its mechanism design: Bob will not spy on Alice's private data, and Alice will not spy on Bob's private data.
A potential application case of this scenario is the "millionaire's problem" in cryptography. Suppose Alice and Bob are two millionaires who want to know who is richer, but don't want to let the other know how much assets they have. The solution to this problem is often used in real-world e-commerce application scenarios.

Aggregation Mode
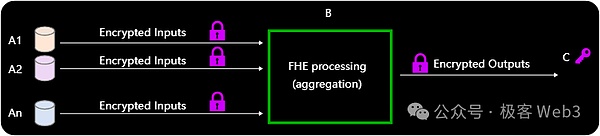
The aggregation mode is an improvement on the outsourcing mode, aggregating data from multiple participants in a compact (the output does not grow as the number of input parameters increases) and publicly verifiable way. Typical use cases include federated learning and online voting systems.
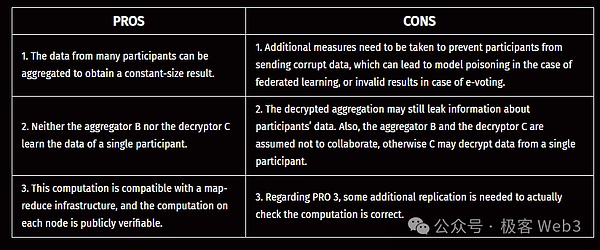
Client-Server Mode
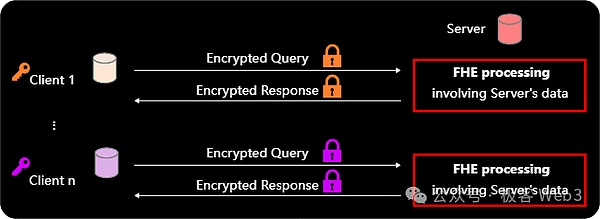
This mode is an improvement on the two-party computing mode mentioned above, in which the server provides FHE computing services to multiple clients with independent keys. FHE can be used for private AI model computing services, for example, the client has private data and the server has a private AI model or service). The private AI model owned by the server is stored locally in plain text, and then each client has its own private data that it wants to put into the AI model for computing. Finally, each client can use its own key to parse the result of the operation of the data it submitted.

Other details about homomorphic encryption
How does homomorphic encryption ensure that the external calculation results are valid?
It is easier to use FHE in a multi-party collaboration scenario because each participant has an incentive to honestly follow the protocol. For example, FHE can perform encrypted calculations and statistics between two legal entities located in two different countries but belonging to the same company/organization:Regulations such as GDPR allow you to publish certain statistics externally, but prohibit the storage of all personal data in the same physical location.
In this case, it is feasible to use FHE, and all participants have an incentive to honestly follow the protocol. In scenarios where the parties are not cooperating with each other, the simplest way to ensure that the computation has been performed correctly is to introduce redundancy (similar to multi-signature/consensus). For example, in the outsourcing and aggregation scenarios mentioned above, the function formulas used in homomorphic computation are completely public and can be deterministic. As long as two or more independent entities produce exactly the same output ciphertext, the entire computation process is correct and the result is credible. The higher the redundancy, the more credible the final result, but this requires a trade-off in efficiency.
In addition, when the contractor guarantees the validity of the FHE result by digitally signing the input and output ciphertext, everyone can rerun the same FHE computation process and check whether the proof given by the contractor is valid. Any cheating by the contractor can be detected and punished, and can be associated with a publicly verifiable certificate that reveals the cheating and the cheater - we call this model a strong hidden security model.
As for fully homomorphic signatures, it is another way to verify the correctness of calculations. It does not require a third-party verifier, but usually requires more software and hardware resources to participate.
How does FHE ensure that the final recipient only decrypts the final result rather than the intermediate variables?
The simplest way is to ensure that the holder of the decryption key cannot access the intermediate ciphertext generated in the FHE calculation process. In a two-party calculation scenario or a client-server scenario, Alice encrypts the input result, Bob calculates the ciphertext and transmits the encrypted output result back to Alice. Obviously, Alice can only decrypt the final result and cannot access the intermediate variables.
In cloud server-based scenarios, such as online voting systems, many participants will send encrypted voting data on public cloud servers such as AWS. Here, a method is used: The decryption key is usually not given to a single recipient, but is distributed to different people or institutions in a secret sharing manner (similar to MPC). In this case, only by performing multi-party computation and letting the members holding the decryption key communicate online can a specific ciphertext be decrypted. If some of them refuse to cooperate with others, decryption cannot be performed. In this way, the overall security of the system can be improved by setting the corresponding threshold.
Building blocks of homomorphic encryption
There are three types of homomorphic encryption: partially homomorphic encryption (PHE), hierarchical homomorphic encryption (LHE), and fully homomorphic encryption (FHE). Partial homomorphic encryption only allows us to perform homomorphic encryption on certain computing tasks (such as summation, linear functions, bilinear functions), while hierarchical homomorphic encryption and fully homomorphic encryption can support arbitrary computing tasks.
For LHE, the parameters used/generated by the system depend on the function calculation to be performed?(), and grow with the increase of the computational complexity of the function, which in turn leads to an increase in the size of the ciphertext and key, which consumes more storage and communication resources. The FHE scheme allows us to calculate any function that can be represented as a binary logic gate circuit under a given set of parameters (that is, a given key and ciphertext size). That is, unlike LHE, even if the task to be calculated becomes more and more complex, the parameters (as well as the key and ciphertext) involved in the FHE scheme will not become larger.
Therefore, FHE is the only mode that can ensure that the memory consumption and running time of homomorphic computation are proportional to the original plaintext/task. However, FHE has a technical problem: As the calculation continues, the noise (garbage data) contained in the ciphertext will increase. In order to avoid errors in the decryption result due to excessive noise, the FHE scheme will periodically perform a costly operation called bootstrapping, which can reduce the noise to a controllable level. We will introduce more and more about this in the future, so stay tuned!
Original link: https://cryptographycaffe.sandboxaq.com/posts/fhe-01/
 JinseFinance
JinseFinance
 JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance Cheng Yuan
Cheng Yuan JinseFinance
JinseFinance JinseFinance
JinseFinance Bitcoinist
Bitcoinist