ZK 기반 자산 증명

서론

우리는 중앙화된 거래소에서 암호화폐를 보유합니다. 중앙화된 거래소에서 거래하는 것은 매우 편리하고 빠르며, 비트코인 출시 이후 10년 동안 많은 중앙화된 거래소가 시장에 생겨나면서 사용자들이 암호화폐를 쉽게 사고 팔 수 있게 되었습니다. 하지만 중앙화된 거래소의 붐과 함께 사기와 악의적인 자금 세탁도 흔하게 발생하고 있습니다. 이에 니프티는 거래소의 갑작스러운 붕괴와 설립자의 미스터리한 죽음을 다룬 특별 홍보 영상 '아무도 믿지 마세요, 가상화폐 서스펜스 ^[1]'를 제작했습니다. 특히 2022년 FTX는 파산으로 파산 선고를 받아 전 세계에 충격을 주었고 많은 사용자와 펀드 회사에게 막대한 손실을 입혔습니다.

사실, 암호화폐 분야뿐만 아니라 다른 전통적인 분야에서도 회계 사기를 통해 투자자들을 속이는 일이 발생하고 있습니다. 21세기 초 전 세계를 뒤흔든 엔론 스캔들을 예로 들 수 있습니다. 엔론은 포춘지에서 6년 연속 '미국에서 가장 혁신적인 기업'으로 선정되었지만, 수천억 달러의 자산을 보유한 회사로 2002년 단 몇 주 만에 파산했습니다. 또 다른 예로 에버그란데는 건축에 배정된 자금을 다른 용도로 전용하여 결국 30년 모기지를 보유한 수많은 주택 소유자들이 집이 무너지기만을 기다리는 결과를 초래했습니다.

다양한 분야에서 사기가 확산되는 주요 원인 중 하나는 감사 및 회계 프로세스 자체가 완전히 공개적이고 투명하지 않아서 부패와 부정행위가 발생할 여지가 크다는 점입니다. 하지만 기업의 이익과 투자자의 프라이버시를 보호하기 위해 주요 재무 데이터는 완전히 공개되고 투명할 수 없기 때문에 규제를 강화하는 것 외에 금융 사기에 대한 대응은 좋은 해결책이 아니었지만, 영지식 증명 기술이 점차 성숙해지면서 새로운 해법을 찾을 수 있을 것으로 보입니다.

모든 사용자가 자산의 금융 사기 여부를 스스로 검증할 수 있다면, 사용자의 검증 규모가 충분히 크다면 금융 사기를 하려는 기관이 감당하기 어려운 난이도가 될 것입니다. 또한 검증 프로세스가 영 지식이기 때문에 검증 데이터가 네트워크를 통해 전송되므로 제 3자가 데이터를 가로 채더라도 사용자의 실제 자산이 무엇인지 알지 못하므로 검증 프로세스가 네트워크에 완전히 공개적으로 표시 될 수 있습니다. 영지식 증명 기술의 도움으로 상당수의 감사는 더 이상 빅4 회계법인과 같은 특정 기관의 전유물이 아니며, 비공개로 비밀리에 수행됩니다. 오히려 모든 이해관계자가 참여할 수 있는 공개적인 프로세스가 되었습니다.

Summa^[2]는 zk 접근 방식을 사용하여 사용자 자산 검증을 수행하는 것을 목표로 하는 PSE 연구 프로젝트입니다. 이 글의 나머지 부분에서는 프로젝트의 개요와 기술적 구현에 대해 설명합니다.

컨트랙트

서마의 전체 데이터 흐름은 다이어그램에 나와 있습니다. 스마트 컨트랙트는 주로 일부 공개 데이터 저장 및 검증에 사용됩니다. 반드시 이더에 묶여 있는 것은 아니며, 솔라나와 같은 다른 블록체인에 배포할 수 있습니다(Halo2가 블록체인을 지원하는 한, 이 프로젝트의 일부 계약은 Halo2 증명^[3]에 의해 생성됩니다).

도표에서 커스터디언은 중앙화된 교환을 나타냅니다. 계약은 거래소에 의해 체인에 배포되고, 계약 소유권은 거래소가 소유하며, 공개 데이터는 거래소에 의해서만 제출할 수 있습니다. 공개 데이터는 거래소가 관리하는 체인의 기본 정보와 디지털 서명의 두 부분으로 구성됩니다.

두 번째 부분은 머클 합 트리의 루트 해시, 루트 잔액 등 체인 내 자산에 대한 정보입니다( 두 번째 부분은 머클 합 트리의 루트 해시와 루트 잔액(체인에 있는 자산 수, 예: BTC 수)을 포함하여 체인에 있는 자산에 대한 정보이며, 이는 zk 증명을 위한 인스턴스 입력으로 사용됩니다.

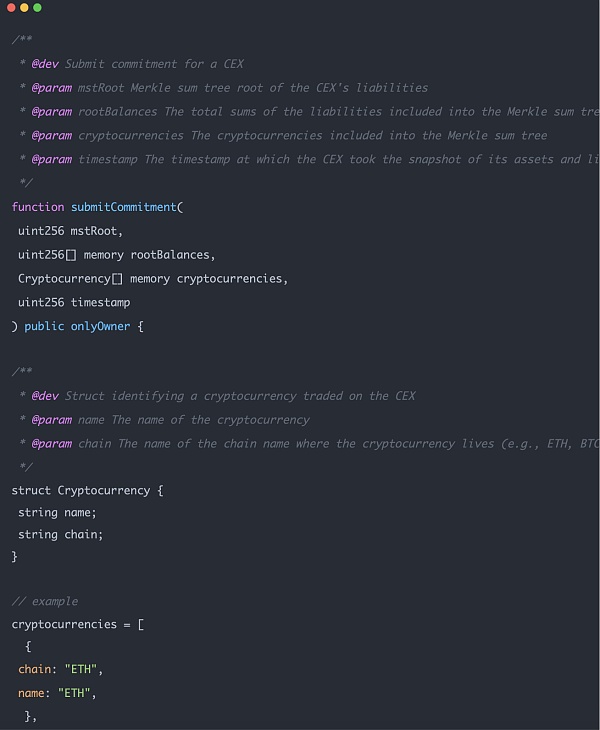
데이터의 이 두 부분은 온체인에서 쉽고 공개적으로 쿼리가 가능합니다(루트 해시는 제외). 거래소가 이 데이터를 속이는 것은 매우 어렵습니다. 누구나 컨트랙트에 저장된 데이터와 블록체인 주소의 실제 데이터 결과를 비교할 수 있습니다.

증명 생성은 현재 거래소에서 생성합니다. 사용자가 검증이 필요한 주요 정보를 거래소에 제출하면 거래소는 증명을 생성하여 사용자에게 반환합니다. 그러면 사용자는 이 증명을 가져와 스마트 콘트랙트에 요청하면 스마트 콘트랙트는 증명을 검증합니다.

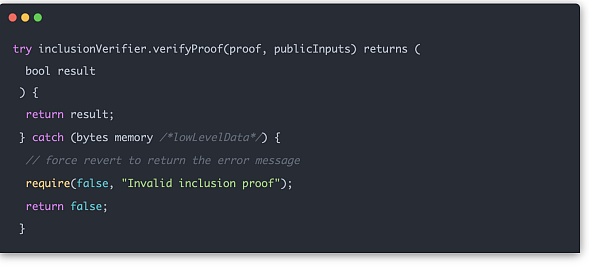
마지막으로, 증명 검증은 사용자와 콘트랙트 간의 직접적인 상호 작용입니다. 이 부분은 Halo2 회로에 의해 솔리디티 코드로 변환된 다음 별도의 검증 콘트랙트로 체인에 배포됩니다.

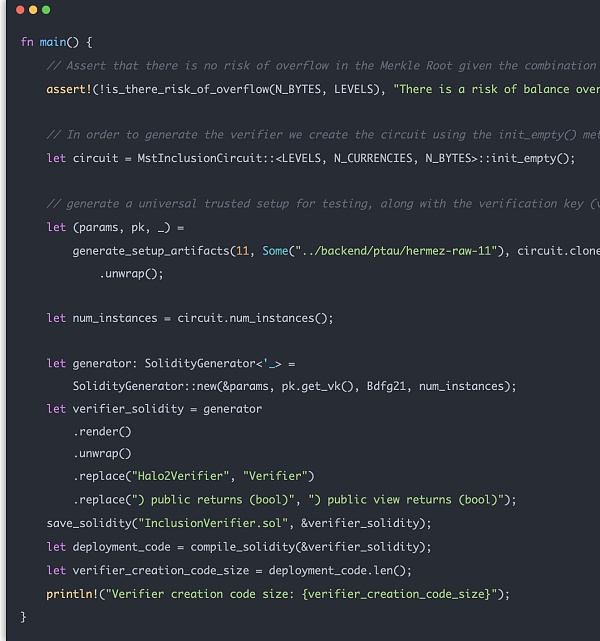
실제 사용 시 체인에서 증명 전달을 통해 계산 및 검증이 가능합니다.

다음 코드 예시는 실제 사용된 해시 함수이며, 전체 해시 연산 자체에 비트 연산이 사용되지 않고 덧셈과 곱셈만 사용되는 것을 볼 수 있습니다. 덧셈과 곱셈만 사용하므로 zk 친화적입니다.

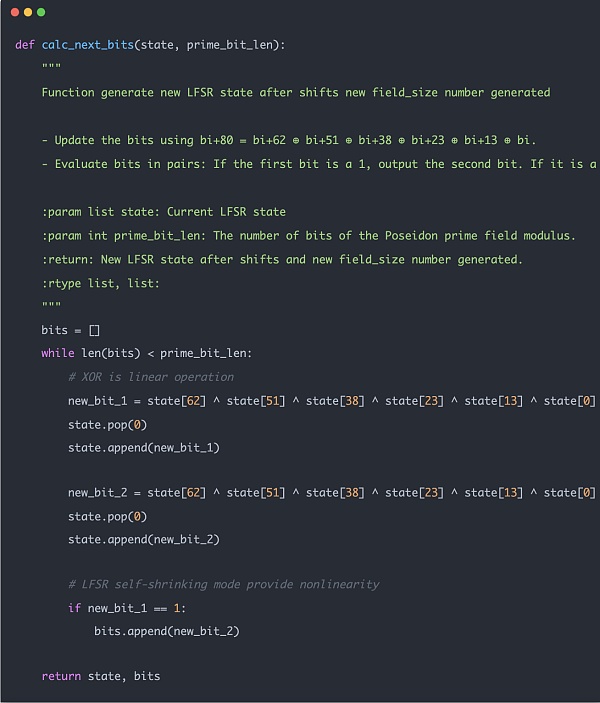
zk 데이터 계산은 유한한 영역에서 계산해야 한다는 점에서 기존의 절차적 계산과 다르며, 머클 트리 구축 시 각 노드의 데이터가 유한한 영역을 넘지 않도록 해야 합니다. 머클 트리를 구축할 때 각 노드의 데이터가 유한 도메인을 넘지 않도록 해야 하며, 이를 위해 계산 전에 범위 검사를 수행하여 오버플로를 방지합니다.

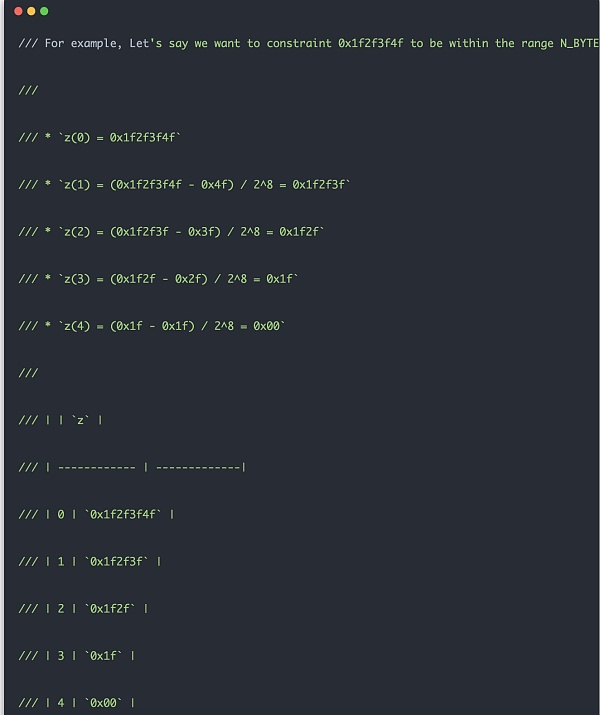
범위 검사의 일반적인 원리는 다음 예시와 유사합니다. 우선 입력 데이터를 8비트 길이 단위로 잘라내어 향후 뺄셈 연산을 쉽게 할 수 있도록 합니다. 그리고 다음 값을 계산할 때마다 아래 예시와 같이 계산합니다. 범위 검사 회로는 실제로 diff = z_cur - z_next * Expression::Constant(Fp::from(1 << 8))라는 중간 결과에 의해 제약을 받으므로 diff = z_cur - z_next * Expression::Constant(Fp::from(1 << 8))는 중간 결과의 제약이 있어야만 합니다. 코드>를 사용하여 제약 조건을 수행하려면 차이가 8비트 값 이내여야 합니다. 이런 식으로 32비트 데이터 제약 조건의 경우 계산 셀 4개와 룩업 테이블 256개만 차지하면 되고, 가장 높은 비트가 0인 인스턴스 제약 조건을 사용할 수 있습니다. 그렇게 설계되지 않은 경우 32 비트 값 범위 검사를 수행하고 조회 테이블의 크기가 필요하며 분명히 이러한 회로가 너무 커서 실제로 적용 할 수 없습니다.

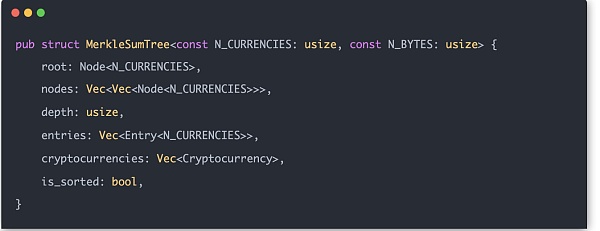
이러한 보조 구조가 준비되었으니 이제 머클 합 트리를 정식으로 구축할 차례입니다. 각 사용자 입력을 Entry라고 하며 다음과 같이 구조화됩니다:

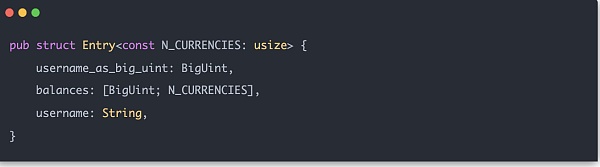
머클 트리의 중간 노드의 해시는 H(LeftChild.balance[0] +. RightChild.balance[0], LeftChild.balance[1] + RightChild.balance[1], ... , LeftChild.balance[N_CURRENCIES - 1] + RightChild.balance[N_CURRENCIES - 1], LeftChild.hash, RightChild.hash)이므로 계산할 vec 배열의 실제 길이는 <코드 >N_CURRENCIES + 2입니다.

이제 전체 머클 트리를 구축해 보겠습니다. 리프 노드는 간단하며, 엔트리를 노드로 변환하기만 하면 됩니다. 중간 노드는 레이어별로 구성해야 하며 각 중간 노드의 값은 다음 레이어의 왼쪽 및 오른쪽 하위 트리의 값과 관련이 있습니다. 마지막으로 계산된 중간 노드의 결과를 트리 배열에 넣습니다.

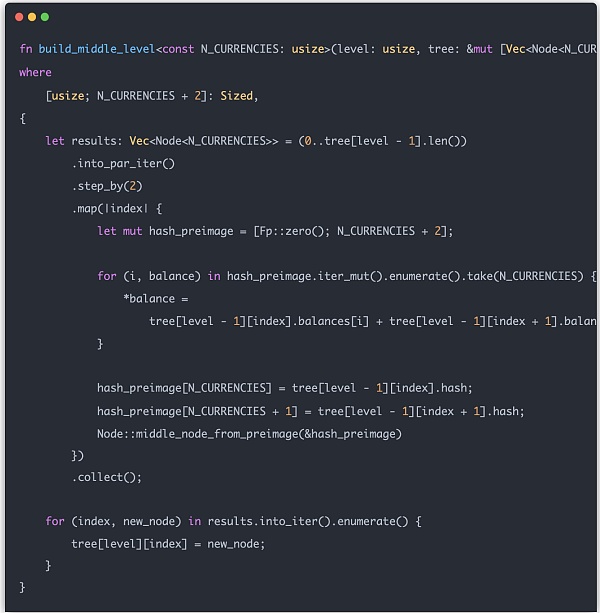
다음으로 머클 트리를 사용하여 zk 증명을 구축합니다. zk는 사용자의 항목이 실제로 해당 머클 트리에 있음을 증명합니다. 머클 트리. 따라서 먼저 특정 항목의 색인을 생성하고 머클 트리를 기반으로 zk 증명에 필요한 데이터 구조를 생성해야 합니다.

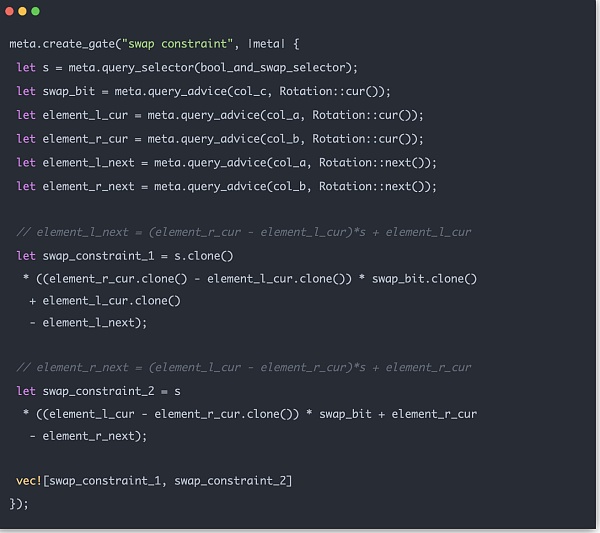
0과 1을 설정하여 전체 방정식을 0으로 만드는 제약 효과를 미묘하게 얻을 수 있습니다.

이미지 src="https://img.jinse.cn/7202784_image3.png" title="7202784" alt="oRyRD1H8D48iZx6fNgqte3C4aAV4ePLYIexfumrv.png">

머클 트리 zk 제약 조건에는 크게 두 가지 부분이 있는데, 하나는 거래소가 실제로 위 다이어그램의 실제 순서대로 증명을 생성하도록 보장하는 스왑 제약 조건입니다. 다른 하나는 잔액 제약 조건으로, 부모 노드의 잔액은 실제로 왼쪽 자식 노드와 오른쪽 자식 노드의 합에서 나온다는 것입니다. 잔액에 대한 합 제약 조건은 비교적 간단하므로 여기서는 스왑 제약 조건에 집중해 보겠습니다.

앞서 소개한 머클 zk 트리 데이터 구조 sibling_middle_node_hash_preimages는 배열이며, 위치 정보를 포함하지 않습니다. 그림에서 점선 상자의 위치가 트리의 왼쪽에 있는지 오른쪽에 있는지는 path_indices의 0과 1에 의해 결정됩니다. 따라서 값이 0이면 생성하는 부모가 왼쪽에 있고 같은 레벨에 해당하는 형제자매가 오른쪽에 있어야 하며, 값이 1이면 그 반대가 되어야 합니다. 이 로직은 데이터를 zk 회로로 가져올 때 코드에서 쉽게 구현할 수 있습니다.

전체 머클 합 트리 zk 증명 과정은 데이터를 레이어별로 처리한 다음 해당 위치 데이터를 zk 제약 회로에 입력하는 방식입니다. 확인합니다. 최종 출력은 루트 노드 해시와 총 잔액이며, 이는 컨트랙트의 해당 데이터와 일치해야 하며 인스턴스를 사용하여 일관성을 검증합니다. 모든 검증이 정상이라면 전체 머클 트리의 증명이 완료된 것입니다.

지불능력 검증

증명을 생성하는 과정은 사용자가 거래소에 요청하고, 거래소가 증명 데이터를 반환한 다음 사용자가 스마트 콘트랙트로 이를 검증하는 순서로 진행됩니다. 현재 해당 프로젝트는 거래소를 우회하는 사용자의 증명 생성을 지원하지 않지만, 향후 검토해 볼 수 있는 방향일 수 있습니다. 거래소가 증명을 반환하는 것이 아니라 사용자가 직접 증명을 생성하는 것입니다. 전체 halo2 증명 회로를 러스트를 사용하여 웹 어셈블리로 패키징한 다음, 해당 인터랙션 API를 이더를 사용하여 만들 수 있습니다. 머클 트리 루트 검증의 시간 복잡도는 로그(n)이므로 사용자 기기에서 검증을 수행하는 데 많은 시간이 걸리지 않아 탈중앙화의 보안이 더욱 강화될 수 있습니다. 이는 탈중앙화의 보안을 더욱 강화합니다.

참고자료

[1]

아무도 믿지 마세요, 가상 화폐 서스펜스: https://www. netflix.com/hk/title/81349029

[2]

Summa: https://github.com/summa-dev

[3]

Halo2 증명 생성됨: https://github.com/privacy-scaling-explorations/halo2- 솔리디티 검증자

[4]

포세이돈 해시: https://github.com/ingonyama-zk/ 포세이돈 해시

[5]

파라미터 준비 단계 및 해시 연산 단계: https://autoparallel.github.io/ overview/index.html

[6]

선형 피드백 시프트 레지스터: https://en. wikipedia.org/wiki/Linear-feedback_shift_register

[7]

ethers rs: https:/. /github.com/gakonst/ethers-rs

추천 자료

ZK 인사이트 시리즈

ZKP 연구 노트

Wen Building 팟캐스트

연구 분석 시리즈

유니스왑 파인 플립 시리즈

안탈파 랩스(Antalpha Labs)는 비영리 웹3 개발자 커뮤니티입니다. 오픈 소스 소프트웨어를 시작하고 지원함으로써 웹3.0 기술의 혁신과 채택을 촉진하는 데 전념하고 있습니다.

공식 웹사이트: https://labs.antalpha.com

트위터: https://labs.antalpha.com

트위터:

Twitter:

Youtube: https://www.youtube.com/channel/ UCNFowsoGM9OI2NcEP2EFgrw

문의처: [email protected]