Author: Vitalik, founder of Ethereum; Translator: Deng Tong, Golden Finance
Note: This article is the fourth part of the series of articles recently published by Vitalik, founder of Ethereum, on “The Future Development of the Ethereum Protocol”, “Possible futures of the Ethereum protocol, part 4: The Verge”. For the third part, see "Vitalik: Key Goals of Ethereum's The Scourge Phase", for the second part, see "Vitalik: How Should the Ethereum Protocol Develop in The Surge Phase", and for the first part, see "What Other Improvements Can be Made for Ethereum PoS". The following is the full text of Part 4:
Special thanks to Justin Drake, Hsiao-wei Wang, Guillaume Ballet, Ignacio, Josh Rudolf, Lev Soukhanov, Ryan Sean Adams, and Uma Roy for their feedback and review.
One of the most powerful features of blockchain is that anyone can run a node on their own computer and verify that the chain is correct. Even if 95% of the nodes running the consensus on the chain (PoW, PoS, ...) immediately agreed to change the rules and started producing blocks according to the new rules, everyone running a fully validating node would refuse to accept the chain. Stakeholders that do not belong to such a group will automatically converge and continue to build a chain that continues to follow the old rules, and fully validating users will follow that chain.
This is the key difference between blockchains and centralized systems. However, in order to maintain this property, running a fully validating node needs to be actually feasible for a critical mass of people. This applies both to stakers (as if stakers do not validate the chain, they are not actually contributing to enforcing the rules of the protocol) and to regular users. Today, it is possible to run a node on a consumer laptop (including the one used to write this article), but it is difficult to do so. The Verge aims to change this by making it so computationally cheap to fully validate the chain that every mobile wallet, browser wallet, and even smartwatch will do it by default.
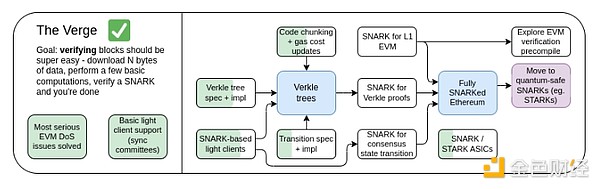
The Verge, 2023 roadmap.
Originally, "Verge" referred to the idea of moving Ethereum state storage to a Verkle tree - a tree structure that allows for more compact proofs, enabling stateless verification of Ethereum blocks. Nodes can validate Ethereum blocks without having any Ethereum state (account balances, contract code, storage, ...) on their hard disk, but at the cost of spending a few hundred kilobytes of proof data and a few hundred milliseconds of extra time to verify the proof. Today, Verge represents a larger vision focused on achieving maximum resource-efficient verification of the Ethereum chain, which includes not only stateless verification techniques, but also the use of SNARKs to verify all Ethereum executions.
Besides the long-term focus on SNARKs verifying the entire chain, another new question is related to whether Verkle trees are the best technique. Verkle trees are vulnerable to attacks by quantum computers, so if we replace the current KECCAK Merkle Patricia trees with Verkle trees, we will have to replace these trees again later. The natural alternative to Merkle trees is to jump straight to using STARK Merkle branches in a binary tree. Historically, this has been considered infeasible due to overhead and technical complexity. However, recently, we’ve seen Starkware prove 1.7 million Poseidon hashes per second on a laptop with Circle STARKs, and proof times for more “traditional” hashes are also decreasing rapidly thanks to technologies like GKR.
As a result, over the past year Verge has become more open to a multitude of possibilities.
The Verge: Key Goals
Stateless Clients: Fully validating clients and staking nodes should not require more than a few GB of storage.
(Long-term) Fully verify the chain (consensus and execution) on a smartwatch. Download some data, verify the SNARK, done.
In this post we will focus on the following:
Stateless Verification: Verkle or STARKs
Validity Proofs for EVM Execution
Validity Proofs for Consensus
Today, Ethereum clients need to store hundreds of GB of state data to verify blocks, and this amount continues to increase every year. The raw state data increases by about 30 GB per year, and individual clients must store some additional data in addition to being able to effectively update the trie.
This reduces the number of users who can run a fully validating Ethereum node: while hard drives are large enough to store all of Ethereum state and even years of history, the computers people buy by default tend to have only a few hundred gigabytes of storage. The state size also makes the process of setting up a node for the first time very cumbersome: the node needs to download the entire state, which can take hours or days. This has various knock-on effects. For example, it makes it much harder for stakers to upgrade their staking setup. Technically, this can be done without downtime — start a new client, wait for it to sync, then shut down the old client and transfer the keys — but in practice, it’s technically complicated.
Stateless validation is a technique that allows nodes to validate blocks without possessing the full state. Instead, each block comes with a witness that includes (i) the values of specific locations in the state that the block will access (e.g. code, balances, storage), and (ii) cryptographic proof that those values are correct.
Practically implementing stateless validation requires changes to the Ethereum state trie structure. This is because the current Merkle Patricia tree is extremely unfriendly to implementing any cryptographic proof scheme, especially in the worst case. This is true for both the “original” Merkle branch and the possibility of “wrapping” a Merkle branch in a STARK. The main difficulties stem from two weaknesses of MPT:
It is a hexagram tree (i.e. each node has 16 children).This means that on average a proof in a tree of size N is 32*(16-1)*log16(N) = 120*log2(N) bytes, or about 3840 bytes in a 232-item tree. For a binary tree, only 32*(2-1)*log2(N) = 32*log2(N) bytes are needed, or about 1024 bytes.
The code is not Merkelized.This means that providing any access to an account's code requires providing the full code, which has a maximum length of 24000 bytes.
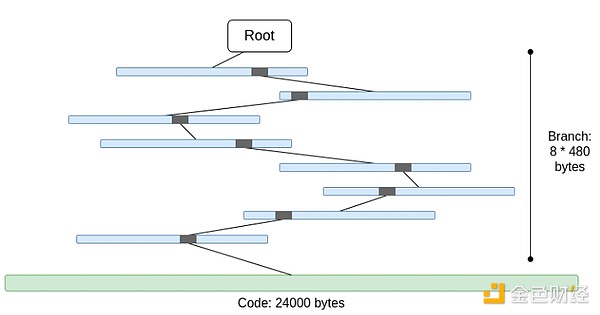
We can calculate the worst case as follows:
30,000,000 Gas / 2,400 ("cold" account read cost) * (5 * 480 + 24,000) = 330,000,000 bytes
The branch cost is slightly lower (5*480 instead of 8*480) because the top of the branch is repeated when the number of branches is large. But even so, the amount of data downloaded in one slot is completely impractical. If we try to wrap this in a STARK, we run into two problems: (i) KECCAK is relatively STARK-unfriendly, and (ii) 330 MB of data means we have to prove 5 million calls to the KECCAK round function, which is a way to go. Even if we can make STARK proofs KECCAK more efficient, there’s still a lot that can’t be proven on all but the most powerful consumer hardware.
If we just replace the hexatree with a binary tree, plus the Merkelize code, the worst case becomes about 30,000,000 / 2,400 * 32 * (32 - 14 + 8) = 10,400,000 bytes (~214 branches, where 8 is the length of the proof to go into a leaf). Note that this requires changing the gas cost to charge for accessing each individual block of code; EIP-4762 does just that. 10.4 MB is much better, but it's still too much data to download in a single slot for many nodes. So we need to introduce some more powerful techniques. There are two main solutions for this: Verkle trees and Starked binary hash trees.
Verkle trees use vector commitments based on elliptic curves to make shorter proofs. The key is that no matter how wide the tree is, the proof fragment corresponding to each parent-child relationship is only 32 bytes. The only limit on the width of the tree is that if the tree is too wide, the proof will be less computationally efficient. Ethereum's recommended implementation width is 256.
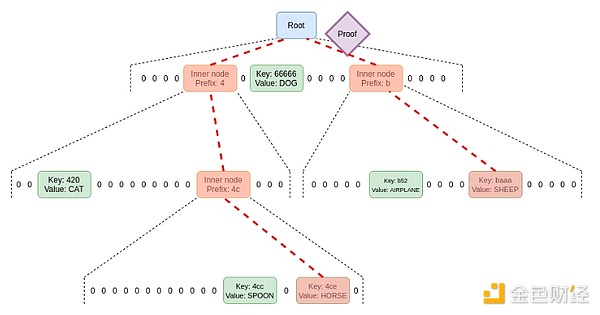
Thus, the size of a single branch in the proof becomes 32*log256(N) = 4*log2(N) bytes. The theoretical maximum proof size becomes about 30,000,000/2,400*32*(32-14+8)/8 = 1,300,000 bytes (the math is slightly different in practice due to uneven distribution of state blocks, but this is good as a first).
As an additional caveat, note that in all of the above examples, this "worst case" isn't really the worst case: a worse case would be for an attacker to deliberately "mine" two addresses to have a very long common prefix in the tree, and read from one of them, which can extend the worst-case branch length by about 2 more times. But even with this caveat, Verkle trees get us to a worst-case proof of about 2.6 MB, which roughly matches today's worst-case call data.
We also take advantage of this warning to do one other thing: we make it very cheap to access "adjacent" storage: many code blocks of the same contract, or adjacent storage slots. EIP-4762 provides a definition of adjacency, and adjacency accesses are charged just 200 gas. For adjacency accesses, the worst-case proof size becomes 30,000,000/200*32 = 4,800,800 bytes, which is still roughly within tolerance. If we want to lower this for safety, we can increase the cost of adjacency accesses slightly.
The technique here is pretty self-explanatory: you make a binary tree, take the max-10.4-MB proof you need to prove a value in a block, and replace that proof with a STARK of that proof. This lets us see that the proof itself only contains the data being proved, plus about 100-300 kB of fixed overhead for the actual STARK.
The main challenge here is proof time. We can do essentially the same calculation as above, except instead of counting bytes, we count hashes. A 10.4 MB block means 330,000 hashes. If we add the possibility of an attacker "mining" an address in the tree with a long common prefix, the true worst case becomes about 660,000 hashes. So if we can prove about 200,000 hashes per second, we'll be fine.
These numbers have been achieved on consumer laptops with the Poseidon hash function, which was specifically designed to be STARK-friendly. However, Poseidon is relatively immature, so many people don't trust its security yet. Therefore, there are two realistic paths forward:
Quickly perform a lot of security analysis on Poseidon, and get familiar with it enough to deploy it at L1
Use a more "conservative" hash function, such as SHA256 or BLAKE
At the time of writing, Starkware's STARK prover can only prove about 10-30k hashes per second on a consumer laptop if it is proving a conservative hash function. However, STARK technology is rapidly improving. Even today, GKR-based technology shows promise to push this to the ~100-200k range.
Besides validating blocks, there are three other key use cases that enable more efficient stateless validation:
Mempool:When a transaction is broadcast, nodes in the p2p network need to verify that the transaction is valid before rebroadcasting it. Today, validation involves not only verifying the signature, but also checking that the balance is sufficient and that the nonce is correct. In the future (e.g. with native account abstractions such as EIP-7701), this may involve running some EVM code that does some state access. If nodes are stateless, transactions will need to be accompanied by a proof that proves the state object.
Inclusion Lists:This is a proposed feature that would allow a (potentially small and unsophisticated) proof-of-stake validator to force the next block to include a transaction, regardless of the wishes of the (potentially large and complex) block builders. This would reduce the ability of powerful actors to manipulate the blockchain by delaying transactions. However, this requires that validators have a way to verify the validity of the transactions in the included list.
Light Clients:If we want users to access the chain through wallets (e.g. Metamask, Rainbow, Rabby...) without trusting centralized actors, they need to run a light client (e.g. Helios). The core Helios module provides users with a verified state root. However, in order to have a fully trustless experience, users need to provide proofs for each individual RPC call they make (e.g. for an eth_call request, the user needs proofs of all the states accessed during the call);
One thing all of these use cases have in common is that they require a fairly large number of proofs, but each proof is small. Therefore, STARK proofs don't really make sense for them; instead, using Merkle branches directly is most realistic. Another advantage of Merkle branches is that they are updatable: given a proof for a state object X rooted at block B, if you receive a child block B2 with its witnesses, you can update the proof to have it rooted at block B2. Verkle proofs themselves are also updateable.
What is the connection with existing research?
Verkle tree: https://vitalik.eth.limo/general/2021/06/18/verkle.html
John Kuszmaul’s original Verkle tree paper : https://math.mit.edu/research/highschool/primes/materials/2018/Kuszmaul.pdf
Starkware Proof Data: https://x.com/StarkWareLtd/status/1807776563188162562
Poseidon2 paper: https://eprint.iacr.org/2023/323
Ajtai (Alternative fast hash functions based on lattice hardness): https://www.wisdom.weizmann.ac.il/~oded/COL/cfh.pdf
Verkle.info: https://verkle.info/
The main work left to do is:
More analysis of the consequences of EIP-4762 (stateless gas cost changes)
More work completing and testing the transition procedures, which is a large part of the complexity of any stateless EIP
More security analysis of Poseidon, Ajtai, and other “STARK-friendly” hash functions
Further development of ultra-efficient STARK protocols for “conservative” (or “traditional”) hash functions, such as those based on Binius or GKR’s ideas.
We will soon reach a decision point on which of the three options we choose: (i) Verkle trees, (ii) STARK-friendly hash functions, and (iii) conservative hash functions. Their properties can be roughly summarized in the following table:
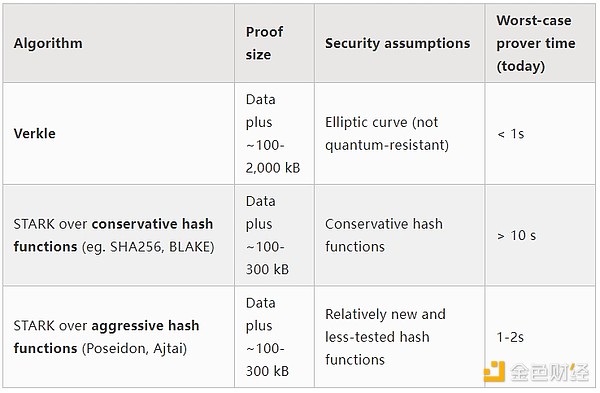
Besides these “headline numbers”, there are some other important considerations:
The Verkle tree code is fairly mature these days. Using anything other than Verkle would actually delay deployment, most likely via a hard fork. This might be okay, especially if we need extra time for hash function analysis or prover implementation anyway, and if we have other important features we want to include in Ethereum sooner rather than later.
Updating the state root using a hash is faster than using a Verkle tree. This means that hash-based approaches can improve full node sync times.
Verkle trees have an interesting witness update property - Verkle tree witnesses are updatable. This property is useful for memory pools, containment lists, and other use cases, and it may also help make the implementation more efficient: if you update a state object, you can update the witness of the second-to-last level without even reading the last level.
Verkle trees are harder to SNARK prove. If we want to reduce the proof size all the way down to a few kilobytes, Verkle proofs present some difficulties. This is because the verification of Verkle proofs introduces a large number of 256-bit operations, which requires the proof system to either have a lot of overhead or itself have a custom internal structure containing the 256-bit part for the Verkle proof.
If we want the updatability of Verkle witnesses to be done in a quantum-safe and reasonably efficient way, another possible path is to use a grid-based Merkle tree.
If the proof system is not efficient enough in the worst case, we can use another "rabbit in the hat" to make up for this deficiency, which is multi-dimensional gas: having separate gas limits for (i) calldata, (ii) computation, (iii) state access, and possibly other different resources. Multidimensional Gas increases complexity, but in exchange it more tightly constrains the ratio between average and worst case scenarios. With multidimensional Gas, the theoretical maximum number of branches to prove could be reduced from 30,000,000 / 2400 = 12,500 to 3000. This would make BLAKE3 (barely) sufficient even today, without further proof improvements.
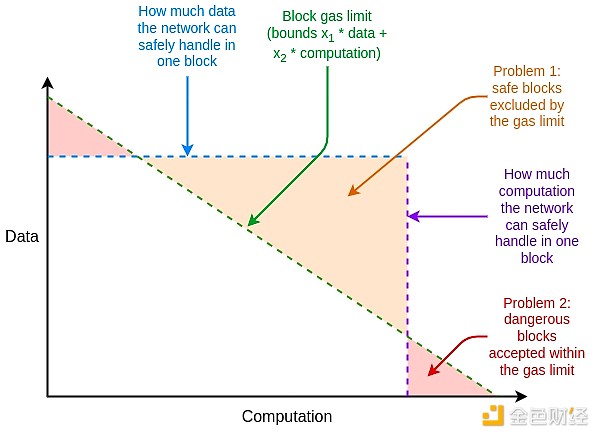
Multidimensional Gas allows the resource limits of a block to more closely replicate the resource limits of the underlying hardware.
Another “rabbit that popped out” was the proposal to delay state root computation until a slot after a block. This would give us a full 12 seconds to compute the state root, meaning that even in the most extreme case, only about 60,000 hashes/second of proving time would suffice, which again puts us in the realm of BLAKE3 being barely adequate.
The downside to this approach is that it adds a period of latency to light clients, although there are cleverer versions of the technique that could reduce this latency to just proof generation latency. For example, as soon as any node generates a proof, that proof could be broadcast on the network instead of waiting for the next block.
Solving the statelessness problem greatly increases the convenience of solo staking. This will become even more valuable if techniques that can lower the minimum balance for individual staking, such as Orbit SSF, or application-layer strategies such as squad staking, become available.
Multidimensional Gas becomes easier if EOF is introduced at the same time. This is because a key complexity of multidimensional Gas for execution is handling subcalls that do not pass the full Gas of the parent call, and EOF improves this by simply making such subcalls illegal (and the native account abstraction would provide an in-protocol alternative to the current primary use case for partial Gas subcalls).
Another important synergy is between stateless validation and history expiration. Today, clients have to store nearly a terabyte of history data; this amount of data is several times larger than the national data. Even if clients are stateless, the dream of almost storage-free clients is unattainable unless we also relieve clients of the responsibility of storing history. The first step in this regard is EIP-4444, which also means storing history in a torrent or portal network.
The long-term goal of Ethereum block validation is clear: you should be able to validate an Ethereum block by (i) downloading the block, or even perhaps just a small portion of it and sampling for data availability, and (ii) verifying that small portion proves that the block is valid. This would be a very cheap operation that could be done on a mobile client, in a browser wallet, or even (without the data availability part) in another chain.
To get to this point, you need to have SNARKs or STARKs for (i) the consensus layer (i.e. proof-of-stake) and (ii) the execution layer (i.e. the EVM). The former is a challenge in itself and should be addressed in the process of further improving the consensus layer (e.g., single-slot finality). The latter requires a proof of EVM execution.
Formally, in the Ethereum specification, the EVM is defined as a state transition function: you have some pre-state S, a block B, and you are computing a post-state S' = STF(S, B). If the user is using a light client, they don't have S and S', or even the full B; instead, they have a pre-state root R, a post-state root R', and a block hash H. The full statement that needs to be proved is approximately:
Public inputs: pre-state root R, post-state root R', block hash H.
Private inputs:Body of block B, objects in the state accessed by block Q, the same objects after executing block Q', a proof of state (e.g. a Merkle branch) P.
Claim 1:P is a valid proof that Q contains some portion of the state represented by R.
Claim 2:If you run STF on Q, (i) the execution only accesses objects inside Q, (ii) the block is valid, and (iii) the result is Q'.
Claim 3:If you recompute a new state root using the information in Q' and P, you will get R'.
If this exists, you can have a light client that can fully verify Ethereum EVM execution. This makes the client's resources already quite small. To get a truly fully validating Ethereum client, you also need to do the same for the consensus parties.
Implementations of validity proofs for EVM computations already exist and are heavily used by L2. However, there is still a lot of work to be done to make EVM validity proofs applicable to L1.
EC PSE ZK-EVM (now deprecated as better options exist): https://github.com/privacy-scaling-explorations/zkevm- Circuits
Zeth, which works by compiling the EVM into the RISC-0 ZK-VM: https://github.com/risc0/zeth
ZK-EVM Formal Verification Project: https://verified-zkevm.org/
Today, validity proofs for the EVM fall short in two areas: safety and proof time.
A secure validity proof requires ensuring that the SNARK actually verifies the EVM computation and that there are no bugs in it. The two main techniques for improving safety are multi-prover and formal verification. Multi-prover means having multiple independently written validity proof implementations, just like there are multiple clients, and having clients accept a block if a large enough subset of those implementations proves it. Formal verification involves using tools commonly used to prove mathematical theorems, such as Lean4, to prove that the validity proof only accepts input from a correct execution of the underlying EVM specification written in Python.
Fast enough proof time means that any Ethereum block can be proven in less than 4 seconds. Today, we are still far from this goal, although we are much closer than we thought two years ago. To achieve this we need to advance in three areas:
Parallelization — The fastest EVM prover today can prove an average Ethereum block in about 15 seconds. It does this by parallelizing across hundreds of GPUs and then aggregating their work together at the end. In theory, we know exactly how to make an EVM prover that can prove a computation in O(log(N)) time: have a GPU perform each step, and then perform the "aggregation tree":
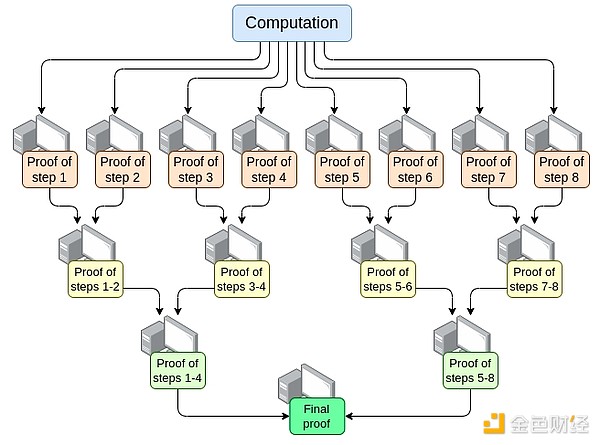
There are challenges in implementing this. To make it work even in the worst case (i.e. very large transactions taking up an entire block), the splitting of the computation cannot be per-transaction; it must be per-opcode (either the EVM or the underlying VM such as RISC-V). A key implementation challenge that makes this not entirely trivial is the need to ensure that the VM's "memory" is consistent between different parts of the proof. However, if we can do this kind of recursive proof, then we know that at least the prover latency problem is solved, even if there haven’t been any improvements on any other axis.
Proofing system optimizations — New proofing systems like Orion, Binius, GKR, etc. may lead to another big reduction in proving times for general purpose computation.
Other changes to EVM gas consumption — Many things in the EVM can be optimized to make it more prover friendly, especially in the worst case. Proving an average Ethereum block in 4 seconds isn’t enough if an attacker is able to construct a block that takes a prover ten minutes. The required EVM changes can be mainly divided into two categories:
Gas cost changes — If an operation takes a long time to prove, then it should have a high gas cost even if it is relatively fast to compute. EIP-7667 is a proposed EIP that deals with the worst issues in this regard: it significantly increases the gas cost of (legacy) hash functions that are relatively cheap opcodes and precompiles that are public. To compensate for these gas cost increases, we can reduce the gas cost of EVM opcodes that are relatively cheap to prove, thereby keeping the average throughput the same.
Data structure replacements — In addition to replacing the state trie with alternatives that are more suitable for STARKs, we also need to replace the transaction list, receipt trie, and other structures that are expensive to prove. Ethan Kissling’s EIP to move transaction and receipt structures to SSZ ([1] [2] [3]) is a step in this direction.
In addition to this, the two “rabbits out of the hat” mentioned in the previous section (multidimensional gas and delayed state roots) can also help here. However, it is worth noting that unlike stateless proof, which means we have enough technology to do what we need today, even with these technologies, full ZK-EVM proof will require more work — just less work.
One thing not mentioned above is proof hardware: using GPUs, FPGAs, and ASICs to generate proofs faster. Fabric Cryptography, Cysic, and Accseal are three companies driving this. This is very valuable for layer 2, but it is unlikely to be a decisive consideration for layer 1, because there is a strong desire to keep layer 1 highly decentralized, which means that proof generation must be within the capabilities of a significant subset of Ethereum users. Ethereum users should not be bottlenecked by the hardware of a single company. Layer 2 can make more aggressive tradeoffs.
There is more work to be done in these areas:
Parallel proofs require proof systems where different parts of a proof can "share memory" (e.g. a lookup table). We know techniques to do this, but they need implementation.
We need more analysis to figure out the ideal set of gas cost variations that minimize worst-case proof time.
We need more work on proof systems
Possible tradeoffs here include:
Security vs. prover time: Using aggressive choices of hash functions, proof systems with greater complexity or more aggressive security assumptions, or other design choices could potentially reduce prover time.
Decentralization & Prover Times:The community needs to agree on a “spec” for the prover hardware it is targeting. Is it okay to require provers to be large-scale entities? Do we want a high-end consumer laptop to be able to prove an Ethereum block in 4 seconds? Something in between?
Extent of breaking backwards compatibility:Deficiencies in other areas could be remedied by making more aggressive gas cost changes, but this is more likely to disproportionately increase costs for some applications and force developers to rewrite and redeploy code in order to remain economically viable. Likewise, the “rabbit in the hat” has its own complications and drawbacks.
The core technology required to implement EVM validity proofs on layer 1 is heavily shared with two other areas:
Validity proofs on layer 2 (i.e. “ZK rollups”)
The “STARK Binary Hash Proof” stateless approach
Successfully implementing validity proofs on layer 1 enables the ultimate in easy solo staking: even the weakest computers (including phones or smartwatches) will be able to stake. This further increases the value of solving other limitations on solo staking (e.g. the 32 ETH minimum).
In addition, EVM validity proofs on L1 can significantly increase L1’s gas limit.
The EVM execution isn't the only part we need to prove if we want to be able to fully verify Ethereum blocks with SNARKs. We also need to prove consensus: the part of the system that handles deposits, withdrawals, signatures, validator balance updates, and other elements of the Proof of Stake part of Ethereum.
Consensus is much simpler than the EVM, but the challenge with it is that we don't have a layer 2 EVM rollup, which is why most of the work has to be done anyway. Therefore, any implementation of proving Ethereum consensus needs to be done "from scratch", although the proving system itself is a shared work that can be built on top of it.
The beacon chain is defined as a state transition function, just like the EVM. The state transfer function is determined by three factors:
ECADD (used to verify BLS signatures)
Pairing (used to verify BLS signatures)
SHA256 hash (used to read and update state)
In each block, we need to attest 1-16 BLS12-381 ECADDs per validator (possibly more than one, as signatures can be included in multiple aggregates). This can be compensated for with subset precomputation techniques, so we can say that each validator is a BLS12-381 ECADD. Today, ~30,000 validators sign each epoch. In the future, this may change in either direction for single-slot finality (see explanation here): if we take the "brute force" route, it could increase to 1 million validators per slot. Meanwhile, with Orbit SSF it would remain at 32,768, or even decrease to 8,1.
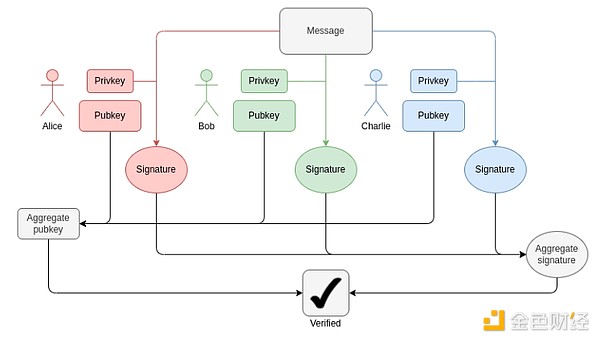
How BLS aggregation works. Verifying the aggregate signature only requires ECADD from each participant, not ECMUL. But 30,000 ECADDs is still a lot to prove.
For pairings, there is currently a maximum of 128 proofs per slot, which means 128 pairings need to be verified. With EIP-7549 and further changes, this could be reduced to 16 per slot. This is a small number of pairings, but extremely expensive: each pair takes thousands of times longer to run (or prove) than ECADD.
A major challenge in proving BLS12-381 operations is that there are no convenient curves with curve order equal to the BLS12-381 field size, which adds considerable overhead to any proving system. On the other hand, the Verkle trees proposed for Ethereum are built with Bandersnatch curves, which makes BLS12-381 itself a natural curve to use to prove Verkle branches in SNARK systems. A fairly simple implementation can provide about 100 G1 additions per second; clever techniques like GKR are almost certainly needed to prove fast enough.
For SHA256 hashes, the worst case scenario right now is an epoch transition block, where the entire validator short balanced tree and a large number of validator balances are updated. The validator short balanced tree is only one byte per validator, so about 1 MB of data is rehashed. This amounts to 32,768 SHA256 calls. If a thousand validators have balances above or below the threshold, the effective balances in the validator records need to be updated, which corresponds to a thousand Merkle branches, so potentially another ten thousand hashes. The shuffle mechanism requires 90 bits per validator (thus 11 MB of data), but this can be computed at any time during an epoch. For single-slot finality, these numbers may increase or decrease again depending on the details. Shuffling becomes unnecessary, although tracks may restore the need for shuffling to some extent.
Another challenge is the need to read all validator states (including public keys) to validate blocks. For 1 million validators, plus Merkle branches, reading the public keys alone requires 48 million bytes. This requires millions of hashes per epoch. If we had to prove proof-of-stake validation today, a realistic approach would be some form of incrementally verifiable computation: store a separate data structure in the proof system that is optimized for efficient lookups, and provide updates to this structure.
All in all, there are a lot of challenges.
Most effectively addressing these challenges will most likely require a deep redesign of the beacon chain, which could happen in parallel with the switch to single-slot finality. Features of this redesign could include:
Hash function changes:Today, the "full" SHA256 hash function is used, so each call corresponds to two underlying compression function calls due to padding. At a minimum, we can get a 2x gain by switching to the SHA256 compression function. If we use Poseidon instead, we can get a gain of about 100x, which completely solves all of our problems (at least for hashing): 1.7 million hashes per second (54 MB), and even "reading a million validator records" can be proven in seconds.
In the case of Orbit, store shuffled validator records directly:If you choose a certain number of validators (e.g. 8,192 or 32,768) to be the committee for a given slot, then put them directly into the state next to each other so that the minimum amount of hashes required to read all validator public keys into the proof. This will also allow all balance updates to be done efficiently.
Signature aggregation:Any high-performance signature aggregation scheme will actually involve some kind of recursive proof, where intermediate proofs of subsets of signatures will be made by various nodes in the network. This naturally spreads the proof load across many nodes in the network, making the "final prover" much less work.
Other signature schemes:For Lamport+Merkle signatures, we need 256+32 hashes to verify the signature; multiplied by 32,768 signers gives us 9,437,184 hashes. Optimizations to the signature scheme could improve this further by a small constant factor. If we use Poseidon, this is within the bounds of a single slot proof. But in practice, this gets much faster with a recursive aggregation scheme.
Succinct, Ethereum Proof of Consensus (Sync Committee only): https://github.com/succinctlabs/eth-proof-of-consensus
Succinct, Helios in SP1: https://github.com/succinctlabs/sp1-helios
Succinct BLS12-381 precompile: https://blog.succinct.xyz/succinctshipsprecompiles/
BLS aggregate signature verification based on Halo2: https://ethresear.ch/t/zkpos-with-halo2-pairing-for-verifying-aggregate-bls-signatures/14671
In reality, it will take us years to get proofs of validity for Ethereum consensus. This is roughly the same timeline as we need to achieve single-slot finality, rails, changes to the signing algorithm, and potential security analysis in order to have enough confidence to use a "radical" hash function like Poseidon. Therefore, it makes the most sense to solve these other problems, and keep STARK-friendliness in mind when doing this work.
The main tradeoff will most likely be in the order of operations, between a more gradual approach to reforming Ethereum's consensus layer and a more radical "many changes at once" approach. For the EVM, an incremental approach makes sense because it minimizes breaks to backwards compatibility. For the consensus layer, backwards compatibility issues are smaller, and there are benefits to a more "holistic" rethinking of the various details of how the beacon chain is built to best optimize for SNARK friendliness.
STARK friendliness needs to be a primary focus of the long-term redesign of Ethereum's proof-of-stake consensus, most notably single-slot finality, Orbit, changes to the signature scheme, and signature aggregation.
In efforts to increase security, banks in Singapore will soon be using Singpass face verification for customers setting up their digital tokens to prevent scams.
XingChiAt present, a few hundred GPU machines are enough to maintain the daily business of a ZK-based L2. So, what else should ZK accelerate, what is worth accelerating, and is the bottleneck of the ZK track in the generation or verification of proofs?
JinseFinanceAn important milestone in the Bitcoin ecosystem recently, Zulu announced the implementation of zk-SNARK verification (ZKP) using Bitcoin script.
JinseFinanceHow to verify ZK instructions? This article is fresh out of the box! In order to gain a deeper understanding of how formal verification techniques are applied to zkVM (zero-knowledge virtual machine), this article will focus on the verification of a single instruction.
JinseFinanceBitVM2 is a bold variant: anyone can serve as a validator.
JinseFinanceBlockchain and machine learning clearly have a lot in common: one is a technology that creates trust, and the other is a technology that desperately needs trust.
JinseFinanceThe UK government has confirmed its intention to regulate the cryptocurrency industry, with plans to introduce formal legislation by 2024. The announcement, part of the government's response to a consultation paper issued earlier this year, outlines the intention to bring various cryptoasset activities under the same regulations as banks and other financial services firms. The proposed regulations include stricter rules for exchanges, custodians, and crypto lending companies, with a focus on market abuse and cryptoasset issuance and disclosures. The UK aims to position itself as a global hub for cryptoasset technology through these regulatory measures.
BerniceThe newly tuned model has already introduced a new golden verification checkmark for businesses.
OthersA recent report hinted that a US federal court issued Celsius a formal summons.
OthersIt's not yet clear how the alleged criminal misconduct of a former employee led to a law enforcement freeze on user's funds.
Cointelegraph