Author: Haseeb Qureshi, Partner at Dragonfly Capital Source: medium Translation: Shan Ouba, Golden Finance
Suppose you want to run a large language model like Llama2–70B. Such a large model requires more than 140GB of memory, which means you can't run the original model on your home computer. What are your options? You might jump to a cloud provider, but you may not be too keen on trusting a single centralized company to handle this workload for you and collect all the usage data. Then what you need is decentralized inference, which allows you to run machine learning models without relying on any single provider.
Trust Problem
In a decentralized network, it is not enough to just run the model and trust the output. Suppose I ask the network to analyze the governance dilemma using Llama2-70B. How do I know it didn’t actually use Llama2–13B, give me a worse analysis, and pocket the difference?
In the centralized world, you might trust a company like OpenAI to do this honestly, because their reputation is at stake (and to some extent, the quality of LLM speaks for itself). But in the decentralized world, honesty isn’t assumed — it’s verified.
This is where verifiable inference comes into play. In addition to providing a response to a query, you can also prove that it ran correctly on the model you asked for. But how?
The simplest way is to run the model as an on-chain smart contract. This would certainly guarantee that the output is verified, but it’s highly impractical. GPT-3 represents words with an embedding dimension of 12,288. If you were to do a matrix multiplication of that size on-chain, it would cost about $10 billion at current gas prices — the computation would fill every block for about a month straight.
So no. We need a different approach.
After looking at the whole landscape, it’s clear to me that three main approaches have emerged to solve verifiable reasoning: zero-knowledge proofs, optimistic fraud proofs, and cryptoeconomics. Each has its own security and cost implications.
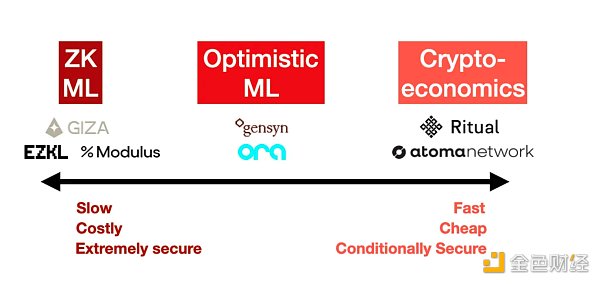
1. Zero-Knowledge Proofs (ZK ML)
Imagine being able to prove that you ran a large model, but that the proof is actually a fixed size no matter how large the model is. That’s what ZK ML promises through the magic of ZK-SNARKs.
While it sounds elegant in principle, compiling deep neural networks into zero-knowledge circuits and proving them is extremely difficult. It's also very costly - at a minimum, you might be looking at 1000x the cost of inference and 1000x the latency (the time to generate the proof), not to mention compiling the model itself into a circuit before any of this can happen. Ultimately, that cost has to be passed on to the user, so this ends up being very expensive for the end user.
On the other hand, this is the only way to guarantee correctness through cryptography. With ZK, the model provider can't cheat no matter how hard they try. But the cost of doing so is enormous, making it impractical for large models for the foreseeable future.
Examples: EZKL, Modulus Labs, Giza
2. Optimistic Fraud Proofs (Optimistic ML)
The optimistic approach is to trust, but verify. We assume that inferences are correct unless proven otherwise. If a node attempts to cheat, "observers" in the network can point out the cheater and challenge them with fraud proofs. These observers must always watch the chain and rerun the inference on their own models to ensure that the output is correct.
These fraud proofs are Truebit-style interactive challenge-response games where you repeatedly bisect the model execution trace on chain until you find the bug.
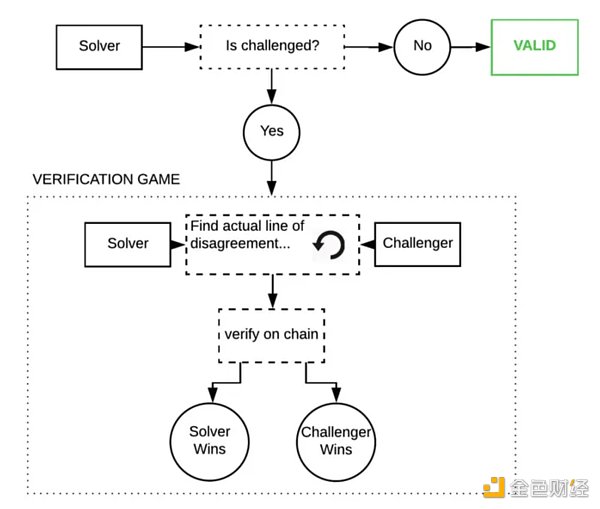
If this were to happen, it would be very expensive because these programs are so large and have huge internal states - a single GPT-3 inference costs about 1 petaflop (10^5 floating point operations). But game theory suggests this will almost never happen (fraud proofs are notoriously difficult to code correctly because the code is almost never attacked in production).
The optimistic benefit is that machine learning is safe as long as there is an honest observer watching. Cheaper than ZK ML, but remember that every observer in the network reruns every query on their own. In equilibrium, this means that if there are 10 observers, the security cost must be passed on to the users, so they will have to pay 10x more inference cost (or however many observers there are).
As with optimistic rollups, the downside is that you have to wait for the challenge period to pass before you can be sure the response has been validated. Depending on how the network is parameterized, though, you might have to wait minutes instead of days.
Examples: Ora, Gensyn (although unspecified at this time)
3. Cryptoeconomics (Cryptoeconomic ML)
Here we drop all the fancy tech and do something simple: stake-weighted voting. Users decide how many nodes should run their query, each node shows their response, and if there is a discrepancy between responses, the oddball node gets slashed. Standard oracle stuff - this is a more straightforward approach that lets users set the level of security they want, balancing cost and trust. If Chainlink were doing machine learning, they would do this.
The latency here is fast - you just need a commit-reveal from every node. If this is written into the blockchain, then technically this could happen in two blocks.
However, the security is at its weakest. A majority of nodes could rationally choose to collude if they are sufficiently crafty. As a user, you have to reason about how risky those nodes are and how much it would cost to cheat. That said, with things like Eigenlayer re-collateralization and attributable security, the network effectively provides insurance in the event of a security failure.
But the beauty of this system is that users can specify how secure they want to be. They can choose to include 3 nodes in the quorum, or 5 nodes, or every node in the network - or, if they want to YOLO, they can even choose n=1. The cost function here is simple: the user pays for the number of nodes they want in quorum. If they choose 3, they pay 3 times the inference cost.
Here comes the tricky question: can you make n=1 secure? In a simple implementation, if no one is checking, a single node should cheat every time. But I suspect that if you encrypt the query and send payments via intent, you might be able to confuse the node that they are actually the only one responding to this task. In this case, you might be able to charge the average user less than 2x the inference cost.
Ultimately, the cryptoeconomic approach is the simplest, easiest, and probably the cheapest, but it is the least sexy and, in principle, the least secure. But as always, the devil is in the details.
Examples: Ritual (although unspecified at this time), Atoma Network
Why Verifiable Machine Learning is Hard
You might be wondering why we don't have all this already? After all, at their core, machine learning models are just very large computer programs. Proving that programs executed correctly has long been the foundation of blockchains.
That’s why these three verification methods reflect the way blockchains secure their blockspace — ZK rollups use ZK proofs, optimistic rollups use fraud proofs, and most L1 blockchains use cryptoeconomics. Not surprisingly, we arrive at essentially the same solution. So what makes this hard when applied to machine learning?
ML is unique in that ML computations are typically represented as dense computation graphs designed to run efficiently on GPUs. They are not designed to be proven. So if you want to prove an ML computation in a ZK or optimistic setting, you have to recompile it in a format that makes that possible — which is very complex and expensive.
The second fundamental difficulty of machine learning is uncertainty. Program verification assumes that the output of the program is deterministic. But if you run the same model on different GPU architectures or CUDA versions, you will get different outputs. Even if you have to force each node to use the same architecture, you will still encounter problems with the randomness used in the algorithm (noise in the diffusion model, or token sampling in the LLM). You can fix the randomness by controlling the RNG seed. But even so, you still face the last threatening problem: the inherent uncertainty of floating-point operations.
Almost all operations in GPUs are done on floating-point numbers. Floating points are finicky because they are not associative — that is, (a + b) + c is not always the same as a + (b + c) for floating points. Since GPUs are highly parallelized, the order of additions or multiplications may be different each time they are executed, which can cause small differences in the output. This is unlikely to affect the output of an LLM given the discrete nature of words, but for an image model it could cause slightly different pixel values, resulting in two images not matching up perfectly.
This means that you either need to avoid using floating points, which means a huge hit to performance, or you need to allow some leniency when comparing outputs. Either way, the details are complex and you can’t completely abstract them away. (As it turns out, this is why the EVM doesn’t support floating point, even though some blockchains like NEAR do.)
In short, decentralized reasoning about networks is hard because all the details matter, and there are a staggering number of them.
Conclusion
At this point, it’s clear that blockchain and machine learning have a lot in common. One is a technology that creates trust, and the other is a technology that desperately needs trust. While each decentralized reasoning approach has its own tradeoffs, I’m very interested in learning how entrepreneurs use these tools to build the best possible networks.
 JinseFinance
JinseFinance







