Vitalik: Cách liên kết với Ethereum
"Liên kết Ethereum" bao gồm liên kết giá trị, liên kết công nghệ, liên kết kinh tế, v.v.
 JinseFinance
JinseFinance
Biên soạn bởi: Kate, Mars Finance
Trong hai năm qua, STARK đã trở thành chìa khóa và không thể thay thế công nghệ có thể tạo ra các bằng chứng mật mã có thể xác minh một cách hiệu quả cho các câu lệnh rất phức tạp (ví dụ: chứng minh rằng khối Ethereum là hợp lệ).
Một trong những lý do chính là kích thước trường: SNARK dựa trên đường cong elip yêu cầu bạn phải làm việc trên các số nguyên 256 bit để đủ an toàn; STARK cho phép bạn sử dụng các kích thước trường nhỏ hơn một cách hiệu quả hơn: các trường Goldilocks đầu tiên (số nguyên 64 bit), sau đó là Mersenne31 và BabyBear (cả hai đều 31 bit). Nhờ những lợi ích về hiệu quả này, Plonky2 sử dụng Goldilocks nhanh hơn hàng trăm lần so với các phiên bản tiền nhiệm trong việc chứng minh một loạt các phép tính.
Một câu hỏi tự nhiên là:Liệu chúng ta có thể đưa xu hướng này đi đến kết luận hợp lý hay không, xây dựng bằng cách vận hành trực tiếp trên các số 0 và 1. Các hệ thống bằng chứng chạy nhanh hơn
mạnh>? Đó chính xác là những gì Binius đang cố gắng thực hiện, sử dụng rất nhiều thủ thuật toán học khiến nó trở nên rất khác biệt so với SNARK và STARK ba năm trước. Bài viết này giải thích lý do tại sao các trường nhỏ giúp việc tạo bằng chứng hiệu quả hơn, tại sao trường nhị phân lại có sức mạnh đặc biệt và các thủ thuật mà Binius sử dụng để tạo ra bằng chứng trên trường nhị phân hiệu quả đến vậy.

△ Binius. Đến cuối bài viết này, bạn sẽ có thể hiểu từng phần của sơ đồ này.
Xem lại: trường hữu hạn
Mã hóa Một trong những chìa khóa Nhiệm vụ của hệ thống chứng minh là xử lý một lượng lớn dữ liệu trong khi vẫn giữ số lượng nhỏ. Nếu bạn có thể cô đọng một phát biểu về một chương trình lớn thành một phương trình toán học chứa một vài con số, nhưng những con số đó lớn bằng chương trình ban đầu thì bạn sẽ chẳng đi đến đâu cả.
Để thực hiện các phép tính phức tạp trong khi vẫn giữ các số nhỏ, các nhà mật mã học thường sử dụng số học mô-đun. Chúng tôi chọn số nguyên tố "modulo" p. Toán tử % có nghĩa là "lấy phần còn lại": 15%7=1, 53%10=3, v.v. (Lưu ý rằng câu trả lời luôn không phủ định, vì vậy, ví dụ -1%10=9)

Bạn có thể đã thấy số học mô-đun trong bối cảnh cộng và trừ thời gian (ví dụ: 4 giờ sau đó là mấy giờ 9 giờ? Nhưng ở đây, chúng ta không chỉ cộng và trừ mô đun của một số nhất định mà còn có thể nhân, chia và lấy số mũ
Chúng tôi định nghĩa lại:
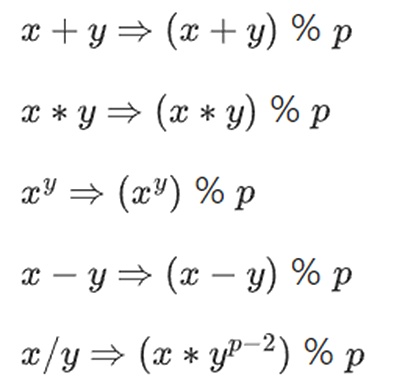
Các quy tắc trên là tự đồng nhất. Ví dụ: nếu p=7 thì:
5+3=1 (vì 8% 7=1)
1-3=5 (vì -2%7=5)
2*5=3
3/5=2
Một thuật ngữ tổng quát hơn đối với cấu trúc này là một trường hữu hạn là một cấu trúc toán học tuân theo các định luật số học thông thường nhưng có số lượng giá trị có thể hạn chế để mỗi giá trị có thể được biểu diễn bằng một kích thước cố định kiểu
SNARK và STARK Cách chứng minh một chương trình máy tính là thông qua số học: bạn thực hiện một phép Chuyển đổi phát biểu của chương trình mà bạn muốn chứng minh thành một phương trình toán học chứa đa thức. Giải pháp hiệu quả cho các phương trình tương ứng với việc thực hiện hiệu quả chương trình.
Như một ví dụ đơn giản, giả sử tôi tính số Fibonacci thứ 100 và tôi muốn chứng minh cho bạn thấy nó là gì. Tôi đã tạo một đa thức F mã hóa dãy Fibonacci: vậy F(0)=F(1)=1, F(2)=2, F(3)=3, F(4)=5, v.v., tổng cộng trong số 100 bước. Điều kiện mình cần chứng minh là F(x+2)=F(x)+F(x+1) trong toàn dãy x={0,1…98}. Tôi có thể thuyết phục bạn bằng cách đưa ra thương số:
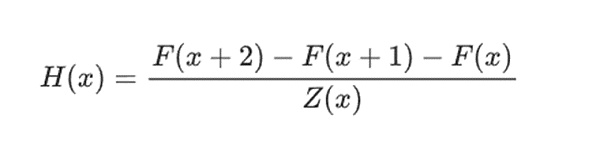
Trong đó Z(x) = (x-0) * (x-1) * …(x-98). .Nếu tôi có thể cung cấp rằng có F và H thỏa mãn phương trình này thì F phải thỏa mãn F(x+2)-F(x+1)-F(x) trong phạm vi đó. Nếu tôi xác minh thêm rằng F thỏa mãn, F(0)=F(1)=1, thì F(100) thực sự phải là số Fibonacci thứ 100.
Nếu bạn muốn chứng minh điều gì đó phức tạp hơn, thì bạn thay thế quan hệ "đơn giản" F(x+2) = F(x ) + F(x+ 1), về cơ bản có nội dung "F(x+1) là đầu ra của quá trình khởi tạo máy ảo có trạng thái F(x)" và chạy một bước tính toán. Bạn cũng có thể thay thế số 100 bằng số lớn hơn, ví dụ: 100000000, để phù hợp với nhiều bước hơn.
Tất cả SNARK và STARK đều dựa trên ý tưởng sử dụng các phương trình đơn giản trên đa thức (và đôi khi là vectơ và ma trận) để thể hiện mối quan hệ lớn giữa các giá trị đơn lẻ . Không phải tất cả các thuật toán đều kiểm tra tính tương đương giữa các bước tính toán liền kề như trên: ví dụ PLONK không, R1CS cũng không. Tuy nhiên, nhiều hoạt động kiểm tra hiệu quả nhất thực hiện việc này vì thực hiện cùng một hoạt động kiểm tra (hoặc cùng một số hoạt động kiểm tra) nhiều lần sẽ giúp giảm thiểu chi phí dễ dàng hơn.
Plonky2: Từ SNARK 256-bit và STARK đến 64-bit...chỉ STARK
Năm năm trước, một bản tóm tắt hợp lý về các loại bằng chứng không có kiến thức khác nhau như sau. Có hai loại bằng chứng: SNARK (dựa trên đường cong elip) và STARK (dựa trên hàm băm). Về mặt kỹ thuật, STARK là một loại SNARK, nhưng trong thực tế, "SNARK" thường được dùng để chỉ biến thể dựa trên đường cong elip, trong khi "STARK" được dùng để chỉ cấu trúc dựa trên hàm băm. SNARK có kích thước nhỏ nên bạn có thể xác minh chúng rất nhanh và cài đặt chúng vào chuỗi một cách dễ dàng. STARK có kích thước lớn nhưng không yêu cầu thiết lập đáng tin cậy và có khả năng chống lượng tử.

△ STARK hoạt động bằng cách xử lý dữ liệu dưới dạng đa thức, tính toán tính toán của đa thức đó và sử dụng gốc Merkle của dữ liệu mở rộng như một "cam kết đa thức".
Một lịch sử quan trọng ở đây là SNARK dựa trên đường cong elip lần đầu tiên được sử dụng rộng rãi: phải đến khoảng năm 2018, STARK mới trở nên đủ hiệu quả, điều này đòi hỏi phải có Nhờ FRI, Zcash đã hoạt động được hơn một năm vào thời điểm đó. SNARK dựa trên đường cong elip có một hạn chế chính: nếu bạn muốn sử dụng SNARK dựa trên đường cong elip thì phép tính trong các phương trình này phải được thực hiện bằng cách sử dụng mô đun điểm trên đường cong elip. Đây là một số lớn, thường gần bằng 2, lũy thừa 256: ví dụ: đường cong bn128 là 21888242871839275222246405745257275088548364400416034343698204186575808495617. Nhưng các phép tính thực tế sử dụng những con số nhỏ: nếu bạn nghĩ về một chương trình "thực" bằng ngôn ngữ yêu thích của bạn, hầu hết những thứ nó sử dụng là bộ đếm, chỉ mục trong vòng lặp for, vị trí trong chương trình, đại diện cho Đúng hoặc Một bit Sai và những thứ khác hầu như luôn chỉ dài một vài chữ số.
Ngay cả khi dữ liệu "gốc" của bạn bao gồm các số "nhỏ", quá trình chứng minh yêu cầu tính toán thương số, khai triển, kết hợp tuyến tính ngẫu nhiên và các phép biến đổi dữ liệu khác, mà sẽ dẫn đến số lượng đối tượng bằng hoặc nhiều hơn có kích thước trung bình lớn bằng kích thước đầy đủ của trường của bạn. Điều này tạo ra sự kém hiệu quả quan trọng: để chứng minh một phép tính trên n giá trị nhỏ, bạn phải thực hiện nhiều phép tính nữa trên n giá trị lớn hơn nhiều. Ban đầu, STARK kế thừa thói quen sử dụng trường 256-bit của SNARK và do đó cũng gặp phải tình trạng thiếu hiệu quả tương tự.

△ Một số phần mở rộng của Reed-Solomon cho đánh giá đa thức. Mặc dù giá trị ban đầu nhỏ nhưng các giá trị bổ sung sẽ được mở rộng đến kích thước đầy đủ của trường (trong trường hợp này là 2 lũy thừa 31 - 1)
2022 Năm 2016, Plonky2 được phát hành. Sự đổi mới chính của Plonky2 là modulo số học một số nguyên tố nhỏ hơn: 2 lũy thừa 64 – 2 lũy thừa 32 + 1 = 18446744067414584321. Giờ đây, mỗi phép cộng hoặc phép nhân luôn có thể được thực hiện bằng một vài lệnh trên CPU và việc băm tất cả dữ liệu lại với nhau nhanh hơn gấp 4 lần so với trước đây. Nhưng có một vấn đề: cách tiếp cận này chỉ hiệu quả với STARK. Nếu bạn cố gắng sử dụng SNARK, các đường cong elip sẽ trở nên không an toàn đối với các đường cong elip nhỏ như vậy.
Để đảm bảo an ninh, Plonky2 cũng cần giới thiệu các trường mở rộng. Một kỹ thuật quan trọng để kiểm tra các phương trình số học là "lấy mẫu điểm ngẫu nhiên": nếu bạn muốn kiểm tra xem H(x) * Z(x) có bằng F(x+2)-F(x+1)-F(x) hay không , bạn Bạn có thể chọn ngẫu nhiên tọa độ r, cung cấp bằng chứng cam kết đa thức để chứng minh H(r), Z(r), F(r), F(r+1) và F(r+2), sau đó xác minh H( r) * Z(r) có bằng F(r+2)-F(r+1)- F(r). Nếu kẻ tấn công có thể đoán trước tọa độ thì kẻ tấn công có thể đánh lừa hệ thống chứng minh - đây là lý do tại sao hệ thống chứng minh phải là ngẫu nhiên. Nhưng điều này cũng có nghĩa là tọa độ phải được lấy mẫu từ một tập đủ lớn để kẻ tấn công không thể đoán ngẫu nhiên. Điều này rõ ràng đúng nếu mô đun gần bằng 2 được nâng lên lũy thừa thứ 256. Nhưng đối với đại lượng modulo bằng 2 lũy thừa 64 -2 lũy thừa 32 +1, chúng ta vẫn chưa đạt đến mức đó, và điều đó chắc chắn không xảy ra nếu chúng ta giảm xuống 2 lũy thừa 31 -1. Cố gắng giả mạo bằng chứng 2 tỷ lần cho đến khi một người gặp may chắc chắn nằm trong khả năng của kẻ tấn công.
Để tránh điều này, chúng tôi lấy mẫu r từ trường mở rộng. Ví dụ: bạn có thể xác định y trong đó y được nâng lên lũy thừa ba = 5 và lấy 1 , y. , sự kết hợp của y với lũy thừa của 2. Điều này sẽ tăng tổng số tọa độ lên khoảng 2 mũ 93. Hầu hết các đa thức mà người chứng minh tính toán không nằm trong miền mở rộng này; chúng chỉ là số nguyên modulo 2 lũy thừa 31 -1, vì vậy bạn vẫn nhận được tất cả hiệu quả từ việc sử dụng một miền nhỏ. Tuy nhiên, việc kiểm tra điểm ngẫu nhiên và tính toán FRI thực sự đi sâu vào lĩnh vực rộng lớn hơn này để có được mức độ bảo mật mà bạn cần.
Từ số nguyên tố nhỏ đến số nhị phân
Máy tính so sánh Các số lớn được biểu diễn dưới dạng chuỗi 0 và 1 để thực hiện các phép tính số học và các "mạch" được xây dựng trên các bit này để tính toán các phép tính như cộng và nhân. Máy tính được tối ưu hóa đặc biệt cho số nguyên 16 bit, 32 bit và 64 bit. Ví dụ: 2 lũy thừa 64 - 2 lũy thừa 32 + 1 và 2 lũy thừa 31 - 1 được chọn không chỉ vì chúng phù hợp với các giới hạn này mà còn vì chúng rất phù hợp với các giới hạn này: bạn có thể làm điều này bằng cách thực hiện Phép nhân 32 bit thông thường để thực hiện phép nhân modulo 2 64 - 2 32 + 1, đồng thời dịch chuyển từng bit và sao chép kết quả đầu ra ở một số vị trí; bài viết này giải thích rõ một số kỹ thuật.
Tuy nhiên, cách tiếp cận tốt hơn là thực hiện các phép tính trực tiếp dưới dạng nhị phân. Điều gì sẽ xảy ra nếu phép cộng có thể "chỉ" là một XOR mà không phải lo lắng về việc "mang" tràn khi thêm 1 + 1 từ bit này sang bit tiếp theo? Điều gì sẽ xảy ra nếu phép nhân có thể được song song hơn theo cách tương tự? Những ưu điểm này dựa trên việc có thể sử dụng một bit để biểu thị giá trị đúng/sai.
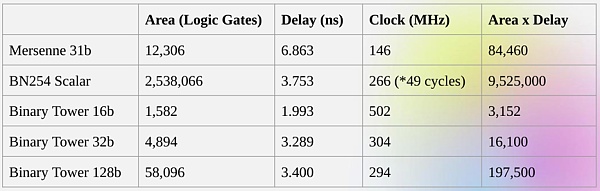
Có được những lợi ích này của việc thực hiện trực tiếp các phép tính nhị phân chính xác là những gì Binius cố gắng thực hiện. Nhóm Binius đã chứng minh sự cải thiện hiệu quả trong bài phát biểu của họ tại zkSummit:
 p>
p>
Mặc dù "kích thước" gần giống nhau, nhưng các phép toán trường nhị phân 32-bit yêu cầu tài nguyên máy tính ít hơn 5 lần so với các phép toán trường Mersenne 31-bit.
Từ đa thức đến siêu khối
Giả sử chúng ta tin vào Lý do này và muốn làm mọi thứ với bit (0 và 1). Làm cách nào để biểu diễn một tỷ bit bằng đa thức?
Ở đây, chúng ta gặp phải hai vấn đề thực tế:
Để một đa thức biểu thị một số lượng lớn các giá trị, các giá trị này cần phải được truy cập trong quá trình đánh giá đa thức: trong ví dụ Fibonacci ở trên, F(0), F(1) … F (100), và trong phép tính lớn hơn, số mũ lên tới hàng triệu. Các trường chúng tôi sử dụng cần chứa các số có kích thước tối đa này.
Chứng minh rằng mọi giá trị chúng tôi gửi trong cây Merkle (giống như tất cả STARK) là bắt buộc Solomon mã hóa nó: ví dụ: mở rộng giá trị từ n lên 8n, sử dụng tính dư thừa để ngăn chặn kẻ gian lận bằng cách giả mạo một giá trị trong quá trình tính toán. Điều này cũng yêu cầu một trường đủ lớn: để mở rộng từ một triệu giá trị lên 8 triệu, bạn cần 8 triệu điểm khác nhau để đánh giá đa thức.
Ý tưởng chính của Binius là giải quyết hai vấn đề này một cách riêng biệt và biểu diễn cùng một dữ liệu theo hai cách khác nhau để đáp ứng . Đầu tiên, chính đa thức.
Các hệ thống như SNARK dựa trên đường cong elip, STARK thời 2019, Plonky2, v.v. thường xử lý các đa thức có một biến: F(x). Mặt khác, Binius lấy cảm hứng từ giao thức Spartan và sử dụng đa thức đa biến: F(x1,x2,… xk). Trên thực tế, chúng ta biểu diễn toàn bộ quỹ đạo tính toán trên một "siêu khối" tính toán trong đó mọi xi đều là 0 hoặc 1. Ví dụ: nếu muốn biểu thị một chuỗi Fibonacci và vẫn sử dụng trường đủ lớn để biểu thị chúng, chúng ta có thể nghĩ về 16 chuỗi đầu tiên của chúng như thế này:

Nói cách khác, F(0 ,0,0, 0) phải là 1, F(1,0,0,0) cũng là 1, F(0,1,0,0) là 2, v.v., cho đến khi F(1,1,1 ,1)=987 . Với một siêu khối của các phép tính như vậy, có một đa thức tuyến tính đa biến (độ 1 cho mỗi biến) tạo ra các phép tính này. Vì vậy, chúng ta có thể coi tập hợp các giá trị này là biểu diễn của đa thức; chúng ta không cần tính các hệ số.
Ví dụ này tất nhiên chỉ để minh họa: trong thực tế, toàn bộ mục đích của việc đi vào một siêu khối là để chúng ta xử lý các bit riêng lẻ. Cách "Binius gốc" để tính số Fibonacci là sử dụng khối lập phương có chiều cao hơn, sử dụng mỗi nhóm, ví dụ: 16 bit để lưu trữ một số. Cần một chút khéo léo để thực hiện phép cộng số nguyên trên cơ sở bit, nhưng đối với Binius thì điều đó không quá khó.
Bây giờ, chúng ta hãy xem các mã xóa. Cách STARK hoạt động là: bạn lấy n giá trị, Reed-Solomon mở rộng chúng thành nhiều giá trị hơn (thường là 8n, thường là từ 2n đến 32n), sau đó chọn ngẫu nhiên một số nhánh Merkle từ bản mở rộng và thực hiện một số loại kiểm tra trên chúng. Chiều dài của hypercube là 2 ở mỗi chiều. Do đó, việc mở rộng nó một cách trực tiếp là không thực tế: không có đủ "khoảng trống" để lấy mẫu nhánh Merkle từ 16 giá trị. Vậy ta phải làm sao? Giả sử hypercube là một hình vuông!
Binius đơn giản - một ví dụ
Giới thiệu về giao thức dành cho quá trình triển khai python, vui lòng sao chép liên kết bên dưới vào trình duyệt của bạn để xem: https://github.com/ethereum/research/blob/master/binius/simple_binius.py
Hãy xem một ví dụ, sử dụng số nguyên thông thường làm trường để thuận tiện (trong triển khai thực tế, các phần tử trường nhị phân sẽ được sử dụng). Đầu tiên, chúng tôi mã hóa siêu khối mà chúng tôi muốn gửi dưới dạng hình vuông:
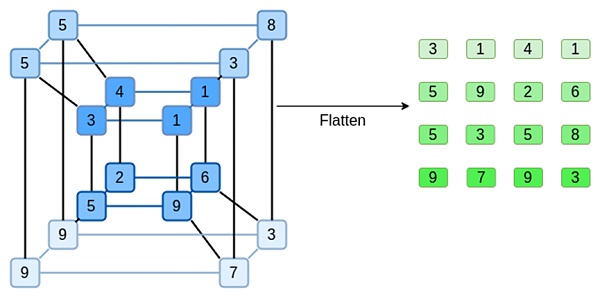
Bây giờ, chúng ta mở rộng hình vuông bằng Reed-Solomon. Nghĩa là, chúng ta coi mỗi hàng là đa thức bậc 3 được đánh giá tại x = {0,1,2,3} và đánh giá cùng đa thức đó tại x = {4,5,6,7}:

Hãy cẩn thận, con số có thể tăng lên nhanh chóng! Đó là lý do tại sao trong triển khai thực tế, chúng tôi luôn sử dụng các trường hữu hạn, không phải số nguyên thông thường: ví dụ: nếu chúng tôi sử dụng số nguyên modulo 11, thì phần mở rộng của dòng đầu tiên sẽ chỉ là [3,10,0,6].
Nếu bạn muốn thử tiện ích mở rộng và tự mình xác minh các con số tại đây, bạn có thể sử dụng mã tiện ích mở rộng Reed-Solomon đơn giản của tôi tại đây.
Tiếp theo, chúng tôi coi phần mở rộng này là một cột và tạo cây Merkle của cột. Rễ của cây Merkel là những cam kết của chúng ta.
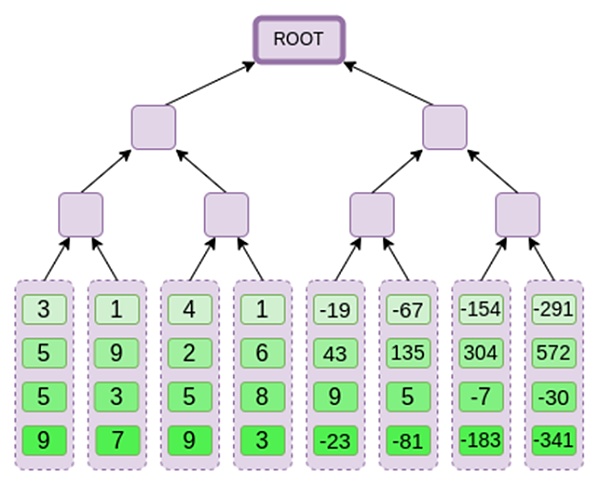
Bây giờ, giả sử rằng người chứng minh muốn chứng minh tính toán của đa thức r={r0,r1,r2,r3} này tại một thời điểm nào đó. Có một sự khác biệt nhỏ trong Binius khiến nó yếu hơn so với các sơ đồ cam kết đa thức khác: người chứng minh không được biết hoặc không thể đoán s trước khi xác nhận các gốc Merkle (nói cách khác, r phải là một giá trị giả ngẫu nhiên). Điều này làm cho lược đồ trở nên vô dụng đối với việc "tra cứu cơ sở dữ liệu" (ví dụ: "Được rồi, bạn đã đưa cho tôi gốc Merkle, bây giờ hãy chứng minh cho tôi P(0,0,1,0)!").
Nhưng các giao thức chứng minh không có kiến thức mà chúng tôi thực sự sử dụng thường không yêu cầu "tra cứu cơ sở dữ liệu"; chúng chỉ cần kiểm tra đa thức tại một điểm đánh giá ngẫu nhiên. Vì vậy, hạn chế này phục vụ mục đích của chúng tôi.
Giả sử chúng ta chọn r={1,2,3,4} (Kết quả tính toán đa thức là -137 tại thời điểm này; bạn có thể sử dụng mã này để xác nhận ) . Bây giờ chúng ta bước vào quá trình chứng minh. Chúng ta chia r thành hai phần: phần đầu tiên {1,2} biểu thị tổ hợp tuyến tính của các cột trong một hàng và phần thứ hai {3,4} biểu thị tổ hợp tuyến tính của các hàng. Chúng tôi tính toán "tích tensor" cho phần cột:
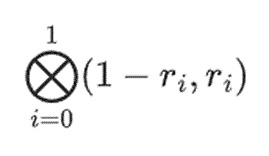 < /p>
< /p>
Đối với phần dòng:

Điều này có nghĩa là: danh sách tất cả các sản phẩm có thể có với một giá trị trong mỗi bộ. Trong trường hợp hàng, chúng tôi nhận được:
[(1-r2)*(1-r3), (1-r3), (1-r2)* r3 , r2*r3]
Sử dụng r={1,2,3,4} (vì vậy r2=3 và r3=4):
< p style="text-align: left;">[(1-3)*(1-4), 3*(1-4),(1-3)*4,3*4] = [6, - 9 -8 -12]Bây giờ, chúng ta tính toán một "hàng" t mới bằng cách lấy tổ hợp tuyến tính của các hàng hiện có. Nói cách khác, chúng tôi lấy:
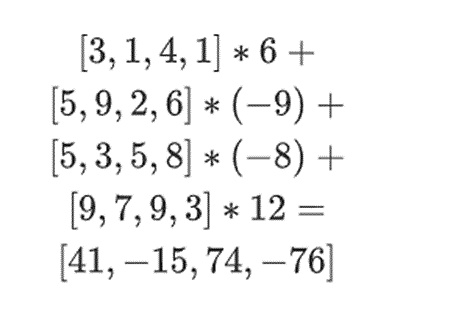
Bạn có thể coi những gì đang xảy ra ở đây là sự đánh giá một phần. Nếu chúng ta nhân tích tensor đầy đủ với vectơ đầy đủ của tất cả các giá trị, bạn sẽ nhận được phép tính P(1,2,3,4) = -137. Ở đây, chúng tôi nhân tích tensor một phần chỉ bằng một nửa tọa độ được đánh giá và giảm lưới giá trị N thành một hàng giá trị N gốc. Nếu bạn đưa dòng này cho người khác, họ có thể thực hiện phần còn lại của phép tính bằng cách sử dụng tích tensor của nửa tọa độ được đánh giá còn lại.
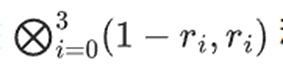
Người chứng minh cung cấp cho người xác minh bằng chứng Merkle của hàng mới sau: t và một số cột được lấy mẫu ngẫu nhiên. Trong ví dụ minh họa của chúng tôi, chúng tôi sẽ yêu cầu người hoạt ngôn chỉ cung cấp cột cuối cùng; trong thực tế, người hoạt ngôn sẽ cần cung cấp hàng tá cột để đạt được mức độ bảo mật đầy đủ.
Bây giờ, chúng ta tận dụng tính tuyến tính của mã Reed-Solomon. Thuộc tính chính mà chúng tôi sử dụng là: lấy tổ hợp tuyến tính của khai triển Reed-Solomon cho kết quả tương tự như khai triển Reed-Solomon của tổ hợp tuyến tính. Sự "độc lập về trật tự" này thường xảy ra khi cả hai phép toán đều tuyến tính.
Người xác minh thực hiện chính xác việc này. Họ tính toán các kết hợp t và tuyến tính của cùng các cột mà người chứng minh đã tính toán trước đó (nhưng chỉ các cột do người chứng minh cung cấp) và xác minh rằng cả hai quy trình đều đưa ra cùng một câu trả lời.
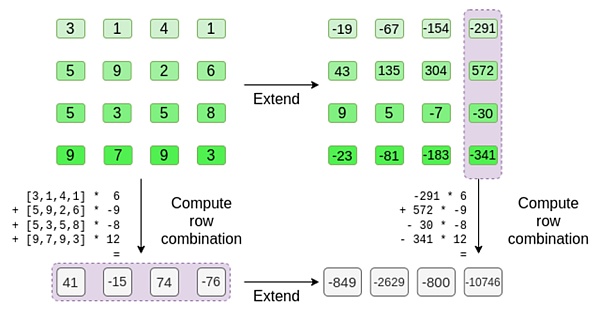
Trong trường hợp này, khai triển t, tính tổ hợp tuyến tính giống nhau ([6,-9,-8,12], cả hai đều cho cùng một đáp án: -10746. Điều này chứng tỏ cội nguồn của Merkel được xây dựng với "ý định tốt" ( hoặc ít nhất là "đủ gần") và nó khớp với t: ít nhất phần lớn các cột tương thích với nhau
Nhưng còn một cách xác thực nữa. điều mà người xác minh cần kiểm tra: kiểm tra việc đánh giá đa thức {r0…r3} cho đến nay, không có bước nào của người xác minh thực sự phụ thuộc vào các giá trị được người chứng minh xác nhận. Đây là những gì chúng tôi kiểm tra sản phẩm Tensor được đánh dấu là "cột. phần" của điểm tính toán:
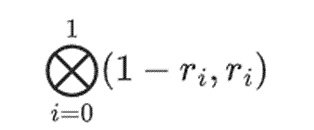
Trong ví dụ của chúng tôi, trong đó r={1,2,3,4} nên một nửa cột được chọn là {1,2}), giá trị này Bằng:
< p style="text-align:center">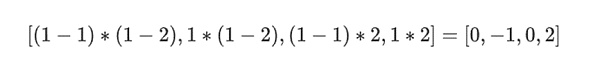
Bây giờ chúng ta lấy sự kết hợp tuyến tính này t:
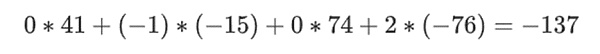 < /p>
< /p>
Điều này giống như kết quả của việc giải trực tiếp đa thức.
Phần trên rất gần với mô tả đầy đủ về giao thức Binius "đơn giản". Điều này đã có một số lợi thế thú vị: ví dụ: vì dữ liệu được chia thành hàng và cột nên bạn chỉ cần một trường có kích thước bằng một nửa. Tuy nhiên, điều này không nhận ra đầy đủ lợi ích của việc tính toán ở dạng nhị phân. Để làm được điều này, chúng ta cần giao thức Binius đầy đủ. Nhưng trước tiên, chúng ta hãy xem xét sâu hơn về trường nhị phân.
Trường nhị phân
Miền nhỏ nhất có thể là số học mô-đun 2. Nó rất nhỏ, chúng ta có thể viết các bảng cộng và nhân của nó:
Chúng ta có thể nhận được các trường nhị phân lớn hơn bằng cách mở rộng: nếu chúng ta bắt đầu từ F2 (số nguyên modulo 2) thì hãy xác định x trong đó x bình phương = x +1, chúng ta nhận được các bảng cộng và nhân sau:
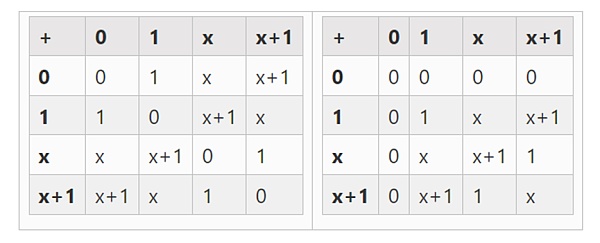
Hóa ra là chúng ta có thể chia tỷ lệ trường nhị phân thành kích thước lớn tùy ý bằng cách lặp lại cấu trúc này. Không giống như số phức trên số thực, trong đó bạn có thể thêm một phần tử mới, nhưng không thể thêm bất kỳ phần tử I nào nữa (các phần tư có tồn tại, nhưng chúng kỳ lạ về mặt toán học, ví dụ: ab không bằng ba), hãy sử dụng các trường hữu hạn, bạn luôn có thể thêm mới phần mở rộng. Cụ thể, định nghĩa của chúng tôi về các phần tử như sau:
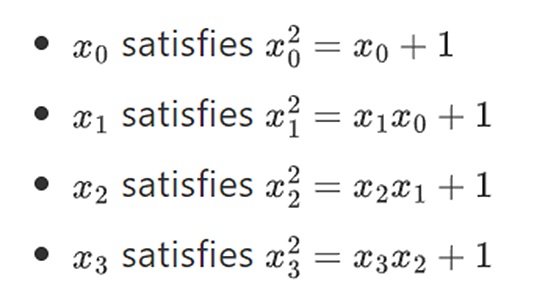
Đợi đã... Điều này thường được gọi là cấu trúc tháp vì mỗi lần mở rộng liên tiếp có thể được coi là thêm một lớp mới vào tháp. Đây không phải là cách duy nhất để xây dựng các trường nhị phân có kích thước tùy ý, nhưng nó có một số lợi thế độc đáo mà Binius tận dụng.
Chúng ta có thể biểu diễn những số này dưới dạng danh sách các bit. Ví dụ: 1100101010001111. Bit đầu tiên biểu thị bội số của 1, bit thứ hai biểu thị bội số của x0, sau đó các bit tiếp theo biểu thị bội số của các số x1 sau: x1, x1*x0, x2, x2*x0, v.v. Mã hóa này rất hay vì bạn có thể chia nhỏ nó:
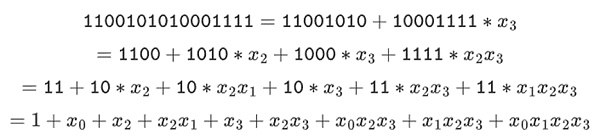
Đây là một ký hiệu tương đối hiếm gặp, nhưng tôi thích biểu diễn các phần tử trường nhị phân dưới dạng số nguyên, sử dụng cách biểu diễn bit hiệu quả hơn với các bit ở bên phải. Nghĩa là, 1=1, x0=01=2, 1+x0=11=3, 1+x0+x2=11001000 =19, v.v. Trong biểu thức này, nó là 61779.
Phép cộng trong trường nhị phân chỉ là XOR (nhân tiện, cũng như phép trừ); lưu ý rằng điều này có nghĩa là x+x=0 với mọi x. Để nhân hai phần tử x*y, có một thuật toán đệ quy rất đơn giản: chia mỗi số làm đôi:

Sau đó, chia phép nhân:
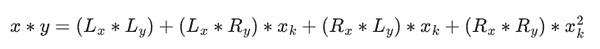
Phần cuối cùng là phần duy nhất hơi phức tạp một chút vì bạn phải Đăng ký quy tắc đơn giản hóa Có nhiều cách hiệu quả hơn để thực hiện phép nhân, tương tự như thuật toán của Karatsuba và Biến đổi Fourier nhanh, nhưng tôi sẽ coi đó là bài tập để người đọc quan tâm tìm ra.
Việc chia trong trường nhị phân được thực hiện bằng cách kết hợp phép nhân và phép đảo ngược. Phương pháp đảo ngược “đơn giản nhưng chậm” là một ứng dụng của định lý nhỏ Fermat tổng quát. Ngoài ra còn có thuật toán đảo ngược phức tạp hơn nhưng hiệu quả hơn mà bạn có thể tìm thấy ở đây. Bạn có thể sử dụng mã ở đây để chơi với phép cộng, nhân và chia các trường nhị phân.
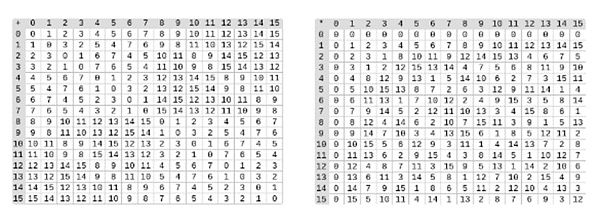
△ Bên trái: Bảng cộng các phần tử trường nhị phân 4 chữ số (tức là chỉ 1, x0, x1, x0x1). Bên phải: Bảng nhân cho các phần tử trường nhị phân bốn chữ số.
Cái hay của loại trường nhị phân này là nó kết hợp một số phần hay nhất của số nguyên "thông thường" và số học mô-đun. Giống như các số nguyên thông thường, các phần tử trường nhị phân không bị giới hạn: bạn có thể mở rộng chúng theo ý muốn. Nhưng cũng giống như số học modulo, nếu bạn thao tác trên các giá trị trong một giới hạn kích thước nhất định, tất cả kết quả của bạn cũng sẽ nằm trong cùng một phạm vi. Ví dụ: nếu bạn lấy 42 lũy thừa liên tiếp, bạn sẽ nhận được:
 < /p >
< /p >
Sau 255 bước, bạn quay lại 42 lũy thừa 255 = 1. Cũng giống như số nguyên dương và số học môđun, chúng tuân theo các định luật toán học thông thường: a *b= b*a, a*(b+c)=a*b+a*c và thậm chí một số luật mới kỳ lạ.
Cuối cùng, các trường nhị phân giúp bạn dễ dàng xử lý các bit: nếu bạn làm toán với các số vừa 2 được nâng lên lũy thừa thứ k thì tất cả đầu ra của bạn cũng sẽ khớp 2 đến bit nguồn thứ k. Điều này tránh được sự bối rối. Trong EIP-4844 của Ethereum, mỗi "khối" của blob phải là một mô-đun kỹ thuật số 52435875175126190479447740508185965837690552500527637822603658699938581184513, do đó, việc mã hóa dữ liệu nhị phân yêu cầu loại bỏ một số khoảng trống và thực hiện kiểm tra A bổ sung để đảm bảo rằng mỗi khối phần tử lưu trữ giá trị nhỏ hơn 2 mũ 248 .
Điều này cũng có nghĩa là các thao tác trường nhị phân cực kỳ nhanh trên máy tính - cả CPU lẫn các thiết kế FPGA và ASIC tối ưu về mặt lý thuyết.
Điều này có nghĩa là chúng ta có thể làm những gì chúng ta đã làm với mã hóa Reed-Solomon ở trên, theo cách hoàn toàn tránh được "sự bùng nổ" của số nguyên, giống như những gì chúng ta đã thấy trong ví dụ của mình, và theo một cách rất "bản địa", là kiểu tính toán mà máy tính rất giỏi. Thuộc tính "phân chia" của các trường nhị phân - cách chúng tôi thực hiện 1100101010001111=11001010+10001111*x3 và sau đó phân chia nó theo nhu cầu của chúng tôi cũng rất quan trọng để đạt được nhiều tính linh hoạt.
Hoàn thành Binius
Vui lòng triển khai giao thức Python sao chép liên kết bên dưới vào trình duyệt của bạn để xem: https://github.com/ethereum/research/blob/master/binius/packed_binius.py
Bây giờ, chúng ta có thể chuyển sang "Full Binius", điều chỉnh "Simple Binius" để (i) hoạt động trên các trường nhị phân và (ii) cho phép chúng ta chuyển giao một bit. Giao thức này khó hiểu vì nó chuyển đổi qua lại giữa các cách khác nhau để xem ma trận bit; tất nhiên tôi phải mất nhiều thời gian hơn để hiểu nó so với thông thường để hiểu các giao thức mã hóa. Nhưng một khi bạn hiểu được các trường nhị phân, tin tốt là "toán học khó hơn" mà Binius dựa vào không tồn tại.
Đây không phải là ghép nối đường cong elip, nơi có các lỗ thỏ hình học đại số ngày càng sâu hơn để khoan ở đây, bạn chỉ cần các trường nhị phân.
Hãy xem lại biểu đồ đầy đủ:

Bây giờ, bạn đã quen thuộc với hầu hết các thành phần. Ý tưởng "làm phẳng" hypercube thành một lưới, ý tưởng tính toán kết hợp hàng và kết hợp cột dưới dạng tích tensor của các điểm đánh giá và thử nghiệm "Mở rộng Reed-Solomon rồi tính toán kết hợp hàng" và "tính toán kết hợp hàng và sau đó là Reed- Ý tưởng về sự tương đương giữa các phần mở rộng của Solomon được triển khai trong Binius đơn giản.
Có gì mới trong "Complete Binius"? Về cơ bản có ba điều:
Các giá trị riêng lẻ trong siêu khối và hình vuông phải là bit( 0 hoặc 1).
Quá trình mở rộng mở rộng các bit thành nhiều hơn bằng cách nhóm chúng thành các cột và tạm thời giả định rằng chúng là các phần tử trường lớn hơn.
Sau bước tập hợp hàng, có một bước "phân tách thành bit" theo phần tử để chuyển phần mở rộng trở lại thành bit.
Chúng ta sẽ lần lượt thảo luận về hai tình huống này. Đầu tiên, quá trình mở rộng mới. Mã Reed-Solomon có một hạn chế cơ bản, nếu bạn muốn mở rộng n thành k*n, bạn cần phải làm việc trong các trường có k*n giá trị khác nhau có thể được sử dụng làm tọa độ. Bạn không thể làm điều đó với F2 (hay còn gọi là bit). Vì vậy, điều chúng ta làm là "đóng gói" các phần tử của F2 liền kề lại với nhau để tạo thành một giá trị lớn hơn. Trong ví dụ ở đây, chúng tôi gói hai bit cùng một lúc vào các phần tử {0, 1, 2, 3}, điều này là đủ đối với chúng tôi vì tiện ích mở rộng của chúng tôi chỉ có bốn điểm tính toán. Trong bằng chứng "thực", chúng ta có thể trả về 16 bit mỗi lần. Sau đó, chúng tôi thực thi mã Reed-Solomon trên các giá trị được đóng gói này và giải nén chúng thành từng bit một lần nữa.

Bây giờ, kết hợp hàng. Để thực hiện kiểm tra "đánh giá tại điểm ngẫu nhiên" một cách an toàn bằng mật mã, chúng ta cần lấy mẫu điểm từ một không gian khá lớn (lớn hơn nhiều so với chính siêu khối). Vì vậy, trong khi các điểm bên trong hypercube là bit thì các giá trị được tính toán bên ngoài hypercube sẽ lớn hơn rất nhiều. Trong ví dụ trên, "tổ hợp hàng" có kết quả là [11,4,6,1].
Điều này đặt ra một vấn đề: chúng ta biết cách kết hợp các bit thành một giá trị lớn hơn và sau đó thực hiện khai triển Reed-Solomon trên cơ sở này, nhưng còn việc thực hiện thì sao? điều tương tự cho các cặp giá trị lớn hơn?
Bí quyết của Binius là làm việc trên cơ sở bit: chúng ta xem xét từng bit của mỗi giá trị (ví dụ: đối với thứ gì đó chúng ta gắn nhãn "11", nghĩa là [1, 1,0,1] ) và sau đó mở rộng theo hàng. Thực hiện quá trình mở rộng trên đối tượng. Nghĩa là, chúng tôi thực hiện quá trình mở rộng trên 1 hàng của mỗi phần tử, sau đó trên hàng x0, sau đó trên hàng "x1", rồi trên hàng x0x1, v.v. (à, trong ví dụ về đồ chơi của chúng tôi, Chúng tôi đã dừng ở đó, nhưng trong triển khai thực tế, chúng tôi sẽ đạt tới 128 dòng (dòng cuối cùng là x6*…*x0 ))
Review
Xem lại
strong>Chúng tôi chuyển đổi các bit trong siêu khối thành một lưới, sau đó chúng tôi coi các nhóm bit liền kề trên mỗi hàng là các phần tử trường lớn hơn và thực hiện các phép toán số học trên chúng để Reed-Solomon mở rộng các hàng.
Tiếp theo, chúng tôi lấy tổ hợp hàng của các bit cho mỗi cột và lấy cột bit cho mỗi hàng làm đầu ra (nhỏ hơn nhiều đối với các hình vuông lớn hơn 4x4).
Cuối cùng, chúng tôi coi kết quả đầu ra là một ma trận và các bit của nó là các hàng.
Tại sao lại thế này? Trong toán học "thông thường", nếu bạn bắt đầu chia một số thành các bit, khả năng (thường) thực hiện các phép tính tuyến tính theo bất kỳ thứ tự nào và nhận được kết quả tương tự sẽ bị hỏng.
Ví dụ: nếu tôi bắt đầu với số 345 và nhân nó với 8 rồi nhân với 3, tôi nhận được 8280. Nếu tôi đảo ngược hai phép tính này, tôi cũng nhận được 8280. Nhưng nếu tôi chèn thao tác "chia theo bit" giữa hai bước, nó sẽ gặp sự cố: nếu bạn thực hiện 8x, rồi 3x, bạn sẽ nhận được:
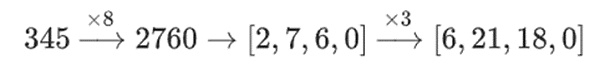
Nhưng nếu bạn làm 3 lần thì hãy làm 8 lần và bạn sẽ nhận được :
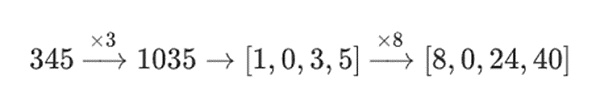
Nhưng trong trường nhị phân được xây dựng bằng cấu trúc tháp, cách tiếp cận này có hiệu quả. Lý do nằm ở khả năng phân tách của chúng: nếu bạn nhân một giá trị lớn với một giá trị nhỏ thì những gì xảy ra trên mỗi phân đoạn vẫn ở trên mỗi phân đoạn. Nếu chúng ta nhân 1100101010001111 với 11 thì kết quả này giống với phân tách đầu tiên của 1100101010001111, đó là

Sau đó nhân mỗi thành phần với 11 cho cùng.
Đặt chúng lại với nhau
Nói chung, Không có kiến thức Hệ thống chứng minh hoạt động bằng cách đưa ra các phát biểu về đa thức đồng thời biểu diễn các phát biểu về đánh giá cơ bản: như chúng ta đã thấy trong ví dụ Fibonacci, F(X+2)-F(X+1) -F(X) = Z(X)*H (X) kiểm tra đồng thời tất cả các bước tính toán Fibonacci. Chúng ta kiểm tra các phát biểu về đa thức bằng cách chứng minh đánh giá tại các điểm ngẫu nhiên. Việc kiểm tra các điểm ngẫu nhiên này thể hiện việc kiểm tra toàn bộ đa thức: nếu một phương trình đa thức không khớp, có một khả năng nhỏ là nó sẽ khớp ở một tọa độ ngẫu nhiên cụ thể.
Trong thực tế, một trong những lý do chính dẫn đến sự kém hiệu quả là trong các chương trình thực, hầu hết các con số chúng ta xử lý đều nhỏ: các chỉ mục trong vòng lặp for, True / Giá trị sai, bộ đếm và những thứ tương tự. Tuy nhiên, khi chúng tôi sử dụng mã hóa Reed-Solomon để "mở rộng" dữ liệu nhằm cung cấp độ dư thừa cần thiết để đảm bảo an toàn cho việc kiểm tra dựa trên bằng chứng Merkle, hầu hết các giá trị "phụ" cuối cùng sẽ chiếm toàn bộ kích thước của trường, thậm chí nếu giá trị ban đầu nhỏ.
Để giải quyết vấn đề này, chúng tôi muốn làm cho trường này càng nhỏ càng tốt. Plonky2 đưa chúng ta từ số 256 bit xuống số 64 bit, sau đó Plonky3 giảm tiếp xuống số 31 bit. Nhưng ngay cả điều này cũng không tối ưu. Sử dụng các trường nhị phân, chúng ta có thể xử lý một bit. Điều này làm cho mã hóa "dày đặc": nếu dữ liệu cơ bản thực tế của bạn có n bit thì mã hóa của bạn sẽ là n bit và phần mở rộng sẽ là 8 * n bit, không có chi phí bổ sung.
Bây giờ, hãy nhìn vào biểu đồ lần thứ ba:

Trong Binius, chúng tôi làm việc trên đa thức đa tuyến tính: siêu khối P(x0, x1,… xk), trong đó một đánh giá duy nhất P(0,0,0,0), P(0,0,0,1) cho đến P(1,1,1,1), sẽ lưu dữ liệu mà chúng ta quan tâm. Để minh họa phép tính tại một điểm nhất định, chúng tôi "diễn giải lại" dữ liệu tương tự dưới dạng hình vuông. Sau đó, chúng tôi mở rộng từng hàng bằng cách sử dụng mã hóa Reed-Solomon để cung cấp khả năng dự phòng dữ liệu cần thiết nhằm bảo mật cho các truy vấn nhánh Merkle ngẫu nhiên. Sau đó, chúng tôi tính toán các kết hợp tuyến tính ngẫu nhiên của các hàng, thiết kế các hệ số sao cho các hàng kết hợp mới thực sự chứa các giá trị được tính toán mà chúng tôi quan tâm. Hàng mới được tạo này (được diễn giải lại dưới dạng bit 128 hàng) và một số cột được chọn ngẫu nhiên có nhánh Merkle được chuyển đến trình xác minh.
Sau đó, trình xác nhận thực hiện "mở rộng các kết hợp hàng" (hay chính xác hơn là mở rộng một số cột) và "mở rộng các kết hợp hàng", và Xác minh rằng hai kết quả khớp nhau. Sau đó tính toán tổ hợp cột và kiểm tra xem nó có trả về giá trị được người chứng minh khẳng định hay không. Đây là hệ thống chứng minh của chúng tôi (hay đúng hơn là sơ đồ cam kết đa thức, là thành phần chính của hệ thống chứng minh).
Chúng ta chưa đề cập đến điều gì?
Thuật toán hiệu quả để mở rộng hàng, thuật toán này thực sự được cải thiện trong tính toán của trình xác nhận. cho hiệu quả. Chúng tôi sử dụng Biến đổi Fourier nhanh trên các trường nhị phân, được mô tả ở đây (mặc dù cách triển khai chính xác sẽ khác nhau, vì bài viết này sử dụng cấu trúc kém hiệu quả hơn không dựa trên việc mở rộng đệ quy).
Số học. Đa thức một biến rất tiện lợi vì bạn có thể thực hiện những việc như F(X+2)-F(X+1)-F(X) = Z(X)*H(X) để liên hệ các bước liền kề trong phép tính. Trong hypercube, "bước tiếp theo" khó hiểu hơn nhiều so với "X+1". Bạn có thể thực hiện X+k, lũy thừa của k, nhưng hành vi nhảy này sẽ làm mất đi nhiều ưu điểm chính của Binius. Giải pháp được trình bày trong bài báo Binius. (Xem Phần 4.3), nhưng bản thân đây đã là một cái hố sâu.
Cách thực hiện kiểm tra giá trị cụ thể một cách an toàn. Ví dụ về Fibonacci yêu cầu kiểm tra các điều kiện biên chính: F(0)=F(1)=1 và giá trị của F(100). Nhưng với Binius "thô", việc kiểm tra tại các điểm tính toán đã biết là không an toàn. Có một số cách khá đơn giản để chuyển một phép tính đã biết thành một phép tính chưa xác định, bằng cách sử dụng cái gọi là giao thức kiểm tra tổng; nhưng chúng tôi sẽ không đề cập đến những cách đó ở đây.
Giao thức tra cứu, một kỹ thuật khác được sử dụng rộng rãi gần đây, được sử dụng để Tạo một kết quả siêu hiệu quả hệ thống chứng minh. Binius có thể được sử dụng cùng với nhiều giao thức tra cứu ứng dụng.
Vượt quá thời gian xác minh căn bậc hai. Căn bậc hai rất đắt: Bằng chứng Binius của Bit từ 2 lũy thừa 32 dài khoảng 11MB. Bạn có thể bù đắp cho vấn đề này bằng cách sử dụng các hệ thống chứng minh khác để tạo ra "bằng chứng về bằng chứng Binius", nhờ đó đạt được hiệu quả của bằng chứng Binius và kích thước bằng chứng nhỏ hơn. Một tùy chọn khác là giao thức FRI-binius phức tạp hơn, tạo ra bằng chứng có kích thước đa logarit (giống như FRI thông thường).
Binius ảnh hưởng như thế nào đến "sự thân thiện với SNARK". Tóm tắt cơ bản là nếu bạn sử dụng Binius, bạn không còn phải lo lắng về việc thực hiện phép tính "thân thiện với số học": băm "thông thường" không còn hiệu quả hơn băm số học truyền thống, nhân modulo 2 lũy thừa 32 hoặc modulo 2 256 không còn là vấn đề đau đầu so với mô đun nhân, v.v. Nhưng đây là một chủ đề phức tạp. Rất nhiều thứ thay đổi khi mọi thứ được thực hiện ở dạng nhị phân.
Tôi hy vọng sẽ có nhiều cải tiến hơn đối với kỹ thuật chứng minh dựa trên trường nhị phân trong những tháng tới.
"Liên kết Ethereum" bao gồm liên kết giá trị, liên kết công nghệ, liên kết kinh tế, v.v.
 JinseFinance
JinseFinanceĐiều kiện tiên quyết để hiểu được bài viết này là bạn đã hiểu được nguyên tắc cơ bản của SNARK và STARK. Nếu bạn không quen với điều này, tôi khuyên bạn nên đọc một số phần đầu tiên của bài viết này để hiểu những điều cơ bản.
 JinseFinance
JinseFinanceETH, cách giải thích bài viết mới nhất của Vitalik Golden Finance, linh hồn của Ethereum và bản chất của thế giới tiền điện tử nằm ở đó.
 JinseFinance
JinseFinanceVitalik đã hợp tác với bốn đồng tác giả để công bố trong một bài nghiên cứu giới thiệu một điều kỳ diệu về công nghệ được gọi là "nhóm quyền riêng tư", được thiết kế để giải quyết một trong những vấn đề cấp bách nhất trong lĩnh vực blockchain.
 Catherine
CatherineBản cập nhật mới bao gồm “The Scourge” sẽ giúp giải quyết các vấn đề về MEV.
 Beincrypto
BeincryptoThật là một thập kỷ của các bài tiểu luận - bao gồm mọi thứ từ mã thông báo Soulbound đến DAO siêu lý trí - nói về Ethereum và tiền điện tử.
 Coindesk
CoindeskNhà phát minh Ethereum Vitalik Buterin và cha của ông là Dmitry “Dima” Buterin đã nói về thị trường tiền điện tử, sự biến động và các nhà đầu cơ. ...
 Bitcoinist
BitcoinistSo với PoW, PoS là một cơ chế bảo mật chuỗi khối tốt hơn.
 链向资讯
链向资讯So với PoW, PoS là một cơ chế bảo mật chuỗi khối tốt hơn.
 Ftftx
FtftxQuốc gia nhỏ bé ở Đông Nam châu Âu đang bắt đầu sàng lọc qua vùng nước âm u của quy định blockchain bằng cách cấp quyền công dân cho người đồng sáng lập Ethereum.
 Cointelegraph
Cointelegraph