فيتاليك: كيفية التوافق مع إيثريوم
تتضمن "محاذاة الإيثيريوم" توافق القيمة، ومواءمة التكنولوجيا، والمواءمة الاقتصادية، وما إلى ذلك.
 JinseFinance
JinseFinance
تم إعداده بواسطة: Kate, Mars Finance
على مدى العامين الماضيين، أصبح STARK مفتاحًا ولا يمكن الاستغناء عنه التكنولوجيا التي يمكن أن تنتج بكفاءة أدلة تشفير يمكن التحقق منها بسهولة لبيانات معقدة للغاية (على سبيل المثال، إثبات أن كتلة إيثريوم صالحة).
أحد الأسباب الرئيسية هو حجم الحقل: تتطلب SNARKs المستندة إلى المنحنى الإهليلجي العمل على أعداد صحيحة 256 بت أن يكون آمنًا بدرجة كافية؛ ويتيح لك STARK استخدام أحجام حقول أصغر بشكل أكثر كفاءة: أولاً حقول Goldilocks (أعداد صحيحة 64 بت)، ثم Mersenne31 وBabyBear (كلاهما 31 بت). وبسبب هذه المكاسب في الكفاءة، فإن استخدام Plonky2 لـ Goldilocks أسرع بمئات المرات من سابقاتها في إثبات مجموعة واسعة من الحسابات.
السؤال الطبيعي هو:هل يمكننا أن نأخذ هذا الاتجاه إلى نهايته المنطقية، من خلال البناء مباشرة على أنظمة إثبات الأصفار والآحاد التي تعمل بشكل أسرع
قوي>؟ وهذا بالضبط ما يحاول Binius فعله، مستخدمًا الكثير من الحيل الرياضية التي تجعله مختلفًا تمامًا عن SNARK وSTARK منذ ثلاث سنوات. تشرح هذه المقالة لماذا تجعل الحقول الصغيرة إنشاء البراهين أكثر كفاءة، ولماذا تكون الحقول الثنائية قوية بشكل فريد، والحيل التي يستخدمها Binius لعمل البراهين على الحقول الثنائية فعالة للغاية.
△ بينيوس. بحلول نهاية هذه المقالة، يجب أن تكون قادرا على فهم كل جزء من هذا المخطط.
مراجعة: الحقول المحدودة
التشفير أحد المفاتيح تتمثل مهام نظام الإثبات في العمل على كميات كبيرة من البيانات مع الحفاظ على الأرقام صغيرة. إذا تمكنت من اختصار عبارة حول برنامج كبير في معادلة رياضية تحتوي على بضعة أرقام، ولكن هذه الأرقام كبيرة مثل البرنامج الأصلي، فلن تصل إلى أي مكان.
لإجراء عمليات حسابية معقدة مع إبقاء الأرقام صغيرة، غالبًا ما يستخدم علماء التشفير الحساب المعياري. نختار رقمًا أوليًا "modulo" p. عامل التشغيل % يعني "أخذ الباقي": 15%7=1، 53%10=3، إلخ. (لاحظ أن الإجابة دائمًا غير سلبية، فمثلاً -1%10=9)

ربما تكون قد شاهدت الحساب المعياري في سياق جمع وطرح الوقت (على سبيل المثال، ما هو الوقت بعد 4 ساعات) الساعة 9؟ لكن هنا، لا نقوم فقط بجمع وطرح معامل رقم معين، بل يمكننا أيضًا الضرب والقسمة وأخذ الأس
نعيد تعريف:
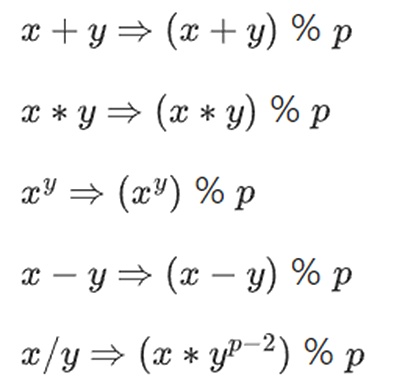
القواعد المذكورة أعلاه متسقة ذاتيًا. على سبيل المثال، إذا كانت p=7، إذن:
5+3=1 (لأن 8% 7=1)
1-3=5 (لأن -2%7=5)
2*5=3
3/5=2
مصطلح أكثر عمومية لأن هذا الهيكل عبارة عن حقل محدود والمجال المحدود هو هيكل رياضي يتبع القوانين الحسابية المعتادة ولكن له عدد محدود من القيم الممكنة بحيث يمكن تمثيل كل قيمة بحجم ثابت
الحساب المعياري (أو حقول الأعداد الأولية) هو النوع الأكثر شيوعًا للحقول المحدودة، ولكن هناك أيضًا نوع آخر: الحقول الموسعة، ربما تكون قد شاهدت حقلاً ممتدًا: الأعداد المركبة. تخيل" عنصرًا جديدًا وقم بتعيينه بتسمية i وإجراء العمليات الحسابية معه: (3i+2)*(2i+4)=6i*i+12i+4i+8=16i+2. يمكننا بالمثل أن نأخذ امتداد يصبح توسيع الحقول الأولية ذا أهمية متزايدة لحماية الأمان حيث تصبح الحقول أصغر، في حين تعتمد الحقول الثنائية (التي يستخدمها Binius) بشكل كامل على التوسع للحصول على أي فائدة عملية : left;">مراجعة: الحساب
SNARK وSTARK الطريقة لإثبات برنامج كمبيوتر هي من خلال الحساب: تأخذ تحويلاً بيان البرنامج الذي تريد إثباته في معادلة رياضية تحتوي على كثيرة الحدود. تتوافق الحلول الفعالة للمعادلات مع التنفيذ الفعال للبرنامج.
كمثال بسيط، لنفترض أنني قمت بحساب رقم فيبوناتشي رقم 100 وأريد أن أثبت لك ما هو. لقد قمت بإنشاء كثيرة الحدود F التي تشفر تسلسل فيبوناتشي: لذا F(0)=F(1)=1، F(2)=2، F(3)=3، F(4)=5 وهكذا، المجموع من 100 خطوة. الشرط الذي أحتاج إلى إثباته هو أن F(x+2)=F(x)+F(x+1) في النطاق بأكمله x={0,1…98}. يمكنني إقناعك بإعطائك الناتج:
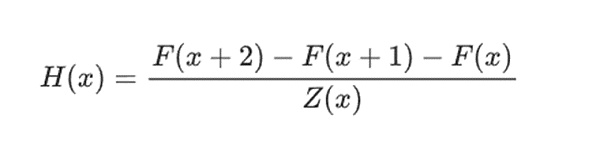
حيث Z(x) = (x-0) * (x-1) * …(x-98). إذا كان بإمكاني توفير أن هناك F وأن H يفي بهذه المعادلة، فيجب أن تحقق F F(x+2)-F(x+1)-F(x) في هذا النطاق. إذا قمت أيضًا بالتحقق من استيفاء F، F(0)=F(1)=1، فيجب أن يكون F(100) هو رقم فيبوناتشي رقم 100.
إذا كنت تريد إثبات شيء أكثر تعقيدًا، فاستبدل العلاقة "البسيطة" F(x+2) = F(x ) + F(x+ 1)، والذي ينص بشكل أساسي على أن "F(x+1) هو ناتج تهيئة جهاز افتراضي بالحالة F(x)" ويقوم بتشغيل خطوة حسابية. يمكنك أيضًا استبدال الرقم 100 برقم أكبر، مثلاً 100000000، لاستيعاب المزيد من الخطوات.
تعتمد جميع SNARKs وSTARKs على فكرة استخدام معادلات بسيطة على كثيرات الحدود (وأحيانًا المتجهات والمصفوفات) لتمثيل العلاقات الكبيرة بين القيم الفردية. لا تتحقق جميع الخوارزميات من التكافؤ بين الخطوات الحسابية المتجاورة على النحو الوارد أعلاه: على سبيل المثال، لا تقوم PLONK بذلك، ولا R1CS. لكن العديد من عمليات الفحص الأكثر كفاءة تفعل ذلك لأن إجراء نفس الفحص (أو نفس عمليات التحقق القليلة) عدة مرات يجعل من السهل تقليل النفقات العامة.
Plonky2: من SNARK وSTARK 256 بت إلى 64 بت...فقط STARK
قبل خمس سنوات، كان الملخص المعقول للأنواع المختلفة من إثباتات المعرفة الصفرية على النحو التالي. هناك نوعان من البراهين: (المعتمد على المنحنى الناقص) SNARK و (المعتمد على التجزئة) STARK. من الناحية الفنية، STARK هو نوع من SNARK، ولكن من الناحية العملية، غالبًا ما يتم استخدام "SNARK" للإشارة إلى المتغير القائم على المنحنى الإهليلجي، بينما يتم استخدام "STARK" للإشارة إلى البنية القائمة على التجزئة. SNARKs صغيرة الحجم، لذا يمكنك التحقق منها بسرعة كبيرة وتثبيتها على السلسلة بسهولة. STARKs كبيرة الحجم، لكنها لا تتطلب إعدادًا موثوقًا به، كما أنها مقاومة للكم.

△ يعمل STARK من خلال التعامل مع البيانات باعتبارها كثيرة الحدود، وحساب حساب كثير الحدود، واستخدام جذر Merkle للبيانات الموسعة باعتباره "التزامًا متعدد الحدود".
التاريخ الرئيسي هنا هو أن SNARKs القائم على المنحنى الإهليلجي أصبح يستخدم على نطاق واسع لأول مرة: ولم يصبح STARKs فعالاً بدرجة كافية إلا في عام 2018 تقريبًا، الأمر الذي تطلب الشكر FRI، كان Zcash يعمل لأكثر من عام في ذلك الوقت. SNARKs المستندة إلى المنحنى الإهليلجي لها قيود رئيسية: إذا كنت تريد استخدام SNARKs المستندة إلى المنحنى الإهليلجي، فيجب إجراء العمليات الحسابية في هذه المعادلات باستخدام معامل النقطة على المنحنى الإهليلجي. هذا رقم كبير، عادة ما يكون قريبًا من 2 مرفوعًا للأس 256: على سبيل المثال، منحنى bn128 هو 21888242871839275222246405745257275088548364400416034343698204186575808495617. لكن الحسابات الفعلية تستخدم أرقامًا صغيرة: إذا كنت تفكر في برنامج "حقيقي" بلغتك المفضلة، فإن معظم الأشياء التي يستخدمها هي العدادات، والفهارس في الحلقات، والمواضع في البرنامج، والتي تمثل صحيحًا أو جزءًا واحدًا من الخطأ ، وغيرها من الأشياء التي تتكون دائمًا من بضعة أرقام فقط.
حتى لو كانت بياناتك "الأصلية" تتكون من أرقام "صغيرة"، فإن عملية الإثبات تتطلب حساب خارج القسمة والتوسعات والمجموعات الخطية العشوائية وتحويلات البيانات الأخرى، والتي سيؤدي إلى عدد مساوٍ أو أكبر من الكائنات التي يكون متوسط حجمها كبيرًا مثل الحجم الكامل لحقلك. وهذا يخلق عدم كفاءة رئيسية: من أجل إثبات عملية حسابية على قيم n صغيرة، عليك إجراء العديد من العمليات الحسابية على قيم n أكبر بكثير. في البداية، ورثت STARK عادة SNARK المتمثلة في استخدام حقول 256 بت، وبالتالي عانت من نفس أوجه القصور.

△ بعض امتدادات ريد-سولومون لتقييم كثيرات الحدود. على الرغم من أن القيمة الأصلية صغيرة، إلا أنه سيتم توسيع القيم الإضافية إلى الحجم الكامل للحقل (في هذه الحالة 2 أس 31 - 1)
2022 في عام 2016، تم إصدار Plonky2. الابتكار الرئيسي في Plonky2 هو المعامل الحسابي لعدد أولي أصغر: 2 أس 64 - 2 أس 32 + 1 = 18446744067414584321. الآن، يمكن دائمًا إجراء كل عملية إضافة أو ضرب في بعض التعليمات على وحدة المعالجة المركزية، كما أصبح تجزئة جميع البيانات معًا أسرع 4 مرات من ذي قبل. ولكن هناك مشكلة: هذا النهج يعمل فقط مع ستارك. إذا حاولت استخدام SNARKs، تصبح المنحنيات الإهليلجية غير آمنة لمثل هذه المنحنيات الإهليلجية الصغيرة.
لضمان الأمان، يحتاج Plonky2 أيضًا إلى تقديم حقول موسعة. الأسلوب الرئيسي للتحقق من المعادلات الحسابية هو "أخذ عينات من النقاط العشوائية": إذا كنت تريد التحقق مما إذا كانت H(x) * Z(x) تساوي F(x+2)-F(x+1)-F(x) ، يمكنك تحديد إحداثي r بشكل عشوائي، وتقديم دليل التزام متعدد الحدود لإثبات H(r)، وZ(r)، وF(r)، وF(r+1) وF(r+2)، ثم التحقق من H( ص) * هل Z(r) يساوي F(r+2)-F(r+1)- F(r). إذا تمكن المهاجم من تخمين الإحداثيات مسبقًا، فيمكنه خداع نظام الإثبات - ولهذا السبب يجب أن يكون نظام الإثبات عشوائيًا. ولكن هذا يعني أيضًا أنه يجب أخذ عينات من الإحداثيات من مجموعة كبيرة بما يكفي بحيث لا يستطيع المهاجم تخمينها بشكل عشوائي. ومن الواضح أن هذا صحيح إذا كان المعامل قريبًا من 2 مرفوعًا للقوة 256. لكن بالنسبة لكمية معيارية 2 أس 64 -2 أس 32 +1، لم نصل إلى هذه المرحلة بعد، وبالتأكيد ليس هذا هو الحال إذا نزلنا إلى 2 أس 31 -1. إن محاولة تزييف الدليل 2 مليار مرة حتى يحالفك الحظ هو بالتأكيد ضمن قدرات المهاجم.
لمنع ذلك، قمنا باختبار r من الحقل الممتد. على سبيل المثال، يمكنك تعريف y حيث y مرفوع للقوة الثالثة = 5 وأخذ 1 , y ، الجمع بين y للقوة 2. سيؤدي هذا إلى زيادة إجمالي عدد الإحداثيات إلى حوالي 2 أس 93. معظم كثيرات الحدود التي يحسبها المثل لا تدخل في هذا المجال الموسع؛ فهي مجرد أعداد صحيحة من 2 أس 31 -1، لذلك لا تزال تحصل على كل الكفاءة من استخدام مجال صغير. لكن التحقق العشوائي من النقاط وحسابات FRI يتعمق حقًا في هذا المجال الأكبر للحصول على الأمان الذي تحتاجه.
من الأعداد الأولية الصغيرة إلى الأعداد الثنائية
الكمبيوتر يتم تمثيل الأعداد الكبيرة على شكل تسلسلات من 0 و1 لإجراء العمليات الحسابية، ويتم بناء "الدوائر" على هذه البتات لحساب العمليات مثل الجمع والضرب. تم تحسين أجهزة الكمبيوتر خصيصًا للأعداد الصحيحة 16 بت و32 بت و64 بت. على سبيل المثال، تم اختيار 2 أس 64 - 2 أس 32 + 1 و2 أس 31 - 1 ليس فقط لأنها تتناسب مع هذه الحدود ولكن أيضًا لأنها تتناسب جيدًا مع هذه الحدود: يمكنك القيام بذلك عن طريق تنفيذ الضرب العادي 32 بت لتنفيذ معامل الضرب 2 64 - 2 32 + 1، ونقل الناتج ونسخه في عدة أماكن؛ تشرح هذه المقالة بعض التقنيات جيدًا.
ومع ذلك، فإن الطريقة الأفضل هي إجراء العمليات الحسابية مباشرةً بالنظام الثنائي. ماذا لو كانت الإضافة "مجرد" XOR دون الحاجة إلى القلق بشأن "حمل" الفائض من إضافة 1 + 1 من بتة إلى أخرى؟ ماذا لو كان من الممكن إجراء الضرب بشكل أكثر توازيًا بنفس الطريقة؟ تعتمد هذه المزايا على القدرة على استخدام بت واحد لتمثيل قيمة صحيحة/خطأ.
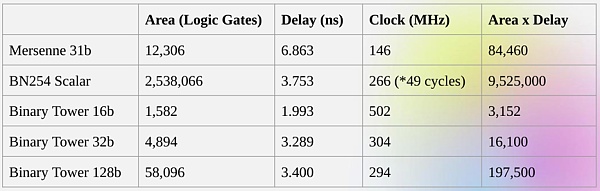
الحصول على هذه المزايا من إجراء الحسابات الثنائية مباشرة هو بالضبط ما يحاول Binius القيام به. أظهر فريق Binius تحسينات في الكفاءة في خطابهم في zkSummit:
 p>
p>
على الرغم من أن "الحجم" هو نفسه تقريبًا، إلا أن العمليات الميدانية الثنائية 32 بت تتطلب موارد حوسبة أقل بخمس مرات من العمليات الميدانية ميرسين 31 بت.
من كثيرات الحدود إلى المكعبات الفائقة
لنفترض أننا نؤمن بهذا المنطق والرغبة في فعل كل شيء باستخدام البتات (0 و1). كيف نعبر عن مليار بت باستخدام كثير الحدود؟
هنا نواجه مشكلتين عمليتين:
لكي تمثل كثيرة الحدود عددًا كبيرًا من القيم، يجب أن تكون هذه القيم قابلة للوصول أثناء تقييم كثيرة الحدود: في مثال فيبوناتشي أعلاه، F(0)، F(1) … F (100)، وفي عملية حسابية أكبر يصل الأس إلى الملايين. يجب أن تحتوي الحقول التي نستخدمها على أرقام تصل إلى هذا الحجم.
إثبات أن أي قيمة نرسلها في شجرة Merkle (مثل جميع STARKs) مطلوبة Reed- يقوم سليمان بتشفيرها: على سبيل المثال، توسيع القيمة من n إلى 8n، وذلك باستخدام التكرار لمنع المُثبِّت الخبيث من الغش عن طريق تزوير قيمة أثناء الحساب. يتطلب هذا أيضًا حقلاً كبيرًا بدرجة كافية: للقياس من مليون قيمة إلى 8 ملايين، تحتاج إلى 8 ملايين نقطة مختلفة لتقييم كثير الحدود.
الفكرة الأساسية لـ Binius هي حل هاتين المشكلتين بشكل منفصل وتمثيل نفس البيانات بطريقتين مختلفتين للوفاء بها . أولا، كثير الحدود نفسه.
أنظمة مثل SNARK القائم على المنحنى الإهليلجي، وSTARK، وPlonky2، وما إلى ذلك، تتعامل عادةً مع كثيرات الحدود في متغير واحد: F(x). من ناحية أخرى، يأخذ Binius الإلهام من بروتوكول Spartan ويستخدم متعددات الحدود متعددة المتغيرات: F(x1,x2,...xk). في الواقع، نحن نمثل المسار الحسابي بأكمله على "المكعب الزائد" الحسابي حيث يكون كل xi إما 0 أو 1. على سبيل المثال، إذا أردنا تمثيل تسلسل فيبوناتشي، وما زلنا نستخدم حقلًا كبيرًا بما يكفي لتمثيلها، فيمكننا التفكير في أول 16 تسلسلًا لها على النحو التالي:

وبعبارة أخرى، F(0 ,0,0, 0) يجب أن تكون 1، F(1,0,0,0) هي أيضًا 1، F(0,1,0,0) هي 2، وهكذا حتى F(1,1,1,1)=987 . بالنظر إلى المكعب الزائد لمثل هذه الحسابات، هناك متعدد الحدود الخطي متعدد المتغيرات (الدرجة 1 لكل متغير) الذي ينتج هذه الحسابات. لذلك يمكننا أن نفكر في هذه المجموعة من القيم باعتبارها تمثيلا لكثيرة الحدود؛ ولسنا بحاجة لحساب المعاملات.
هذا المثال بالطبع للتوضيح فقط: من الناحية العملية، الهدف الأساسي من الدخول في المكعب الفائق هو السماح لنا بالتعامل مع البتات الفردية. تتمثل طريقة "Binius الأصلية" لحساب أرقام فيبوناتشي في استخدام مكعب ذي أبعاد أعلى، باستخدام كل مجموعة مكونة من 16 بت على سبيل المثال لتخزين رقم. يتطلب الأمر بعض البراعة لتنفيذ عملية جمع الأعداد الصحيحة على أساس البت، لكن الأمر ليس صعبًا بالنسبة لـ Binius.
الآن، دعونا نلقي نظرة على رموز المحو. طريقة عمل STARK هي: تأخذ قيم n، ويقوم Reed-Solomon بتوسيعها إلى قيم أكثر (عادةً 8n، عادةً بين 2n و32n)، ثم تختار بشكل عشوائي بعض فروع Merkle من التوسيع وتقوم بشيء ما من نوع التفتيش عليها. طول المكعب الزائد هو 2 في كل بعد. لذلك، فإن توسيعه مباشرة ليس أمرًا عمليًا: لا توجد "مساحة" كافية لأخذ عينة من فرع Merkle من 16 قيمة. إذن ماذا نفعل؟ لنفترض أن المكعب الزائد هو مربع!
Simple Binius - مثال
حول البروتوكول لـ تنفيذ python، يرجى نسخ الرابط أدناه إلى متصفحك لعرضه: https://github.com/ethereum/research/blob/master/binius/simple_binius.py
دعونا نلقي نظرة على مثال، باستخدام الأعداد الصحيحة العادية كحقول لدينا للراحة (في التنفيذ الحقيقي، سيتم استخدام عناصر الحقل الثنائي). أولاً، نقوم بتشفير المكعب الفائق الذي نريد إرساله كمربع:
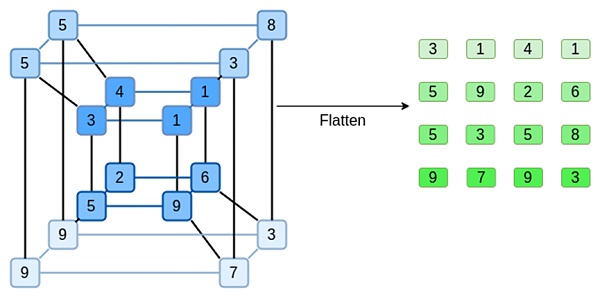
الآن، نقوم بتمديد المربع باستخدام Reed-Solomon. أي أننا نتعامل مع كل صف على أنه كثيرة حدود من الدرجة الثالثة يتم تقييمها عند x = {0,1,2,3}، ونقيم نفس كثيرة الحدود عند x = {4,5,6,7}:

كن حذرًا، الأرقام يمكن أن تتضخم بسرعة! لهذا السبب نستخدم دائمًا في التطبيقات الحقيقية الحقول المحدودة، وليس الأعداد الصحيحة العادية: إذا استخدمنا الأعداد الصحيحة modulo 11، على سبيل المثال، فإن امتداد السطر الأول سيكون فقط [3,10,0,6].
إذا كنت تريد تجربة الامتداد والتحقق من الأرقام هنا بنفسك، فيمكنك استخدام كود الامتداد البسيط الخاص بي Reed-Solomon هنا.
بعد ذلك، نتعامل مع هذا الامتداد كعمود وننشئ شجرة Merkle للعمود. جذور شجرة ميركل هي التزاماتنا.
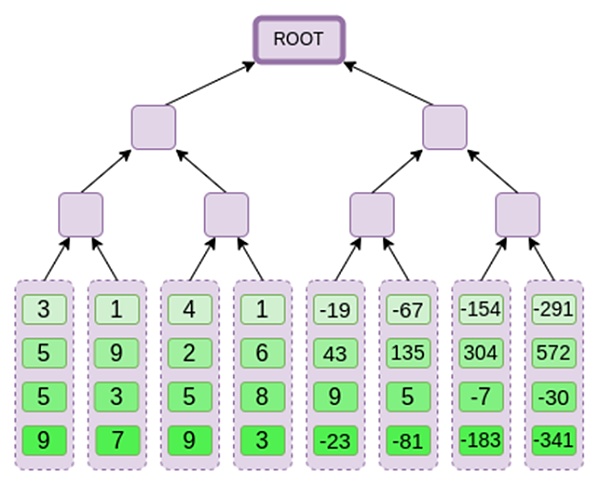
الآن، لنفترض أن المثل يريد أن يثبت في مرحلة ما حساب كثير الحدود هذا r={r0,r1,r2,r3}. هناك اختلاف دقيق في Binius يجعله أضعف من مخططات الالتزام متعددة الحدود الأخرى: لا ينبغي للممثل أن يعرف أو يكون قادرًا على تخمين s قبل الالتزام بجذور Merkle (وبعبارة أخرى، يجب أن تكون r قيمة عشوائية زائفة). وهذا يجعل المخطط عديم الفائدة في "عمليات البحث في قاعدة البيانات" (على سبيل المثال، "حسنًا، لقد أعطيتني جذر Merkle، والآن أثبت لي P(0,0,1,0)!").
لكن بروتوكولات إثبات المعرفة الصفرية التي نستخدمها فعليًا لا تتطلب عادةً "عمليات بحث في قاعدة البيانات"؛ بل تحتاج فقط إلى التحقق من كثير الحدود عند نقطة تقييم عشوائية. ولذلك، فإن هذا التقييد يخدم أغراضنا.
لنفترض أننا اخترنا r={1,2,3,4} (نتيجة حساب متعدد الحدود هي -137 في الوقت الحالي؛ يمكنك استخدام هذا الرمز للتأكيد ) . والآن ندخل في عملية الإثبات. نقسم r إلى جزأين: الجزء الأول {1,2} يمثل المجموعة الخطية للأعمدة داخل الصف، والجزء الثاني {3,4} يمثل المجموعة الخطية للصفوف. نحسب "منتج الموتر" لجزء العمود:
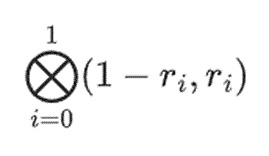 < /p>
< /p>
بالنسبة لجزء الخط:

وهذا يعني: قائمة بجميع المنتجات المحتملة ذات القيمة في كل مجموعة. في حالة الصف نحصل على:
[(1-r2)*(1-r3), (1-r3), (1-r2)* r3 , r2*r3]
استخدم r={1,2,3,4} (لذلك r2=3 و r3=4):
< نمط p = "محاذاة النص: يسار؛">[(1-3)*(1-4)، 3*(1-4)،(1-3)*4,3*4] = [6، - 9 -8 -12]الآن، نقوم بحساب "صف" جديد عن طريق أخذ مجموعة خطية من الصفوف الموجودة. بمعنى آخر نأخذ:
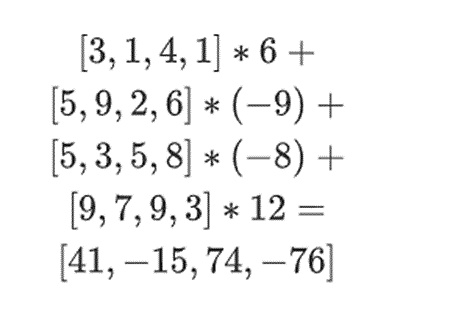
يمكنك اعتبار ما يحدث هنا بمثابة تقييم جزئي. إذا قمنا بضرب منتج الموتر الكامل في المتجه الكامل لجميع القيم، فستحصل على الحساب P(1,2,3,4) = -137. نحن هنا نضرب منتجات الموتر الجزئي باستخدام نصف الإحداثيات التي تم تقييمها فقط ونقوم بتقليل شبكة القيمة N إلى صف من قيم الجذر N. إذا أعطيت هذا الخط لشخص آخر، فيمكنه إجراء بقية الحساب باستخدام حاصل ضرب الموتر للنصف الآخر من الإحداثيات التي تم تقييمها.
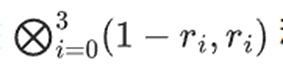
يزود المثبت المدقق بإثبات Merkle للصف الجديد التالي: t وبعض الأعمدة التي تم أخذ عينات منها بشكل عشوائي. في مثالنا التوضيحي، سنطلب من المُثبِّت توفير العمود الأخير فقط؛ وفي الحياة الواقعية، سيحتاج المُثبِّت إلى توفير عشرات الأعمدة لتحقيق الأمان الكافي.
الآن، نستفيد من خطية كود Reed-Solomon. الخاصية الرئيسية التي نستخدمها هي: أخذ تركيبة خطية من تمديد ريد-سولومون يعطي نفس النتيجة مثل تمديد ريد-سولومون من التركيبة الخطية. يحدث "استقلال النظام" هذا عادةً عندما تكون كلتا العمليتين خطيتين.
يقوم المدققون بهذا بالضبط. لقد قاموا بحساب مجموعات t والمجموعات الخطية من نفس الأعمدة التي حسبها المُبرِح من قبل (ولكن فقط الأعمدة التي قدمها المُثبِّت)، وتحققوا من أن كلا الإجراءين أعطى نفس الإجابة.
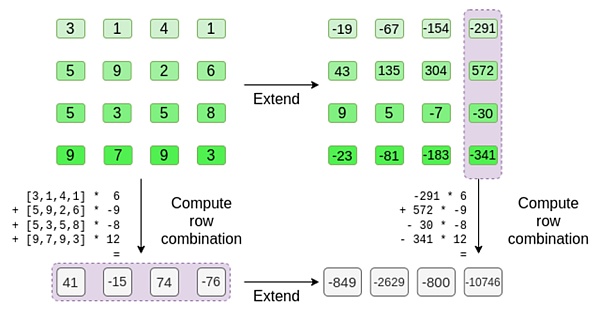
في هذه الحالة، تمديد t، وحساب نفس التركيبة الخطية ([6,-9,-8,12]، كلاهما يعطي نفس الإجابة: -10746. وهذا يثبت أن جذور ميركل مبنية على "النوايا الطيبة" ( أو على الأقل "قريب بدرجة كافية")، وهو يطابق t: على الأقل الغالبية العظمى من الأعمدة متوافقة مع بعضها البعض
ولكن هناك التحقق من الصحة الشيء الذي يحتاج المدقق إلى التحقق منه: التحقق من تقييم متعدد الحدود {r0…r3}. جزء" من نقطة الحساب:
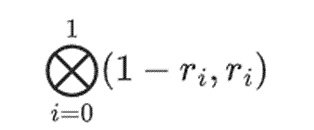
في مثالنا، حيث r={1,2,3,4} لذا فإن نصف العمود المحدد هو {1,2})، وهذا يساوي:
< p style="text-align:center">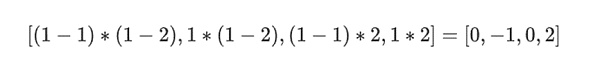
الآن نحن خذ هذه المجموعة الخطية t:
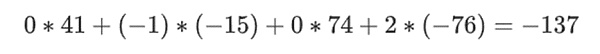 < /p>
< /p>
هذه هي نفس نتيجة الحل المباشر لكثيرة الحدود.
ما ورد أعلاه قريب جدًا من الوصف الكامل لبروتوكول Binius "البسيط". يتمتع هذا بالفعل ببعض المزايا المثيرة للاهتمام: على سبيل المثال، بما أن البيانات مقسمة إلى صفوف وأعمدة، فأنت تحتاج فقط إلى حقل واحد بنصف الحجم. ومع ذلك، فإن هذا لا يدرك الفوائد الكاملة للحوسبة الثنائية. لهذا نحن بحاجة إلى بروتوكول Binius الكامل. لكن أولاً، دعونا نلقي نظرة أعمق على الحقول الثنائية.
حقل ثنائي
أصغر مجال ممكن هو المجال الحسابي الوحدة 2. إنها صغيرة جدًا، يمكننا كتابة جداول الجمع والضرب الخاصة بها:
يمكننا الحصول على حقول ثنائية أكبر بالامتداد: إذا بدأنا من F2 (عدد صحيح modulo 2) فحدد x حيث x تربيع = x +1، نحصل على جدولي الجمع والضرب التاليين:
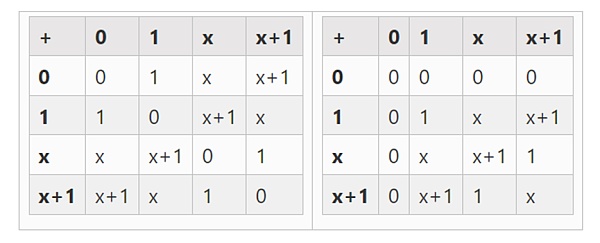
اتضح أنه يمكننا توسيع نطاق الحقل الثنائي إلى حجم كبير بشكل تعسفي من خلال تكرار هذا البناء. على عكس الأعداد المركبة على الأعداد الحقيقية، حيث يمكنك إضافة عنصر جديد، ولكن ليس المزيد من العناصر I (الكواتيرونات موجودة، لكنها غريبة رياضيًا، على سبيل المثال ab لا يساوي ba)، استخدم الحقول المحدودة، يمكنك دائمًا إضافة جديد ملحقات. على وجه التحديد، تعريفنا للعناصر هو كما يلي:
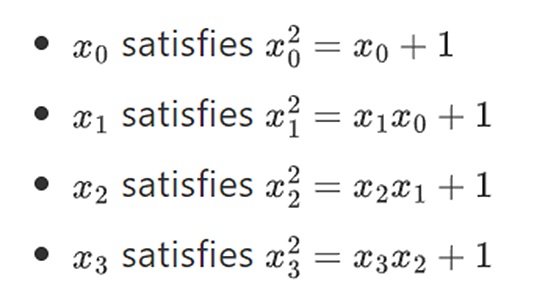
انتظر... يُشار إلى هذا غالبًا باسم هيكل البرج لأنه يمكن اعتبار كل امتداد متتالي بمثابة إضافة طبقة جديدة إلى البرج. هذه ليست الطريقة الوحيدة لإنشاء حقول ثنائية ذات حجم عشوائي، ولكنها تتمتع ببعض المزايا الفريدة التي يستفيد منها Binius.
يمكننا تمثيل هذه الأرقام كقائمة من البتات. على سبيل المثال، 1100101010001111. يمثل البت الأول مضاعفًا للرقم 1، ويمثل البت الثاني مضاعفًا لـ x0، ثم تمثل البتات اللاحقة مضاعفات أرقام x1 التالية: x1، x1*x0، x2، x2*x0، وهكذا. يعد هذا التشفير رائعًا لأنه يمكنك تقسيمه:
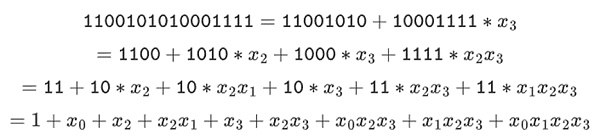
هذا تدوين غير شائع نسبيًا، لكني أحب تمثيل عناصر الحقل الثنائي كأعداد صحيحة، باستخدام تمثيل البت الأكثر كفاءة مع البتات الموجودة على اليمين. أي 1=1، x0=01=2، 1+x0=11=3، 1+x0+x2=11001000 =19، وهكذا. وفي هذا التعبير هو 61779.
عملية الجمع في الحقل الثنائي هي XOR فقط (بالمناسبة، كما هو الحال مع الطرح)؛ لضرب عنصرين x*y، هناك خوارزمية عودية بسيطة جدًا: قم بتقسيم كل رقم إلى نصفين:

ثم قم بتقسيم الضرب:
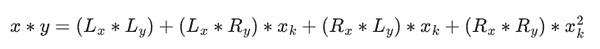
الجزء الأخير هو الجزء الوحيد الصعب بعض الشيء لأنه يتعين عليك التقديم قواعد التبسيط. هناك طرق أكثر فعالية للقيام بالضرب، على غرار خوارزمية كاراتسوبا وتحويل فورييه السريع، لكنني سأترك ذلك كتمرين للقارئ المهتم ليكتشفه.
يتم القسمة في الحقول الثنائية من خلال الجمع بين الضرب والعكس. طريقة الانعكاس "البسيطة ولكن البطيئة" هي تطبيق لنظرية فيرما الصغيرة المعممة. هناك أيضًا خوارزمية انعكاس أكثر تعقيدًا ولكنها أكثر كفاءة والتي يمكنك العثور عليها هنا. يمكنك استخدام الكود هنا للعب مع الجمع والضرب والقسمة للحقول الثنائية.
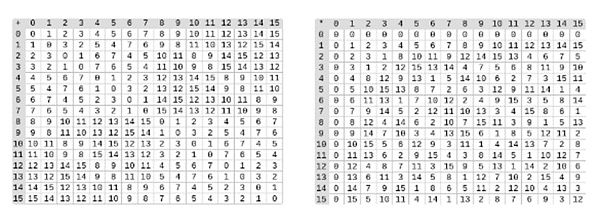
△ على اليسار: جدول إضافة لعناصر الحقل الثنائي المكونة من أربعة أرقام (أي 1 فقط، x0، x1، x0x1). على اليمين: جدول الضرب لعناصر الحقل الثنائي المكونة من أربعة أرقام.
إن جمال هذا النوع من الحقول الثنائية هو أنه يجمع بعضًا من أفضل أجزاء الأعداد الصحيحة "العادية" والحساب المعياري. مثل الأعداد الصحيحة العادية، عناصر الحقل الثنائي غير محدودة: يمكنك توسيعها حسب الرغبة. ولكن تمامًا مثل حساب modulo، إذا كنت تعمل على قيم ضمن حد حجم معين، فستبقى جميع نتائجك أيضًا ضمن نفس النطاق. على سبيل المثال، إذا أخذت 42 قوة متتالية، تحصل على:
 < /p >
< /p >
بعد 255 خطوة، تعود إلى 42 مرفوعًا للأس 255 = 1. تمامًا مثل الأعداد الصحيحة الموجبة والحساب المعياري، فإنها تتبع القوانين الرياضية المعتادة: *b= b*a، a*(b+c)=a*b+a*c، وحتى بعض القوانين الجديدة الغريبة.
أخيرًا، تسهل الحقول الثنائية التعامل مع البتات: إذا كنت تقوم بعمليات حسابية باستخدام أرقام تناسب 2 مرفوعًا للأس k، فإن كل مخرجاتك ستكون مناسبة أيضًا 2 إلى بت الطاقة k. وهذا يتجنب الإحراج. في EIP-4844 الخاص بـ Ethereum، يجب أن تكون كل "كتلة" من النقطة عبارة عن وحدة رقمية، لذا يتطلب تشفير البيانات الثنائية التخلص من بعض المساحة وإجراء فحص A إضافي للتأكد من أن كل عنصر يخزن قيمة أقل من 2 أس 248.
وهذا يعني أيضًا أن العمليات الميدانية الثنائية تتم بسرعة فائقة على أجهزة الكمبيوتر - سواءً وحدات المعالجة المركزية أو تصميمات FPGA وASIC المثالية نظريًا.
ما يعنيه كل هذا هو أنه يمكننا فعل ما فعلناه بترميز Reed-Solomon أعلاه، بطريقة تتجنب تمامًا "انفجار" الأعداد الصحيحة، مثل ما رأيناه في مثالنا، وبطريقة "أصلية" للغاية، هو نوع الحساب الذي تجيده أجهزة الكمبيوتر. تعد خاصية "التقسيم" للحقول الثنائية - كيف نفعل ذلك 1100101010001111=11001010+10001111*x3 ثم تقسيمها وفقًا لاحتياجاتنا أمرًا بالغ الأهمية أيضًا لتحقيق قدر كبير من المرونة.
إكمال Binius
تنفيذ بروتوكول بايثون، من فضلك انسخ الرابط أدناه إلى متصفحك لعرضه: https://github.com/ethereum/research/blob/master/binius/packed_binius.py
الآن، يمكننا الانتقال إلى "Full Binius"، الذي يكيف "Simple Binius" من أجل (i) العمل على الحقول الثنائية و (ii) دعونا نلتزم بت واحد. من الصعب فهم هذا البروتوكول لأنه ينتقل ذهابًا وإيابًا بين الطرق المختلفة للنظر إلى مصفوفة البتات؛ وبالطبع استغرق فهمه وقتًا أطول مما يستغرقه عادةً فهم بروتوكولات التشفير. ولكن بمجرد فهم الحقول الثنائية، فإن الخبر السار هو أن "الرياضيات الأصعب" التي يعتمد عليها Binius غير موجودة.
هذا ليس اقتران منحنى إهليلجي، حيث توجد ثقوب أرنب في الهندسة الجبرية للحفر هنا، تحتاج فقط إلى حقول ثنائية.
دعونا نلقي نظرة أخرى على المخطط الكامل:

الآن، يجب أن تكون على دراية بمعظم المكونات. فكرة "تسوية" المكعب الفائق إلى شبكة، وفكرة حساب مجموعات الصفوف ومجموعات الأعمدة كمنتجات موتر لنقاط التقييم، واختبار "توسيع ريد-سولومون ثم حساب مجموعات الصفوف" و"حساب مجموعات الصفوف" ومن ثم ريد- يتم تنفيذ فكرة التكافؤ بين امتدادات سليمان في Binius البسيط.
ما الجديد في "Complete Binius"؟ في الأساس ثلاثة أشياء:
يجب أن تكون القيم الفردية في المكعب الفائق والمربع بت( 0 أو 1).
تقوم عملية التوسيع بتوسيع البتات إلى المزيد عن طريق تجميعها في أعمدة وافتراض أنها عناصر حقل أكبر بشكل مؤقت.
بعد خطوة تجميع الصف، هناك خطوة "تحلل إلى بتات" خاصة بالعنصر والتي تحول التوسع مرة أخرى إلى بتات.
سنناقش هذين الموقفين تباعًا. أولاً، عملية التمديد الجديدة. يحتوي كود Reed-Solomon على قيود أساسية، إذا كنت تريد تمديد n إلى k*n، فأنت بحاجة إلى العمل في الحقول ذات قيم k*n المختلفة التي يمكن استخدامها كإحداثيات. لا يمكنك فعل ذلك باستخدام F2 (المعروف أيضًا باسم bit). إذن ما نقوم به هو "تجميع" عناصر F2 المجاورة معًا لتكوين قيمة أكبر. في المثال هنا، قمنا بتجميع قطعتين في المرة الواحدة في عناصر {0، 1، 2، 3}، وهو ما يكفي بالنسبة لنا نظرًا لأن الامتداد الخاص بنا يحتوي على أربع نقاط حسابية فقط. في الدليل "الحقيقي"، قد نعيد 16 بت في المرة الواحدة. نقوم بعد ذلك بتنفيذ كود Reed-Solomon على هذه القيم المجمعة وتفكيكها إلى أجزاء مرة أخرى.

الآن، مجموعات الصفوف. من أجل جعل فحص "التقييم عند نقطة عشوائية" آمنًا من الناحية التشفيرية، نحتاج إلى أخذ عينة من النقطة من مساحة كبيرة إلى حد ما (أكبر بكثير من المكعب الفائق نفسه). لذلك، في حين أن النقاط الموجودة داخل المكعب الفائق هي بتات، فإن القيم المحسوبة خارج المكعب الفائق ستكون أكبر بكثير. في المثال أعلاه، تصبح "مجموعة الصفوف" [11,4,6,1].
هذا يثير مشكلة: نحن نعرف كيفية دمج البتات في قيمة أكبر، ثم إجراء توسيع Reed-Solomon على هذا الأساس، ولكن ماذا عن القيام بذلك؟ نفس الشيء بالنسبة لأزواج القيمة الأكبر؟
خدعة Binius هي العمل على أساس البت: فنحن ننظر إلى بت واحد من كل قيمة (على سبيل المثال: بالنسبة لشيء نسميه "11"، أي [1, 1,0,1] ) ثم قم بالتوسيع حسب الصف. تنفيذ عملية التوسيع على الكائن. أي أننا نقوم بعملية التوسيع على صف واحد من كل عنصر، ثم على الصف x0، ثم على الصف "x1"، ثم على الصف x0x1، وهكذا (حسنًا، في مثال لعبتنا، توقفنا عند هذا الحد، ولكن في التنفيذ الحقيقي سنصل إلى 128 سطرًا (آخر سطر هو x6*…*x0 ))
المراجعة
مراجعة
strong>نقوم بتحويل البتات الموجودة في المكعب الفائق إلى شبكة، ثم نتعامل مع مجموعات البت المتجاورة في كل صف كعناصر حقل أكبر ونجري عمليات حسابية عليها حتى يقوم Reed-Solomon بتوسيع الصفوف.
بعد ذلك، نأخذ مجموعة الصفوف من البتات لكل عمود ونحصل على عمود البت لكل صف كمخرجات (أصغر بكثير للمربعات الأكبر من 4x4).
أخيرًا، نتعامل مع المخرجات كمصفوفة وبتاتها كصفوف.
لماذا هذا؟ في الرياضيات "العادية"، إذا بدأت في تقطيع رقم إلى بتات، فإن القدرة (عادة) على إجراء عمليات خطية بأي ترتيب والحصول على نفس النتيجة تنهار.
على سبيل المثال، إذا بدأت بالرقم 345 وضربته في 8 ثم في 3، أحصل على 8280. وإذا عكست هاتين العمليتين، فإنني احصل أيضًا على 8280. لكن إذا قمت بإدراج عملية "تقسيم على بت" بين الخطوتين، فسوف تتعطل: إذا قمت بإجراء 8x، ثم 3x، فستحصل على:
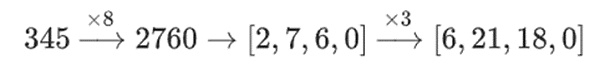
ولكن إذا قمت بذلك 3 مرات، فافعل ذلك 8 مرات وستحصل على :
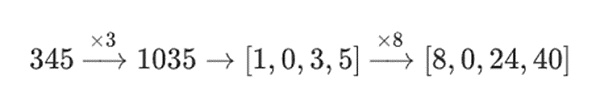
ولكن في الحقل الثنائي المبني ببنية برجية، ينجح هذا الأسلوب. السبب يكمن في قابلية الفصل بينهما: إذا قمت بضرب قيمة كبيرة بقيمة صغيرة، فإن ما يحدث في كل مقطع يبقى على كل مقطع. إذا ضربنا 1100101010001111 في 11، فهذا هو نفس التحلل الأول لـ 1100101010001111، وهو

ثم اضرب كل مكون في 11 على التوالي.
ضعها معًا
بشكل عام، المعرفة صفر تعمل أنظمة الإثبات عن طريق تقديم عبارات حول كثيرات الحدود التي تمثل في الوقت نفسه عبارات حول التقييم الأساسي: كما رأينا في مثال فيبوناتشي، F(X+2)-F(X+1) -F(X) = Z(X)*H (X) يتحقق من جميع خطوات حساب فيبوناتشي في وقت واحد. نحن نتحقق من البيانات حول كثيرات الحدود من خلال إثبات التقييم في نقاط عشوائية. يمثل هذا التحقق من النقاط العشوائية فحصًا لمتعددة الحدود بأكملها: إذا كانت معادلة متعددة الحدود غير متطابقة، فهناك احتمال ضئيل أن تتطابق عند إحداثيات عشوائية محددة.
في الممارسة العملية، أحد الأسباب الرئيسية لعدم الكفاءة هو أنه في البرامج الحقيقية، تكون معظم الأرقام التي نتعامل معها صغيرة: فهارس في الحلقات، صحيح / القيم الكاذبة والعدادات وأشياء مماثلة. ومع ذلك، عندما نستخدم ترميز Reed-Solomon "لتوسيع" البيانات لتوفير التكرار اللازم لجعل عمليات التحقق المستندة إلى إثبات Merkle آمنة، فإن معظم القيم "الإضافية" تنتهي في النهاية بشغل حجم الحقل بالكامل، حتى إذا كانت القيمة الأصلية صغيرة.
لحل هذه المشكلة، نريد أن نجعل هذا الحقل صغيرًا قدر الإمكان. يأخذنا Plonky2 من أرقام 256 بت إلى أرقام 64 بت، ثم يسقطها Plonky3 إلى أرقام 31 بت. ولكن حتى هذا ليس الأمثل. باستخدام الحقول الثنائية، يمكننا التعامل مع بت واحد. وهذا يجعل التشفير "كثيفًا": إذا كانت بياناتك الأساسية الفعلية تحتوي على n بت، فسيكون التشفير الخاص بك n بت وسيكون الامتداد 8 * n بت، دون أي حمل إضافي.
الآن، دعونا نلقي نظرة على المخطط مرة ثالثة:

في Binius، نعمل على متعدد الحدود متعدد الخطوط: مكعب مفرط P(x0, x1,... xk)، حيث يقوم تقييم واحد P(0,0,0,0), P(0,0,0,1) حتى P(1,1,1,1) بحفظ البيانات التي نهتم بها. لتوضيح العملية الحسابية عند نقطة معينة، نقوم "بإعادة تفسير" نفس البيانات على أنها مربع. نقوم بعد ذلك بتوسيع كل صف باستخدام تشفير Reed-Solomon لتوفير تكرار البيانات المطلوبة لأمان استعلامات فرع Merkle العشوائية. نقوم بعد ذلك بحساب مجموعات خطية عشوائية من الصفوف، وتصميم المعاملات بحيث تحتوي الصفوف المدمجة الجديدة بالفعل على القيم المحسوبة التي نهتم بها. يتم تمرير هذا الصف الذي تم إنشاؤه حديثًا (أعيد تفسيره إلى 128 بت صفًا) وبعض الأعمدة المحددة عشوائيًا مع فرع Merkle إلى أداة التحقق.
بعد ذلك، يقوم المدقق بإجراء "مجموعة الصفوف الموسعة" (أو بشكل أكثر دقة، مجموعة الصفوف الموسعة) و"توسيع مجموعة الصفوف"، و التحقق من تطابق الاثنين. ثم قم بحساب مجموعة الأعمدة وتحقق مما إذا كانت تُرجع القيمة التي يطالب بها المُثبت. هذا هو نظام الإثبات الخاص بنا (أو بالأحرى، نظام الالتزام متعدد الحدود، وهو المكون الرئيسي لنظام الإثبات).
ما الذي لم نغطيه بعد؟
خوارزمية فعالة لتوسيع الصفوف، والتي تم تحسينها بالفعل في حسابات أداة التحقق من الصحة ضرورية من أجل الكفاءة. نحن نستخدم تحويل فورييه السريع في الحقول الثنائية، الموصوفة هنا (على الرغم من أن التنفيذ الدقيق سيختلف، حيث تستخدم هذه المقالة بنية أقل كفاءة لا تعتمد على التوسع العودي).
الحساب. تعد كثيرات الحدود أحادية المتغير ملائمة لأنه يمكنك القيام بأشياء مثل F(X+2)-F(X+1)-F(X) = Z(X)*H(X) لربط الخطوات المتجاورة في الحساب. في المكعب الفائق، تكون "الخطوة التالية" أقل قابلية للتفسير بكثير من "X+1". يمكنك القيام بـ X+k، أي قوى k، لكن سلوك القفز هذا سيضحي بالعديد من المزايا الرئيسية لـ Binius. الحل معروض في ورقة Binius. (انظر القسم 4.3)، ولكن هذه حفرة عميقة في حد ذاتها.
كيفية إجراء عمليات فحص قيمة محددة بأمان. يتطلب مثال فيبوناتشي التحقق من شروط الحدود الرئيسية: F(0)=F(1)=1 وقيمة F(100). ولكن مع Binius "الخام"، ليس من الآمن التحقق من نقاط الحساب المعروفة. هناك بعض الطرق البسيطة إلى حد ما لتحويل فحص حسابي معروف إلى فحص حسابي غير معروف، باستخدام ما يسمى ببروتوكول التحقق من المبلغ، لكننا لن نغطي تلك الطرق هنا.
يستخدم بروتوكول البحث، وهو أسلوب آخر أصبح مستخدمًا على نطاق واسع مؤخرًا، لإنشاء بحث فائق الكفاءة نظام إثبات. يمكن استخدام Binius مع العديد من بروتوكولات البحث عن التطبيقات.
ما بعد وقت التحقق من الجذر التربيعي. الجذور التربيعية غالية الثمن: يبلغ طول إثبات Bit’s Binius للقوة 2 أس 32 حوالي 11 ميغابايت. يمكنك التعويض عن هذه المشكلة عن طريق استخدام أنظمة إثبات أخرى لعمل "براهين لبراهين Binius"، وبالتالي الحصول على كفاءة براهين Binius وحجم إثبات أصغر. هناك خيار آخر وهو بروتوكول FRI-binius الأكثر تعقيدًا، والذي ينشئ برهانًا متعدد اللوغاريتمات (تمامًا مثل FRI العادي).
كيف يؤثر Binius على "ملاءمة SNARK". الملخص الأساسي هو أنه إذا كنت تستخدم Binius، فلن تحتاج بعد الآن إلى القلق بشأن إجراء عملية حسابية "صديقة للحساب": التجزئة "العادية" لم تعد أكثر كفاءة من التجزئة الحسابية التقليدية، أو معامل الضرب 2 أس 32 أو مودولو 2 256 لم يعد يمثل صداعًا مقارنة بمعامل الضرب، وما إلى ذلك. لكن هذا موضوع معقد. تتغير الكثير من الأشياء عندما يتم كل شيء بطريقة ثنائية.
آمل أن يكون هناك المزيد من التحسينات على تقنيات الإثبات الثنائية المستندة إلى الحقل في الأشهر المقبلة.
تتضمن "محاذاة الإيثيريوم" توافق القيمة، ومواءمة التكنولوجيا، والمواءمة الاقتصادية، وما إلى ذلك.
 JinseFinance
JinseFinanceالشرط الأساسي لفهم هذه المقالة هو أنك تفهم بالفعل المبادئ الأساسية لـ SNARKs وSTARKs. إذا لم تكن على دراية بهذا، أقترح عليك قراءة الأجزاء القليلة الأولى من هذه المقالة لفهم الأساسيات.
 JinseFinance
JinseFinanceETH، تفسير أحدث مقال لـ Vitalik Golden Finance، يكمن هنا روح Ethereum وجوهر عالم العملات المشفرة.
 JinseFinance
JinseFinanceتعاون Vitalik مع أربعة مؤلفين مشاركين لكشف النقاب عن ورقة بحثية تقدم أعجوبة تكنولوجية تُعرف باسم "مجمعات الخصوصية"، المصممة لمعالجة واحدة من أكثر القضايا إلحاحًا في مجال blockchain.
 Catherine
Catherineيتضمن التحديث الجديد "البلاء" الذي سيساعد في حل مشكلات MEV.
 Beincrypto
Beincryptoيا له من عقد من المقالات - تغطي كل شيء من الرموز المميزة لـ Soulbound إلى DAOs الفائقة - يقول عن Ethereum والتشفير.
 Coindesk
Coindeskتحدث مخترع Ethereum Vitalik Buterin ووالده Dmitry “Dima” Buterin عن سوق العملات المشفرة وتقلبها والمضاربين. ...
 Bitcoinist
Bitcoinist与PoW相比,PoS是一个更好的区块链安全机制。
 链向资讯
链向资讯与PoW相比,PoS是一个更好的区块链安全机制。
 Ftftx
Ftftxبدأت الدولة الصغيرة الواقعة في جنوب شرق أوروبا في غربلة المياه العكرة لتنظيم blockchain من خلال منح الجنسية المؤسس المشارك لشركة Ethereum.
 Cointelegraph
Cointelegraph