العنوان الأصلي: "استكشاف دائرة STARKs" بقلم: فيتاليك بوتيرين، المؤسس المشارك لـ Ethereum جمعه: كريس، Techub News
الشرط الأساسي لفهم هذه المقالة هو أنك تفهم بالفعل المبادئ الأساسية لـ SNARKs وSTARKs. إذا لم تكن على دراية بهذا، أقترح عليك قراءة الأجزاء القليلة الأولى من هذه المقالة لفهم الأساسيات.
في السنوات الأخيرة، كان الاتجاه في تصميم بروتوكول STARKs نحو استخدام حقول أصغر. استخدمت تطبيقات الإنتاج الأقدم لـ STARKs حقول 256 بت، أي الحساب المعياري على الأعداد الكبيرة (على سبيل المثال 21888...95617)، مما جعل هذه البروتوكولات متوافقة مع التوقيعات القائمة على المنحنى الإهليلجي. ومع ذلك، فإن كفاءة هذا التصميم منخفضة نسبيًا في الظروف العادية، فإن معالجة وحساب هذه الأعداد الكبيرة ليس لها أي استخدام عملي، وسوف تهدر الكثير من الطاقة الحاسوبية، مثل معالجة X (التي تمثل رقمًا معينًا) ومعالجة أربع مرات X. ، المعالجة مطلوبة فقط تسع الوقت الحسابي. لحل هذه المشكلة، بدأت STARKs في الانتقال إلى مجالات أصغر: أولاً Goldilocks، ثم Mersenne31 وBabyBear.
لقد أدى هذا التحول إلى تحسين سرعات الإثبات، مثل قدرة Starkware على إثبات 620.000 تجزئة Poseidon2 في الثانية على كمبيوتر محمول M3. وهذا يعني أنه طالما أننا على استعداد للثقة في Poseidon2 كوظيفة تجزئة، فيمكننا حل المشكلة الصعبة المتمثلة في تطوير ZK-EVM الفعال. فكيف تعمل هذه التقنيات؟ كيف يمكن بناء هذه البراهين على حقول أصغر؟ كيف يمكن مقارنة هذه البروتوكولات بحلول مثل Binius؟ ستستكشف هذه المقالة هذه التفاصيل، مع التركيز بشكل خاص على مخطط يسمى Circle STARKs (في برنامج Starkware، وPolygon's Plonky3 والإصدار الخاص بي المطبق في Python)، والذي يحتوي على نفس الخصائص الفريدة المتوافقة مع حقل Mersenne31.
المشكلات الشائعة عند العمل مع حقول رياضية أصغر
عند إنشاء حرف A مستند على التجزئة مهم جدًا الحيلة عند عمل البراهين (أو البراهين من أي نوع) هي أن تكون قادرًا على التحقق بشكل غير مباشر من خصائص كثيرة الحدود من خلال إثبات تقييمها في نقاط عشوائية. هذا الأسلوب يمكن أن يبسط عملية الإثبات إلى حد كبير، حيث أن التقييم في نقاط عشوائية عادة ما يكون أسهل بكثير من التعامل مع كثيرة الحدود بأكملها.
على سبيل المثال، لنفترض أن نظام الإثبات يتطلب منك إنشاء التزام بكثيرة الحدود، A، التي يجب أن تلبي A^3 (x) + x - A ( \omega* x) = x^N (نوع إثبات شائع جدًا في بروتوكول ZK-SNARK). يمكن أن يطلب منك البروتوكول اختيار إحداثيات عشوائية وإثبات أن A (r) + r - A (\omega*r) = r^N. ثم ارجع إلى A (r) = c، وأثبت أن Q = \frac {A - c}{X - r} كثيرة الحدود.
إذا فهمت التفاصيل أو الآليات الداخلية للبروتوكولات مسبقًا، فقد تتمكن من إيجاد طرق لتجاوزها أو كسرها. يمكن ذكر الإجراءات أو الأساليب المحددة لتحقيق ذلك بعد ذلك. على سبيل المثال، لتحقيق المعادلة A (\omega * r)، يمكنك ضبط A (r) على 0 وجعل A خطًا مستقيمًا عبر هاتين النقطتين.
لمنع هذه الهجمات، نحتاج إلى اختيار r بعد أن يقوم المهاجم بتوفير A (Fiat-Shamir هي تقنية تستخدم لتعزيز أمان البروتوكول، لتجنب الهجمات عن طريق تعيين معلمات معينة على قيم تجزئة معينة. يجب أن تكون المعلمات المحددة من مجموعة كبيرة بما يكفي لضمان عدم قدرة المهاجمين على التنبؤ بهذه المعلمات أو تخمينها، وبالتالي تحسين أمان النظام : left;">في البروتوكولات المستندة إلى منحنى بيضاوي وSTARKs في فترة 2019، تكون المشكلة بسيطة: يتم تنفيذ جميع عملياتنا الحسابية على أرقام 256 بت، لذلك يمكننا اختيار r ليكون رقمًا عشوائيًا 256 بت، وهذا أمر جيد، ومع ذلك، في STARKs في الحقول الأصغر، نواجه مشكلة: لا يوجد سوى حوالي 2 مليار قيمة محتملة لـ r للاختيار من بينها، لذلك يحتاج المهاجم إلى تجربة 2 مليار فقط على الرغم من أن حجم العمل ضخم، إلا أنه لا يزال ممكنًا بالنسبة للمهاجم المصمم.
هناك حلان لهذه المشكلة:
فحوصات عشوائية متعددة
الحقول الموسعة
يتم تنفيذها عدة مرات. طريقة الفحص العشوائي هي الأبسط والأكثر فعالية: بدلاً من التحقق من إحداثي واحد، من الممكن تكرار التحقق على أربعة إحداثيات عشوائية، ولكن هناك مشكلات تتعلق بالكفاءة إذا كنت تتعامل مع درجة أصغر من قيمة معينة لكثيرات الحدود، وتعمل على مجال بحجم معين، فيمكن للمهاجم في الواقع إنشاء كثيرات حدود ضارة يبدو الأمر طبيعيًا في هذه المواقع، لذا فإن ما إذا كان بإمكانهم كسر البروتوكول بنجاح هو سؤال احتمالي، ويجب زيادة عدد جولات الفحص لتعزيز الأمن العام وضمان الدفاع الفعال ضد المهاجمين. text-align: left;">وهذا يؤدي إلى حل آخر: توسيع المجال. الحقل الممتد يشبه الأعداد المركبة، ولكنه يعتمد على الحقل المحدود. نقدم قيمة جديدة، يُشار إليها بـ α\alphaα، و أعلن أنها تلبي علاقة معينة، مثل α2=some value\alpha^2 = \text {some value}α2=some value. وبهذه الطريقة، نقوم بإنشاء بنية رياضية جديدة قادرة على إجراء عمليات أكثر تعقيدًا في الحقول المحدودة. في هذا المجال الممتد، يصبح حساب الضرب ضربًا باستخدام القيمة الجديدة α\alphaα. يمكننا الآن العمل على أزواج من القيم في مجال موسع، وليس مجرد أرقام مفردة. على سبيل المثال، إذا كنا نعمل في مجال مثل Mersenne أو BabyBear، فإن هذا الامتداد يسمح لنا بالحصول على المزيد من خيارات القيمة، وبالتالي تحسين الأمان. لزيادة حجم الحقل بشكل أكبر، يمكننا تطبيق نفس التقنية بشكل متكرر. نظرًا لأننا استخدمنا بالفعل α\alphaα، فنحن بحاجة إلى تحديد قيمة جديدة، والتي يتم تمثيلها في Mersenne31 باختيار α\alphaα بحيث تكون α2=some value\alpha^2 = \text {some value}α2=some value.

الكود (يمكنك تحسينه باستخدام Karatsuba )
من خلال توسيع الحقل، لدينا الآن ما يكفي من القيم للاختيار من بينها والتي تلبي احتياجاتنا الأمنية. إذا كنت تتعامل مع متعددات الحدود بدرجة أقل من ddd، فهذا يوفر 104 بت من الأمان في كل جولة. وهذا يعني أن لدينا الأمن الكافي. إذا كان هناك حاجة إلى مستوى أمان أعلى، مثل 128 بت، فيمكننا إضافة بعض الأعمال الحسابية الإضافية إلى البروتوكول لتعزيز الأمان.
يتم استخدام المجال الموسع فعليًا فقط في بروتوكول FRI (Fast Reed-Solomon Interactive) والسيناريوهات الأخرى التي تتطلب مجموعات خطية عشوائية. لا تزال معظم العمليات الحسابية تتم في الحقول الأساسية، والتي عادةً ما تكون حقول modulo ppp أو qqq. بالإضافة إلى ذلك، يتم إجراء جميع البيانات المجزأة تقريبًا في الحقول الأساسية، لذلك يتم تجزئة أربعة بايت فقط لكل قيمة. يؤدي القيام بذلك إلى الاستفادة من كفاءة الحقول الصغيرة مع السماح باستخدام الحقول الأكبر عندما تكون هناك حاجة إلى تحسينات أمنية.
FRI عادي
عند إنشاء SNARK أو STARK، عادةً ما تكون الخطوة الأولى هي الحساب. هذا هو تحويل أي مشكلة حسابية إلى معادلة حيث تكون بعض المتغيرات والمعاملات متعددة الحدود. على وجه التحديد، ستبدو هذه المعادلة عادةً بالشكل P (X,Y,Z)=0P (X,Y,Z) = 0P (X,Y,Z)=0، حيث P هي كثيرة الحدود وZ هي معلمة معينة و يحتاج الحل إلى توفير قيم X وY. بمجرد حصولك على مثل هذه المعادلة، فإن حل تلك المعادلة يتوافق مع حل المشكلة الحسابية الأساسية.
لإثبات أن لديك حلًا، عليك أن تثبت أن القيم التي توصلت إليها هي في الواقع كثيرات حدود معقولة (وليست كسورًا، أو في بعض الحالات) تبدو الأماكن وكأنها كثيرة حدود واحدة، ولكنها متعددة الحدود مختلفة في مكان آخر، وما إلى ذلك)، وهذه كثيرات الحدود لها درجة قصوى معينة. للقيام بذلك، نستخدم تقنية التركيب الخطي العشوائي خطوة بخطوة:
لنفترض لديك تقييم لكثيرة الحدود A. وتريد إثبات أن درجتها أقل من 2^{20}
فكر في كثيرة الحدود B (x ^2) = A (x) + A (-x)، C (x^2) = \frac {A (x) - A (-x)}{x}
-
D عبارة عن مجموعة خطية عشوائية من B وC، أي D=B+rCD = B + rCD=B+rC، حيث r هو معامل عشوائي .
في الأساس، ما يحدث هو أن B يعزل المعاملات الزوجية A، ويعزل ? بالنظر إلى B وC، يمكنك استرداد كثيرة الحدود الأصلية A: A (x) = B (x^2) + xC (x^2). إذا كانت درجة A أقل بالفعل من 2^{20}، فإن درجتي B وC ستكونان درجة A ودرجة A ناقص 1 على التوالي. لأن الجمع بين الحدود الزوجية والفردية لا يزيد الدرجة. نظرًا لأن D عبارة عن مزيج خطي عشوائي من B وC، فيجب أن تكون درجة D أيضًا هي درجة A، مما يسمح لك باستخدام درجة D للتحقق من أن درجة A تلبي المتطلبات.
أولاً، تعمل FRI على تبسيط عملية التحقق من خلال تقليل مشكلة إثبات كثيرة الحدود بالدرجة d إلى مشكلة إثبات كثيرة الحدود بالدرجة d/2. يمكن تكرار هذه العملية عدة مرات، مما يؤدي إلى تبسيط المشكلة إلى النصف في كل مرة.
يعمل FRI عن طريق تكرار عملية التبسيط هذه. على سبيل المثال، إذا بدأت بإثبات أن درجة كثيرة الحدود هي d، فمن خلال سلسلة من الخطوات ستثبت في النهاية أن درجة كثيرة الحدود هي d/2. بعد كل تبسيط، تنخفض درجة كثير الحدود الناتج تدريجيًا. إذا لم يكن ناتج المرحلة من الدرجة متعددة الحدود المتوقعة، فستفشل جولة الاختبارات هذه. إذا حاول شخص ما دفع كثيرة حدود ليست من الدرجة d من خلال هذه التقنية، ففي الجولة الثانية من المخرجات، لن تلبي درجتها التوقعات باحتمال معين، وفي الجولة الثالثة سيكون من المرجح أن تكون غير متسقة، وأخيراً سوف يفشل الشيك. يمكن لهذا التصميم اكتشاف ورفض المدخلات التي لا تلبي المتطلبات بشكل فعال. من المرجح أن تجتاز مجموعة البيانات التحقق من صحة FRI إذا كانت تساوي متعددة الحدود من الدرجة d في معظم المواقع. ومع ذلك، من أجل إنشاء مجموعة البيانات هذه، يحتاج المهاجم إلى معرفة كثيرات الحدود الفعلية، لذلك حتى الدليل المعيب قليلاً يُظهر أن المُثبِّت قادر على إنشاء دليل "حقيقي".
دعونا نلقي نظرة فاحصة على ما يحدث هنا، والخصائص اللازمة لجعل كل هذا يعمل. في كل خطوة، نقوم بتقليل درجة كثير الحدود بمقدار النصف، وكذلك تقليل مجموعة النقاط (مجموعة النقاط التي نهتم بها) بمقدار النصف. الأول هو المفتاح لجعل بروتوكول FRI (Fast Reed-Solomon Interactive) يعمل بشكل صحيح. هذا الأخير يجعل الخوارزمية تعمل بسرعة كبيرة: بما أن حجم كل جولة يتم تقليله بمقدار النصف مقارنة بالجولة السابقة، فإن التكلفة الحسابية الإجمالية هي O (N) بدلاً من O (N*log (N)).
من أجل تحقيق التخفيض التدريجي للمجال، يتم استخدام تعيين اثنين لواحد، أي يتم تعيين كل نقطة إلى واحدة من نقطتين . يتيح لنا هذا التعيين تقليل حجم مجموعة البيانات إلى النصف. من المزايا المهمة لهذا التعيين الثنائي أنه قابل للتكرار. أي أنه عندما نطبق هذا التعيين، تظل مجموعة النتائج الناتجة تحتفظ بنفس الخصائص. لنفترض أننا بدأنا بمجموعة فرعية مضاعفة. هذه المجموعة الفرعية عبارة عن مجموعة S حيث يكون لكل عنصر x مضاعفاته 2x أيضًا في المجموعة. إذا قمت بتربيع المجموعة S (أي تعيين كل عنصر x في المجموعة إلى x^2)، فإن المجموعة الجديدة S^2 ستحتفظ بنفس الخصائص. تسمح لنا هذه العملية بمواصلة تقليل حجم مجموعة البيانات حتى تبقى قيمة واحدة فقط في النهاية. بينما يمكننا من الناحية النظرية تقليص مجموعة البيانات إلى قيمة واحدة فقط، إلا أننا من الناحية العملية نتوقف عادةً قبل الوصول إلى مجموعة أصغر.
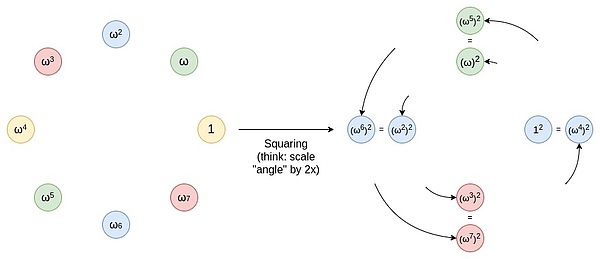
يمكنك اعتبار هذه العملية بمثابة عملية مد خط (على سبيل المثال، مقطع خطي أو قوس) على محيط الدائرة بحيث يدور مرتين حول الدائرة. على سبيل المثال، إذا كانت النقطة عند درجة x على المحيط، فسوف تنتقل إلى درجة 2x بعد هذه العملية. كل نقطة على الدائرة من 0 إلى 179 درجة لها نقطة مقابلة من 180 إلى 359 درجة، وهاتان النقطتان ستتطابقان. هذا يعني أنه عندما تقوم بتعيين نقطة من x درجة إلى 2x درجة، فإنها ستتزامن مع موضع عند x+180 درجة. يمكن تكرار هذه العملية. أي أنه يمكنك تطبيق عملية التعيين هذه عدة مرات، وفي كل مرة تقوم بتحريك النقاط الموجودة على المحيط إلى مواقعها الجديدة.
لكي تكون تقنية التعيين فعالة، يجب أن يكون لحجم المجموعة الفرعية المضاعفة الأصلية قوى كبيرة تبلغ 2 كعوامل. BabyBear هو نظام ذو معامل معين بحيث تحتوي مجموعته الفرعية المضاعفة القصوى على جميع القيم غير الصفرية، بحيث يكون حجم المجموعة الفرعية هو 2k−1 (حيث k هو عدد الأرقام في المعامل). المجموعات الفرعية بهذا الحجم مناسبة تمامًا للتقنية المذكورة أعلاه لأنها تسمح بتخفيض درجة كثير الحدود بكفاءة من خلال التطبيق المتكرر لعملية التعيين. في BabyBear، يمكنك تحديد مجموعة فرعية بحجم 2^k (أو مجرد استخدام المجموعة بأكملها)، ثم تطبيق طريقة FRI لتقليل درجة كثير الحدود تدريجيًا إلى 15، والتحقق من درجة كثير الحدود في النهاية. تستفيد هذه الطريقة من خصائص المعامل وحجم المجموعة الفرعية المضاعفة، مما يجعل عملية الحساب فعالة للغاية. Mersenne31 هو نظام آخر معامله هو بعض القيمة بحيث يكون حجم المجموعة الفرعية المضاعفة 2 ^ 31 - 1. في هذه الحالة، حجم المجموعة الفرعية المضاعفة له قوة 2 فقط كعامل، مما يسمح بتقسيمها على 2 مرة واحدة فقط. لم تعد المعالجة اللاحقة مناسبة للتقنيات المذكورة أعلاه، أي أنه من غير الممكن استخدام تحويل فورييه السريع (FFT) لتقليل درجة متعدد الحدود بكفاءة مثل BabyBear.
تعتبر نطاقات Mersenne31 مثالية لإجراء العمليات الحسابية على عمليات وحدة المعالجة المركزية/وحدة معالجة الرسومات 32 بت الحالية. بسبب خصائص المعامل (مثل 2^{31} - 1)، يمكن إكمال العديد من العمليات باستخدام عمليات البت الفعالة: إذا كانت نتيجة إضافة رقمين تتجاوز المعامل، فيمكن إزاحة النتيجة بواسطة عملية المعامل لتقليلها إلى النطاق المناسب. تعتبر عملية النزوح عملية فعالة للغاية. في عمليات الضرب، يتم استخدام تعليمات محددة لوحدة المعالجة المركزية (تسمى غالبًا تعليمات التحويل عالية الترتيب) لمعالجة النتيجة. يمكن لهذه التعليمات حساب الجزء عالي الترتيب من الضرب بكفاءة، وبالتالي تحسين كفاءة العملية. في مجال Mersenne31، تكون العمليات الحسابية أسرع بنحو 1.3 مرة من نطاق BabyBear نظرًا للخصائص الموضحة أعلاه. يوفر Mersenne31 كفاءة حسابية أكبر. إذا كان من الممكن تنفيذ FRI في مجال Mersenne31، فسيؤدي ذلك إلى تحسين الكفاءة الحسابية بشكل كبير وجعل تطبيقات FRI أكثر كفاءة.
ضع دائرة حول FRI
هذا هو الشيء الرائع في دائرة STARKs المعطاة لعدد أولي p، يمكن العثور على مجموعة سكانية ذات حجم p لها خصائص متشابهة من اثنين إلى واحد. يتكون هذا المجتمع من جميع النقاط التي تستوفي شروطًا معينة، على سبيل المثال، مجموعة النقاط حيث x^2 mod p تساوي قيمة معينة.
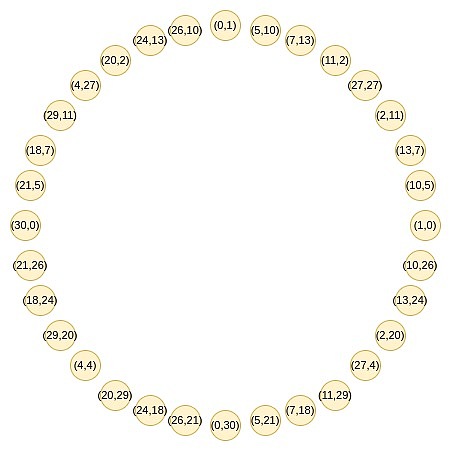
تتبع هذه النقاط نمطًا جمعيًا، والذي قد يبدو مألوفًا لك إذا كنت قد فعلت أي شيء متعلق بعلم المثلثات أو الضرب المعقد مؤخرًا.
(x_1, y_1) + (x_2, y_2) = (x_1x_2 - y_1y_2, x_1y_2 + x_2y_1)
< p style="text-align: left;">النموذج المضاعف هو:
2 * (x, y) = (2x^2 - 1, 2xy)
الآن، دعونا نركز على النقاط ذات الأرقام الفردية في الدائرة:
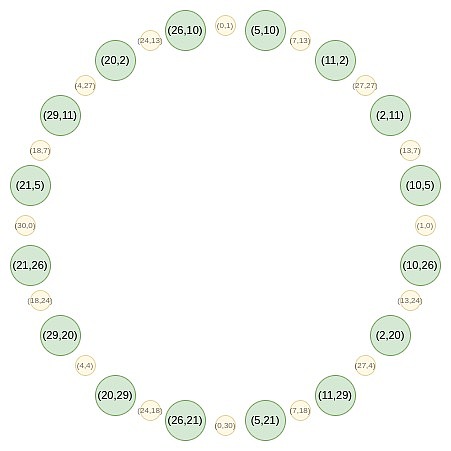
أولاً، نقوم بتقريب جميع النقاط إلى خط مستقيم. الصيغة المكافئة للصيغتين B (x²) وC (x²) التي نستخدمها في FRI العادية هي:
f_0 (x) = \frac { F (x,y) + F (x,-y)}{2}
بعد ذلك، يمكننا إجراء مجموعات خطية عشوائية للحصول على For P(x) أحادي البعد، يتم تعريف متعدد الحدود هذا عبر مجموعة فرعية من خطوط x:

بدءًا من الجولة الثانية، تغير التعيين:
f_0 (2x^2-1) = \frac {F (x) + F (-x)}{2}
يؤدي هذا التعيين في الواقع إلى تقليل حجم المجموعة المذكورة أعلاه بمقدار النصف في كل مرة، ما يحدث هنا هو أن كل x يمثل نقطتين بمعنى ما: (x, y) و (x, -y) . و(x → 2x^2 - 1) هي قاعدة مضاعفة النقاط أعلاه. لذلك، نقوم بتحويل إحداثيات x لنقطتين متقابلتين على الدائرة إلى إحداثيات x للنقطة المضروبة.
على سبيل المثال، إذا أخذنا القيمة الثانية على الدائرة من اليمين، 2، وقمنا بتطبيق التعيين 2 → 2 (2^2) - 1 = 7، النتيجة التي حصلنا عليها هي 7. وإذا رجعنا إلى الدائرة الأصلية، (2، 11) هي النقطة الثالثة من اليمين، فتضاعف حتى نحصل على النقطة السادسة من اليمين، وهي (7، 13).
كان من الممكن أن يتم ذلك في بعدين، لكن العمل في بعد واحد يجعل العملية أكثر كفاءة.
دائرة FFTs
الخوارزمية المرتبطة ارتباطًا وثيقًا بـ FRI هي FFT، والتي تحول التقييمات n من كثير الحدود بدرجة أقل من معاملات n إلى n لكثير الحدود. تشبه عملية FFT عملية FRI، باستثناء أنه بدلاً من إنشاء مجموعة خطية عشوائية من f_0 وf_1 في كل خطوة، يقوم FFT بشكل متكرر بإجراء تحويل FFT بنصف الحجم عليها وتحويل FFT (f_0). إخراج FFT (f_1) هو تستخدم كمعاملات زوجية، ويتم استخدام مخرجات FFT (f_1) كمعاملات فردية.
تدعم مجموعة الدوائر أيضًا FFT، والذي تم إنشاؤه بطريقة مشابهة لـ FRI. ومع ذلك، فإن الاختلاف الرئيسي هو أن Circle FFT (وCircle FRI) تتعامل مع كائنات ليست متعددة الحدود بشكل صارم. بدلا من ذلك، فهي ما يسمى رياضيا بمساحة ريمان-روش: في هذه الحالة، متعدد الحدود هو دائري معياري ( x^2 + y^2 - 1 = 0 ). أي أننا نعامل أي مضاعف لـ x^2 + y^2 - 1 على أنه صفر. هناك طريقة أخرى للتفكير في الأمر وهي: نحن نسمح فقط لـ y بالقوة: بمجرد ظهور مصطلح y^2، نستبدله بـ 1 - x^2 .
وهذا يعني أيضًا أن المعاملات الناتجة بواسطة Circle FFT ليست أحادية الحد مثل FRI العادي (على سبيل المثال، إذا كان إخراج FRI العادي هو [6, 2, 8, 3]، فنحن نعلم أن هذا يعني P (x) = 3x^3 + 8x^2 + 2x + 6). في المقابل، معاملات الدائرة FFT خاصة بأساس الدائرة FFT: {1, y, x, xy, 2x^2 - 1, 2x^2y - y, 2x^3 - x, 2x^3y - xy, 8x^4 - 8x^2 + 1...
الخبر السار هو أنه كمطور يمكنك تجاهل هذا تمامًا تقريبًا. ستاركس لا يطلب منك أبدًا معرفة المعاملات. بدلا من ذلك، يمكنك ببساطة تخزين كثير الحدود كمجموعة من القيم التي تم تقييمها على مجال معين. المكان الوحيد الذي تحتاج فيه إلى استخدام FFT هو إجراء امتداد منخفض الدرجة (على غرار مساحة Riemann-Roch): بالنظر إلى قيم N، قم بإنشاء قيم k*N، كلها على نفس متعدد الحدود. في هذه الحالة، يمكنك استخدام FFT لإنشاء المعاملات، وإلحاق أصفار (k-1) n بهذه المعاملات، ثم استخدام FFT العكسي للحصول على مجموعة أكبر من القيم المقدرة.
Circle FFT ليس نوع FFT الخاص الوحيد. تعد تحويلات التحويل السريع (FFTs) للمنحنى الإهليلجي أكثر قوة لأنها يمكن أن تعمل في أي مجال محدود (المجال الأولي، المجال الثنائي، وما إلى ذلك). ومع ذلك، فإن ECFFT أكثر تعقيدًا وأقل كفاءة، لذا بما أنه يمكننا استخدام Circle FFT على p = 2^{31}-1، فقد اخترنا استخدامه.
من هنا سنتعمق في بعض التفاصيل الأكثر غموضًا التي تجعل تطبيق Circle STARKs مختلفًا عن STARKs العادية.
القسمة
في بروتوكول STARK، العملية الشائعة هي إجراء حاصل قسمة محدد العملية، ويمكن اختيار هذه النقاط عمدا أو عشوائيا. على سبيل المثال، إذا كنت تريد إثبات أن P (x) = y، يمكنك المتابعة من خلال الخطوات التالية:
احسب حاصل القسمة: بالنظر إلى كثير الحدود P ( x) والثابت y، احسب حاصل القسمة Q ={P - y}/{X - x}، حيث X هي النقطة المحددة.
إثبات كثيرة الحدود: أثبت أن Q هي كثيرة الحدود وليست قيمة كسرية. وبهذه الطريقة، ثبت أن P(x)=y صحيحة.
بالإضافة إلى ذلك، في بروتوكول DEEP-FRI، يتم اختيار نقاط التقييم بشكل عشوائي لتقليل عدد فروع Merkle، وبالتالي تحسين أمان وكفاءة FRI بروتوكول.
عند التعامل مع بروتوكول STARK الخاص بمجموعة الدوائر، نظرًا لعدم وجود وظيفة خطية يمكنها المرور عبر نقطة واحدة، يجب استخدام تقنيات مختلفة لتحل محل التقليدية طريقة عمل الحاصل . يتطلب هذا غالبًا تصميم خوارزميات جديدة باستخدام الخصائص الهندسية الفريدة لمجموعات الدوائر.
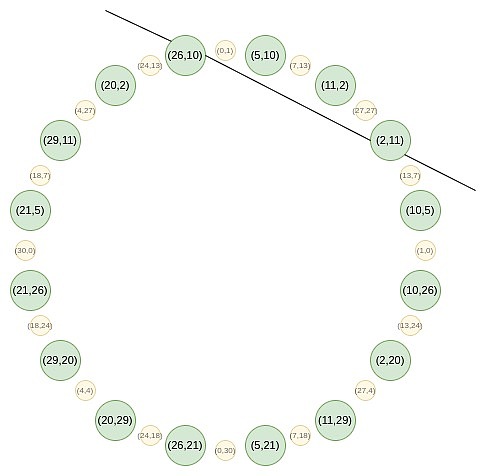
في المجموعة الدائرية، يمكنك إنشاء دالة ظل بحيث تقطع النقطة عند نقطة معينة (P_x، P_y)، ولكن هذه الدالة سيكون لها تعدد 2 خلال النقطة، وهذا هو أنه لكي تكون كثيرة الحدود من مضاعفات هذه الدالة الخطية، يجب أن تستوفي شروطًا أكثر صرامة من مجرد كونها صفرًا عند تلك النقطة. لذلك، لا يمكنك إثبات نتائج التقييم عند نقطة واحدة فقط. فكيف نتعامل مع هذا؟
علينا أن نقبل هذا التحدي ونثبت من خلال التقييم عند نقطتين، وبالتالي إضافة نقطة افتراضية لا نحتاج إلى التركيز عليها.

وظيفة الخط: ax + by + c. إذا حولتها إلى معادلة، وأجبرتها على أن تساوي 0، فقد تتعرف عليها كخط فيما يسمى بالشكل القياسي في رياضيات المدرسة الثانوية.
إذا كان لدينا كثيرة الحدود P تساوي y_1 عند x_1 وتساوي y_2 عند x_2، فيمكننا اختيار دالة الاستيفاء L التي تساوي y_1 عند x_1 يساوي y_1 ويساوي y_2 عند x_2. يمكن التعبير عن ذلك ببساطة كـ L = \frac {y_2 - y_1}{x_2 - x_1} \cdot (x - x_1) + y_1.
ثم نثبت أن P تساوي y_1 عند x_1 وتساوي y_2 عند x_2، عن طريق طرح L (بحيث يكون P - L عند النقطتين صفرًا) ، ثم قم بتقسيم L (أي الدالة الخطية بين x_2 - x_1) على L لإثبات أن حاصل القسمة Q هو متعدد الحدود.
اختفاء كثيرات الحدود
في STARK، تبدو المعادلة كثيرة الحدود التي تحاول إثباتها عادةً كما يلي: هي C (P (x)، P ({next}(x))) = Z (x) ⋅ H (x) حيث Z (x) هي كثيرة الحدود تساوي الصفر على نطاق التقييم الأصلي بأكمله. في STARK العادي، هذه الوظيفة هي x^n - 1. في STARK الدائرية، الوظيفة المقابلة هي:
Z_1 (x,y) = y
Z_2 (x,y) = x
Z_{n+1 } (x,y) = (2 * Z_n (x,y)^2) - 1
لاحظ أنه يمكنك اشتقاق كثيرة الحدود المتلاشية: في STARK العادي، يمكنك إعادة استخدام x → x^2، وفي STARK الدائري، يمكنك إعادة استخدام x → 2x^2 - 1. ومع ذلك، في الجولة الأولى، يمكنك القيام بذلك بشكل مختلف لأن الجولة الأولى مميزة.
ترتيب البت العكسي
في STARKs، لا يتم تقييم كثيرات الحدود عادةً بالشكل "الطبيعي" بطريقة ليست متسلسلة (على سبيل المثال P (1)، P (ω)، P (ω2)،...، P (ωn−1))، ولكن فيما أسميه ترتيب البت العكسي:
P (\omega^{\frac {3n}{8}})
إذا قمنا بتعيين n =16 ونركز فقط على قوى ω التي نقيمها، ثم تبدو القائمة كما يلي:
{0, 8, 4, 12, 2, 10, 6, 14, 1, 9, 5, 13, 3, 11, 7, 15
خاصية رئيسية لهذا الفرز هو أن القيم التي تم تجميعها معًا في وقت مبكر من عملية تقييم FRI ستكون متجاورة في الفرز، على سبيل المثال، ستكون الخطوة الأولى من FRI هي التجميع -x , ω^8 = -1, وهو ما يعني P (ω^i) ) و ( P (-ω^i) = P (ω^{i+8} ) \). كما نرى، هذه هي بالضبط الأزواج بجوار بعضها البعض. الخطوة الثانية لمجموعات FRI P (ω^i) و P (ω^{i+4}) و P (ω^{i+8}) و P (ω^{i+12}) . وهذا بالضبط ما نراه في مجموعات مكونة من أربعة أشخاص، وهكذا. يؤدي القيام بذلك إلى جعل FRI أكثر كفاءة في استخدام المساحة، لأنه يسمح لك بتوفير دليل Merkle للقيم المطوية معًا (أو، إذا قمت بطي جولات k في المرة الواحدة، جميع القيم 2^k).
في دائرة STARKs، يختلف هيكل الطي قليلًا: في الخطوة الأولى، نقارن (x, y) مع زوج (x, -y)؛ في الخطوة الثانية، قم بإقران x مع -x; وفي الخطوة التالية، قم بإقران p مع q ، واختيار p و q بحيث يكون Q^i ( p) = -Q ^i (q)، حيث Q^i هو تعيين يكرر x → 2x^2-1 i مرات. إذا فكرنا في النقاط من حيث موقعها على الدائرة، ففي كل خطوة يبدو هذا وكأن النقطة الأولى مقترنة بالنقطة الأخيرة، والنقطة الثانية مع النقطة الثانية إلى النقطة الأخيرة، وهكذا.
من أجل ضبط ترتيب البت العكسي ليعكس بنية الطي هذه، نحتاج إلى عكس كل بت باستثناء البت الأخير. نحتفظ بالجزء الأخير ونستخدمه لتحديد ما إذا كنا سنقلب الأجزاء الأخرى أم لا.
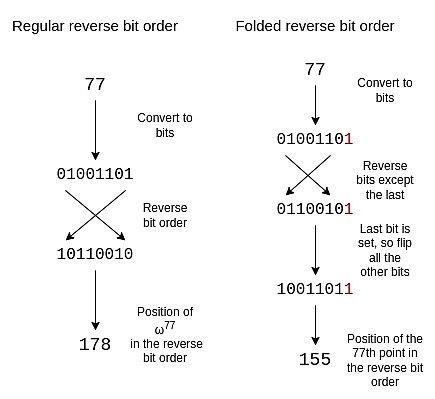
الترتيب العكسي للطية بحجم 16 هو كما يلي:
{0, 15, 8, 7 , 4, 11, 12, 3, 2, 13, 10, 5, 6, 9, 14, 1}
إذا لاحظت بالنسبة للدائرة في قسم واحد، ستجد أن النقاط 0 و 15 و 8 و 7 (عكس اتجاه عقارب الساعة من اليمين) هي (x، y)، (x، -y)، (-x، -y) و (- x، y)، وهو بالضبط ما نحتاجه.
الكفاءة
في دائرة STARKs (و STARKs 31 بت بشكل عام)، هذه البروتوكول فعال للغاية. تتضمن العملية الحسابية المثبتة في Circle STARK عادةً عدة أنواع من العمليات الحسابية:
1. الحساب الأصلي: يستخدم لمنطق الأعمال، مثل العد.
2. الحساب الأصلي: يستخدم في التشفير، مثل وظائف التجزئة مثل بوسيدون
3. معلمات البحث: طريقة حسابية عامة وفعالة تنفذ عمليات حسابية مختلفة من خلال قراءة القيم من الجدول.
المقياس الرئيسي للكفاءة هو ما إذا كنت تستخدم المساحة بأكملها في تتبع الحساب الخاص بك بشكل كامل للقيام بعمل مفيد، أو ما إذا كنت تترك الكثير من المساحة الحرة . في SNARKs للحقول الكبيرة، غالبًا ما يكون هناك الكثير من المساحة الحرة: غالبًا ما يتضمن منطق الأعمال وجداول البحث عمليات حسابية على أرقام صغيرة (تميل هذه الأرقام إلى أن تكون أقل من N، حيث N هو إجمالي عدد الخطوات في العملية الحسابية، لذلك في تدرب على أقل من 2^{25 })، ولكن لا يزال يتعين عليك دفع تكلفة استخدام حقل بحجم 2^{256} بت. حجم الحقل هنا هو 2^{31}، لذا فإن المساحة المهدرة ليست ضخمة. تستفيد التجزئات ذات التعقيد الحسابي المنخفض المصممة لـ SNARKs (مثل Poseidon) بشكل كامل من كل بت من كل رقم في التتبع في أي مجال.
يعد Binius حلاً أفضل من Circle STARKs لأنه يسمح لك بمزج الحقول ذات الأحجام المختلفة، مما يؤدي إلى تعبئة بتات أكثر كفاءة. يوفر Binius أيضًا خيار إجراء إضافات 32 بت دون تحميل جداول البحث. ومع ذلك، تأتي هذه المزايا على حساب (في رأيي) جعل المفهوم أكثر تعقيدًا، في حين أن Circle STARKs (و STARKs العادية المستندة إلى BabyBear) أبسط بكثير من الناحية النظرية.
الخلاصة: أفكاري حول دائرة STARKs
ضع دائرة حول STARKs للمطورين لم يعد الأمر كذلك معقدة من ستاركس. أثناء عملية التنفيذ، فإن المشكلات الثلاث المذكورة أعلاه هي في الأساس الاختلافات عن FRI التقليدية. على الرغم من أن الرياضيات وراء كثيرات الحدود التي تعمل عليها Circle FRI معقدة للغاية وتستغرق بعض الوقت لفهمها وتقديرها، إلا أن هذا التعقيد مخفي في الواقع كثيرًا بحيث لا يشعر به المطورون بشكل مباشر.
يمكن أن يكون فهم Circle FRI وCircle FFTs أيضًا طريقة لفهم تحويلات FFT الخاصة الأخرى: وأبرزها تحويلات FFT للمجال الثنائي، مثل Binius والسابقة LibSTARK يستخدم تحويل الأموال السريع (FFTs)، بالإضافة إلى بعض التركيبات الأكثر تعقيدًا، مثل تحويل الأموال السريع (FFTs) ذي المنحنى الإهليلجي. تستخدم هذه التحويلات تحويلات سريعة (FFTs) تعيينات قليلة إلى كثيرة ويمكن دمجها جيدًا مع عمليات نقطة المنحنى الإهليلجي.
بالدمج مع Mersenne31 وBabyBear وتقنيات المجال الثنائي مثل Binius، نشعر أننا نقترب من حدود كفاءة الطبقة الأساسية لـ STARKs. في هذه المرحلة، أتوقع أن يركز اتجاه تحسين STARK على النقاط التالية:
حساب وظائف التجزئة والتوقيعات لزيادة الكفاءة إلى أقصى حد: تحسين أساسيات التشفير الأساسية مثل وظائف التجزئة والتوقيعات الرقمية في أشكالها الأكثر كفاءة حتى تتمكن من تحقيق أفضل أداء عند استخدامها في إثباتات STARK. وهذا يعني تحسينات خاصة لهذه البدائيات لتقليل الجهد الحسابي وزيادة الكفاءة.
البناء العودي لتمكين المزيد من التوازي: يشير البناء العودي إلى تطبيق عملية إثبات STARK بشكل متكرر على مستويات مختلفة، وبالتالي زيادة قدرات المعالجة المتوازية. وبهذه الطريقة، يمكن استخدام موارد الحوسبة بشكل أكثر كفاءة ويمكن تسريع عملية الإثبات.
آلة افتراضية حسابية لتحسين تجربة المطور: تتيح المعالجة الحسابية للأجهزة الافتراضية للمطورين إنشاء مهام الحوسبة وتشغيلها بشكل أكثر كفاءة وبساطة. يتضمن ذلك تحسين الجهاز الظاهري لاستخدامه في إثباتات STARK وتحسين تجربة المطور عند إنشاء واختبار العقود الذكية أو مهام الحوسبة الأخرى.
 Alex
Alex
 Alex
Alex Miyuki
Miyuki Alex
Alex Miyuki
Miyuki Weiliang
Weiliang Alex
Alex Catherine
Catherine Miyuki
Miyuki Joy
Joy Kikyo
Kikyo