ヴィタリック:どのようにイーサにアラインすべきか
「エーテルアライメント」には、価値観のアライメント、技術的アライメント、経済的アライメントなどが含まれる。
 JinseFinance
JinseFinance
コンパイル:ケイト、マーズファイナンス
過去2年間で、STARKは非常に複雑なステートメント(例えば、イーサネットブロックが有効であることを証明する)の検証可能な暗号証明を効率的に実行できる、重要かつかけがえのない技術として登場しました。イーサネットブロックが有効であることを証明するなど)。
その主な理由の1つはフィールドサイズです。楕円曲線ベースのSNARKでは、十分に安全であるためには256ビットの整数で作業する必要がありますが、STARKではより小さいフィールドサイズで作業できるため、はるかに効率的です。まずGoldilocksフィールド(64ビット整数)、次にMersenne31とBabyBear(どちらも31ビット)。これらの効率化の結果、Goldilocksを使用したPlonky2は、幅広い計算を証明する際に、以前のものより数百倍速くなりました。
自然な疑問は、この傾向を論理的な結論に導き、0と1を直接操作することでより高速に動作する証明システムを構築できないかということです。これはまさにBiniusが試みたことであり、3年前のSNARKやSTARKとは根本的に異なる数多くの数学的トリックを使用している。この記事では、なぜ小さな場が証明生成をより効率的にするのか、なぜバイナリ場が他に類を見ないほど強力なのか、そしてバイナリ場上の証明を非常に効率的にするためにBiniusが使っているトリックについて説明する。

△ ビニウス この記事の最後にあります。この図のすべての部分を理解できるはずだ。
復習:有限体
暗号証明システムの重要な仕事の1つは、数を小さく保ちながら大量のデータを操作することです。小さい。大きなプログラムに関する記述を、いくつかの数字を含む数式に圧縮することができても、その数字が元のプログラムと同じくらい大きければ、どこにもたどり着けません。
数を小さく保ちながら複雑な算術を行うために、暗号技術者はモジュラー算術をよく使います。演算子%は「余りを取る」ことを意味する:15%7=1、53%10=3など(答えは常に負でないことに注意)。(答えは常に非負なので、例えば-1%10=9)
余りを取る。align: left;">モジュロ演算は、おそらく時間の足し算や引き算の文脈で見たことがあるでしょう(例えば、9時4分過ぎは何時ですか?)しかしここでは、単に足したり引いたりするだけでなく、掛けたり割ったり、指数を取ったりすることもできます。
私たちは再定義します:
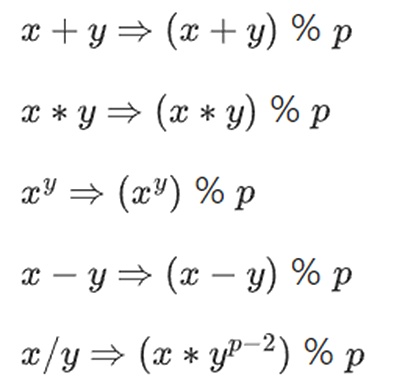
5+3=1 (8%7=1 なので)
1-3=5 (-2%7=5 なので)
2*5=3
3/5=2
この構造のより一般的な用語は有限体である。有限体とは、通常の算術法則に従った数学的構造であるが、その中で取り得る値の数は有限であり、各値は一定の大きさで表すことができる。
モジュラー算術(または素数体)は有限体の最も一般的なタイプですが、もう一つのタイプとして拡張体があります。拡張体というのはすでに見たことがあるかもしれない。3i+2)*(2i+4)=6i*i+12i+4i+8=16i+2である。同じように素数体も拡張することができる。より小さな場を扱うようになると、素数体の拡張は安全性を保つためにますます重要になり、2進数体(ビニウスはこれを用いている)は実用的であるために拡張に完全に依存している。
復習:算術化
SNARKとSTARK コンピュータプログラムを証明する方法は算術である。を多項式を含む数式に変換する。方程式の有効な解は、プログラムの有効な実行に対応する。
簡単な例として、私が100番目のフィボナッチ数を計算したとします。F(0)=F(1)=1、F(2)=2、F(3)=3、F(4)=5......というように、100ステップのフィボナッチ級数を符号化する多項式Fを作った。私が証明しなければならない条件は、x={0,1...98}の全範囲にわたってF(x+2)=F(x)+F(x+1)であることである。
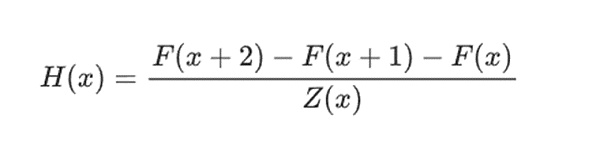
ここでZ(x) = (x-0) * (x-1) * ...(x-98)...Fがあり、Hがこの方程式を満たすことを提供できれば、Fはその範囲でF(x+2)-F(x+1)-F(x)を満たさなければならない。さらにFを満たすことを検証すると、F(0)=F(1)=1となり、F(100)は実際には100番目のフィボナッチ数でなければならない。
より複雑なことを証明したいのであれば、「単純な」関係式F(x+2) = F(x) + F(x+1)を、基本的には「F(x+1)はVMを状態F(x)で初期化したときの出力である」という、より複雑な式に置き換えて、計算ステップを実行します。また、より多くのステップに対応するために、100という数字をより大きな数字、例えば100000000に置き換えることもできます。
SNARKとSTARKはすべて、個々の値間の多数の関係を表現するために、多項式(場合によってはベクトルや行列)上の簡単な方程式を使用するという考えに基づいています。例えばPLONKはそうではないし、R1CSもそうである。しかし、最も効率的なチェックの多くは、同じチェック(または同じいくつかのチェック)を複数回実行することで、オーバーヘッドを最小限に抑えることが容易になるため、そうしています。
Plonky2:256ビットのSNARKとSTARKから64ビットへ......。STARKのみ
5年前からのゼロ知識証明のさまざまなタイプの妥当な要約は次のとおりです。技術的には、STARKはSNARKの一種ですが、実際には、楕円曲線ベースの変形を指すのに「SNARK」を使い、ハッシュベースの構築を指すのに「STARK」を使うのが一般的です。 SNARKは非常に小さいので、非常に素早く検証できます!STARKは大きいですが、信頼できるセットアップを必要とせず、量子耐性があります。

△ STARKは、データを多項式として扱うことで動作します。多項式としてデータを扱い、その多項式の計算を行い、拡張されたデータのメルクル根を「多項式のコミットメント」として使用します。
ここで重要な歴史は、楕円曲線ベースのSNARKが最初に広く使用されたことです。FRIのおかげでSTARKが十分に効率的になったのは2018年頃までで、その頃にはZcashは1年以上稼働していました。楕円曲線ベースのSNARKには1つ重要な制限があります。楕円曲線ベースのSNARKを使いたい場合、その方程式の演算は楕円曲線上の点の数のモジュラスを使って行わなければなりません。例えば、bn128曲線は21888242871839275222246405745257275088548364400416034343698204186575808495617です。 しかし、実際の計算には小さな数字が使われます。好きな言語で「楕円曲線」を「本当の」プログラムと見なした場合、それが使用するもののほとんどは、カウンタ、forループのインデックス、プログラム内の位置、TrueまたはFalseを表す個々のビットなど、ほとんど常に数桁の長さしかないものです。
たとえ「生の」データが「小さな」数字で構成されていたとしても、証明プロセスでは商、展開、ランダムな線形結合、その他のデータ変換を計算する必要があり、その結果、平均してフィールドの全サイズと同じかそれ以上の大きさのオブジェクトが生成されます。n個の小さな値に対する計算を正当化するために、n個のはるかに大きな値に対してより多くの計算を実行しなければならないのです。当初、STARKは256ビットのフィールドを使用するというSNARKの習慣を受け継いでいたため、同じ非効率性に悩まされていました。

△ いくつかの多項式値Reed-Solomon拡張。ソロモン拡張。元の値は小さいが、余分な値はフィールドのサイズいっぱいに拡張される(この場合、2の31乗-1)
2022年、Plonky2がリリースされた。 Plonky2の主な革新は、小さな素数をモジュロした演算である:2の64乗+1。- 2 の32乗 + 1 = 18446744067414584321 これで、各加算や乗算は常にCPUの数命令で実行でき、すべてのデータをまとめてハッシュ化すると、以前より4倍速くなる。SNARKを使おうとすると、このような小さな楕円曲線では楕円曲線が安全でなくなってしまいます。
安全であるためには、Plonky2も拡張フィールドを導入する必要があります。H(x)*Z(x)がF(x+2)-F(x+1)-F(x)に等しいかどうかをチェックしたい場合、ランダムに座標rを選び、H(r)、Z(r)、F(r)、F(r+1)、F(r+2)を示す証明を開くための多項式コミットメントを提供し、H(r)*Z(r)がF(r+2) - F(r+1) - F(r)に等しいことを検証する。もし攻撃者が前もって座標を推測することができれば、攻撃者は証明システムを詐称することができる--これが証明システムがランダムでなければならない理由である。しかしこれは、攻撃者がランダムな推測ができないように、座標が十分に大きな集合からサンプリングされなければならないことも意味する。これは明らかに、2の256乗に近いモジュラスの場合に当てはまります。しかし、2の64乗-2乗-32乗+1乗のモジュラスでは、まだそこまでには至っておらず、2の31乗-1乗まで下がると、確かにそうではない。運が良くなるまで20億回証明を偽造しようとすることは、間違いなく攻撃者の能力の範囲内です。
これを阻止するために、拡張フィールドからrをサンプリングしてみましょう。例えば、yの3乗=5と定義し、1、y、yの2乗の組み合わせを取ることができます。こうすると、座標の総数は2の93乗程度に増える。証明者が計算する多項式のほとんどはこの拡張領域には入らず、2 - 1の31乗の整数を取るだけなので、小さな領域を使うことによる効率はそのまま得られる。しかし、ランダム・ポイント・チェックとFRIの計算は、必要なセキュリティを得るために、この大きな領域に踏み込みます。
小さな素数から2進数まで
コンピュータは、より大きな数を0と1のシーケンスとして表現し、それらのビットの上に「回路」を構築することによって、算術演算を実行します。コンピュータは、より大きな数を0と1のシーケンスとして表現し、これらのビットの周囲に「回路」を構築して足し算や掛け算などの演算を計算することで算術演算を行う。コンピュータは16ビット、32ビット、64ビットの整数に最適化されている。例えば、2の64乗-2の32乗+1や2の31乗-1が選ばれたのは、これらの境界に適合しているからだけでなく、これらの境界によく適合しているからでもある。通常の32ビット乗算を実行し、出力をビットシフトして数カ所でコピーすることで、2の64乗-2の32乗+1のモジュロ乗算を実行することが可能である。
しかし、より良いアプローチは2進数で直接計算することです。もし足し算が「単に」等号になったり、あるビットから次のビットへの1 + 1の足し算のオーバーフローを「持ち運ぶ」ことを気にせずに済むとしたらどうでしょう?同じように乗算もより並列化できるとしたら?これらの利点はすべて、1ビットで真偽値を表現できることに基づいています。
直接2進計算のこれらの利点を得ることは、まさにBiniusがやろうとしていることであり、BiniusチームはzkSummitの講演で効率性の向上を実証しました:
ほぼ同じ「サイズ」であるにもかかわらず、32ビットのバイナリフィールド演算は、31ビットのメルセンヌフィールド演算よりも5倍少ない計算リソースを必要とします。
単項式から超立方体まで
この推論を信じ、すべてをビット(0と1)で行いたいとします。10億ビットを多項式として表現するにはどうすればよいでしょうか。
ここで私たちは2つの現実的な問題に直面します:
多数の値を表す多項式では、これらの値は多項式の評価中にアクセス可能である必要があります。上記のフィボナッチの例では、F(0)、F(1)・・・F(100)、もっと大きな計算では、指数は数百万になるでしょう。我々が使用するフィールドは、そのサイズまでの数値を含む必要がある。
(すべてのSTARKのように)Merkleツリーで提出する値は、Reed-Solomonでエンコードする必要があることを証明する。また、冗長性を利用することで、悪意のある証明者が計算中に値を偽って不正を行うことを防ぎます。100万の値を800万に拡張するには、多項式を計算するために800万の異なる点が必要になります。
Biniusの重要なアイデアの1つは、これら2つの問題を別々に解決することであり、同じデータを2つの異なる方法で表現することで解決することです。まず、多項式そのものである。
楕円曲線に基づくSNARK、2019時代のSTARK、Plonky2などのシステムは、通常1変数の多項式:F(x)を扱う。一方、BiniusはSpartanプロトコルからヒントを得て、F(x1,x2,...xk)という多変数の多項式を使用します。事実上、計算の軌跡全体を計算「超立方体」上に表し、各xiは0か1のいずれかである。例えば、フィボナッチ級数を表したい場合、それでもそれらを表すのに十分な大きさのフィールドを使えば、最初の16個を次のように想像できる:

つまり、F(0,0,0,0)は1であるべきで、F(1,0,0,0)も1であるべきで、F(0,1,0,0)は2である。F(1,1,1,1)=987まで続く。このような計算の超立方体が与えられると、これらの計算を生成する多変量線形(各変数は次数1)の多項式が存在する。つまり、この値の集合を多項式の表現と考えることができる。
この例はもちろん説明のためのものです。実際には、超立方体にすることの要点は、個々のビットで作業できるようにすることです。フィボナッチ数を計算する「ビニウス・ネイティブ」な方法は、高次元の立方体を使用し、各グループで16ビットを使用して1つの桁を格納することです。これにはビットの上に整数を加える工夫が必要だが、ビニウスにとってはそれほど難しいことではない。
さて、打ち切りについて見てみましょう。これはSTARKがどのように機能するかということです:n個の値を取り、リードソロモンでより多くの値(通常は8n個、多くの場合は2n個から32n個の間)に展開します。チェックを行う。超立方体は各次元とも長さが2なので、それを直接展開するのは非現実的だ:16個の値からメルクル分岐をサンプリングするには十分な「スペース」がない。ではどうするか?超立方体を正方形と仮定してみましょう!
Simple Binius - An Example
プロトコルのpython実装については、以下のリンクをブラウザにコピーしてください。https://github.com/ethereum/research/blob/master/binius/simple_binius.py
例を見てみましょう。をフィールドとして使用してみましょう(実際の実装では、バイナリのフィールド要素が使用されます)。
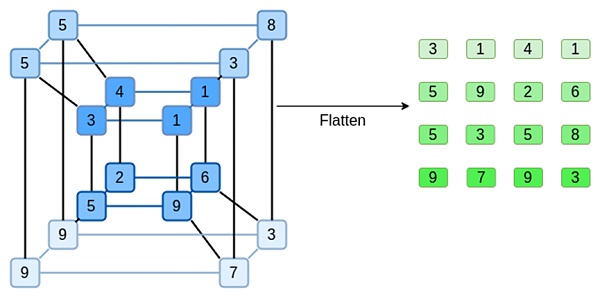
ここで、正方形をリード・ソロモンで拡張します。つまり、各行をx = {0,1,2,3}の値を持つ3次の多項式として扱い、x = {4,5,6,7}の値を持つ同じ多項式を扱います:

数字が急速に拡大することに注意してください!そのため、実際の実装では、通常の整数ではなく、常に有限体を使っています。例えば、11モジュロの整数を使うと、最初の行の展開は[3,10,0,6]となります。
自分で展開を試して数字を確かめたい場合は、ここで私の簡単なリードソロモン展開コードを使うことができます。
次に、この拡張を列として扱い、列のメルクルツリーを作成します。メルクルツリーのルートは私たちのコミットメントです。
ここで、証明者がいつかこの多項式の計算を証明したいと仮定しましょう。この多項式r={r0,r1,r2,r3}の計算を証明したいとします。Biniusには、他の多項式コミットメントスキームよりも弱いニュアンスがあります。つまり、証明者はメルクル根にコミットする前にsを知らないか、推測することができません(言い換えれば、rはメルクル根に依存する擬似乱数値でなければなりません)。このため、このスキームは「データベース検索」には役に立たない(例えば、"OK、あなたは私にメルクル根を与えた、今度は私にP(0,0,1,0)を証明してくれ!)!").
しかし、私たちが実際に使うゼロ知識証明プロトコルは、通常「データベース検索」を必要としません。したがって、この制限は私たちの目的に合っています。
r={1,2,3,4}を選んだとします(この時点で多項式は-137と計算されます。)さて、証明に移ります。最初の部分{1,2}は行内の列の線形結合を表し、2番目の部分{3,4}は行の線形結合を表します。
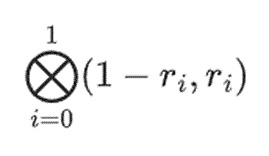
列の部分については「テンソル積」を計算します。

これは次のことを意味する。値のすべての可能な製品のリスト。行の場合は次のようになる:
[(1-r2)*(1-r3), (1-r3), (1-r2)*r3, r2*r3]
r={1,2,3,4}を使う(つまりr2=3、r3=4)。3 and r3=4):
[(1-3)*(1-4), 3*(1-4), (1-3)*4,3*4] = [6, -9 -8 -12]
ここで、既存の線形結合の線を用いて新しい線を計算する。つまり、
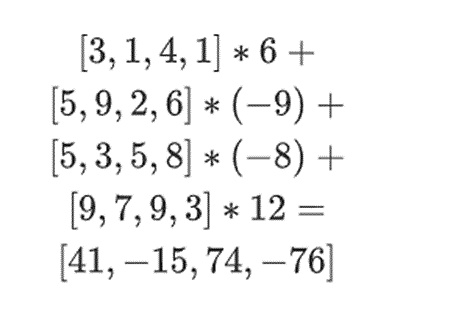
新しい「行」tを計算するために、既存の線形結合を採用して新しい行を計算します。:left;">ここで起こっていることは部分和と考えることができる。完全なテンソル積にすべての値の完全なベクトルを掛けると、P(1,2,3,4) = -137という計算になります。ここでは、評価された座標の半分だけを使って部分テンソル積を掛け、N値の格子をルートN値の行に減らします。この行を他の人が利用できるようにすれば、評価座標の残りの半分のテンソル積を使って残りの計算をすることができる。
証明者は検証者に、以下の新しい行を提供します: t とランダムにサンプリングされた列に対するメルクル証明。この例では、証明者に最後の列のみを提供させる。現実には、証明者は十分なセキュリティを達成するために数十の列を提供する必要がある。
ここで、リードソロモンコードの線形性を利用します。私たちが利用する重要な特性は、リード・ソロモン拡張の線形結合をとると、リード・ソロモン拡張の線形結合と同じ結果が得られるということです。この「逐次的な独立性」は通常、両方の演算が線形である場合に発生します。
検証者はまさにそれを行いました。彼らはtを計算し、以前に証明者が計算したのと同じ列(ただし、証明者が提供した列のみ)の線形結合を計算し、2つの処理が同じ答えを与えることを検証します。
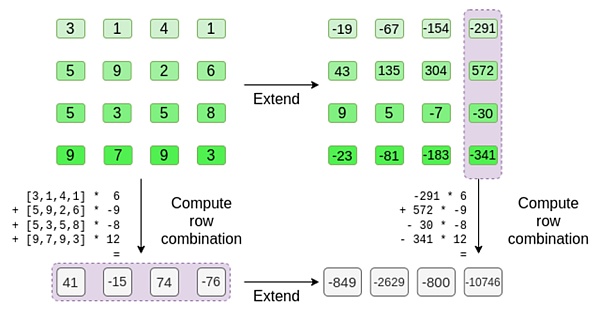
この例では、同じ線形結合([6,-9;])を計算するのは拡張tです。これは、Merkleのルートが「誠実に」(あるいは少なくとも「十分に近く」)構築され、tと一致することを証明している。
しかし、検証者がチェックしなければならないことがもう一つあります:多項式{r0...r3}の和をチェックすることです。これまでのところ、検証者のどのステップも、実際には証明者が主張する値に依存していない。これを確認する方法を説明しよう。
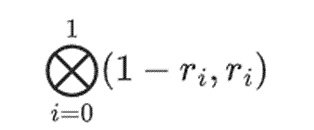
私たちの例では、r={1,2,3,4}で選択列の半分が{1,2}である)、これは次のように等しい:
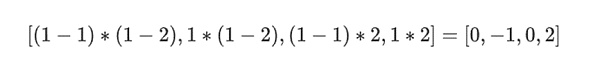
ここで、この線形結合tを取ります:
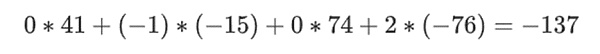
これは多項式を直接取るのと同じ結果です。
上記は、「単純な」Biniusプロトコルの完全な記述に非常に近いものです。例えば、データは行と列に分割されるので、フィールドは半分の大きさで済みます。しかし、これではバイナリ計算の利点をフルに発揮することはできない。そのためには、完全なビニウス・プロトコルが必要だ。しかしその前に、バイナリー・フィールドを深く見てみよう。
2進数場
可能な最小の場は算術モジュロ2であり、その加算表と乗算表を書くことができるほど小さいです:
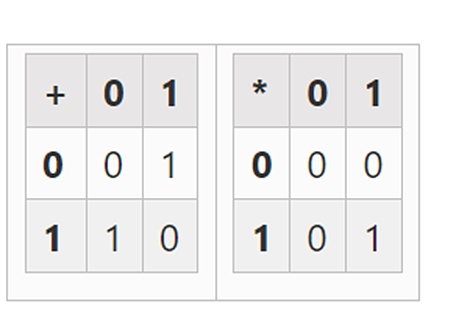
展開によってより大きな2進数を得ることができます。2)から始めてxを定義し、xの2乗=x+1とすると、次の加算表と乗算表が得られます:
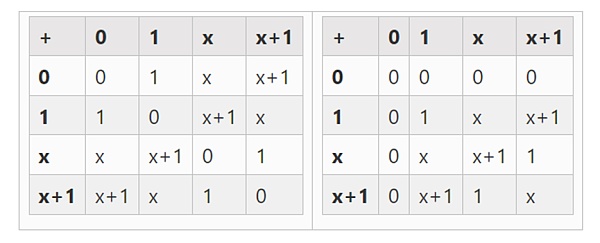
この構成を繰り返すことで、2進数を任意の大きさに拡張できることがわかった。実数上の複素数では、新しい要素を追加することはできても、それ以上の要素を追加することはできませんが(四元数は存在しますが、abはbaと等しくないなど、数学的に奇妙です)、有限体では、永遠に新しい拡張を追加することができます。具体的には、以下のように要素を定義します:
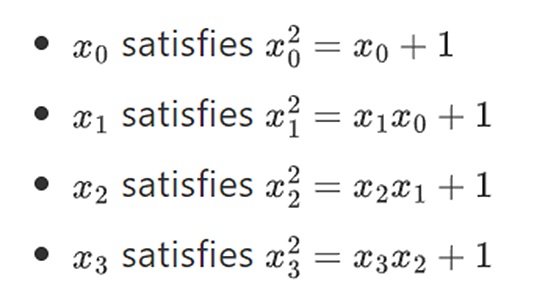
。待てよ......。これはタワー構造と呼ばれることが多いが、その理由は、増築を重ねるごとにタワーに新しい層が加わっていくように見えるからだ。これは任意の大きさのバイナリフィールドを構築する唯一の方法ではないが、ビニウスが利用するいくつかのユニークな利点がある。
これらの数をビットのリストとして表すことができる。最初のビットは1の倍数を表し、2番目のビットはx0の倍数を表し、それ以降のビットは次のx1の倍数を表します:x1、x1*x0、x2、x2*x0、など。
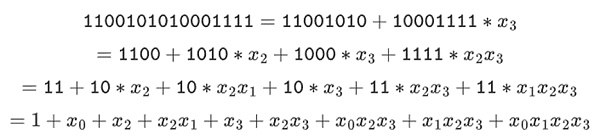
このエンコーディングは、それを分解することができるので素晴らしいです。これは比較的珍しい表現だが、私は2進数のフィールド要素を整数として表現するのが好きで、より効率的なビットを右側にしたビット表現を使っている。つまり、1=1、x0=01=2、1+x0=11=3、1+x0+x2=11001000=19、といった具合だ。この式では、61779です。
2進フィールドでの足し算は、単なるiso orです(ちなみに引き算もそうです)。
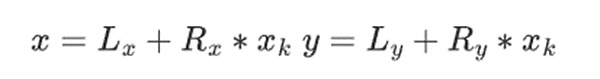
次に、掛け算を分割します。"text-align:center">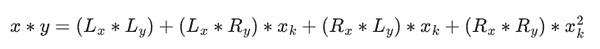
最後の部分だけは、単純化ルールを適用しなければならないので、ちょっと厄介です。カラツバアルゴリズムや高速フーリエ変換のような、乗算を行うより効率的な方法がありますが、興味のある読者が理解するための練習として残しておきます。
2進フィールドにおける除算は、乗算と反転を組み合わせて行われる。"単純だが遅い "反転法は、一般化されたフェルマーの小定理の応用である。より複雑だが効率的な反転アルゴリズムもある。ここのコードを使って、2進数フィールドの足し算、掛け算、割り算で遊ぶことができます。
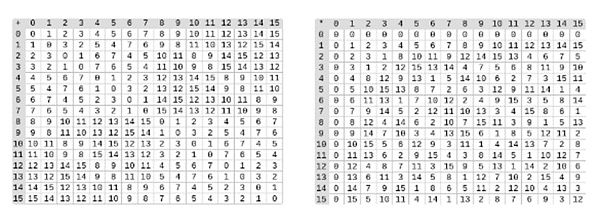
△ 左:4ビットの2進数フィールド要素(すなわち、次の要素だけからなるフィールド)。1,x0,x1,x0x1)の加算表。右:4つの2進フィールド要素の乗算表。
このタイプの2進フィールドの美点は、「通常の」整数とモジュロ演算の良いところを組み合わせていることである。通常の整数のように、バイナリフィールドの要素は束縛されない。しかしモジュロ演算のように、あるサイズ制限内の値に対して演算を行うと、すべての結果も同じ範囲内に収まります。例えば、42の累乗を取ると、次のようになります:

。正整数やモジュロ算のように、a*b = b*a、a*(b+c) = a*b + a*c、さらにいくつかの奇妙な新しいものなど、通常の数学的法則に従います。
最後に、バイナリフィールドはビットの扱いを簡単にします。2のk乗に収まる数で計算を行う場合、すべての出力も2のk乗ビットに収まります。EtherのEIP-4844では、ブロブの個々の "ブロック "は52435875175126190479447740508185965837690552500527637822603658699938581184513の数値モジュロでなければならない。各要素が2の248乗より小さい値を格納することを保証するために、アプリケーション層で追加のチェックを行います。
これはまた、バイナリフィールド演算が、CPUと理論的に最適なFPGAおよびASIC設計の両方のコンピュータ上で超高速であることを意味します。
これらのことは、上でリード・ソロモン・エンコーディングが行ったことを、例で見てきたように整数の「爆発」を完全に回避する方法で、しかもコンピュータが得意とする非常に「ネイティブ」な方法で行えることを意味します。バイナリフィールドの「分割」特性、つまり1100101010001111=11001010+10001111*x3とし、それを必要に応じて分割する方法も、多くの柔軟性を実現する上で非常に重要です。
完全なBinius
プロトコルのpython実装については、以下のリンクをコピーしてブラウザで確認してください: https://github.com/ethereum/research/blob/master/binius/packed_binius.py
さて、私たちは「単純なビニウス」を調整する「完全なビニウス」に行くことができます。このプロトコルは、ビット行列の異なる見方を行ったり来たりするので、理解するのが難しい。確かに、暗号プロトコルを理解するのに通常かかる時間よりも、理解するのに時間がかかった。しかし、一度バイナリフィールドを理解すれば、ビニウスが依拠する「より難しい数学」は存在しないという良いニュースがある。
これは、より深い代数幾何学のウサギの穴がある楕円曲線ペアリングではありません。
もう一度チャート全体を見てみましょう。

ここまでで、ほとんどの構成要素に慣れたはずだ。超立方体をグリッドに「平坦化」するアイデア、評価された点のテンソル積として行結合と列結合を計算するアイデア、「リード-ソロモン拡張と行結合の計算」と「行結合の計算とリード-ソロモン拡張」の間の等価性をテストするアイデアは、すべて単純な Binius で実装されています。
「完全なビニウス」では何が新しくなったのか?
ハイパーキューブと正方形の個々の値はビット(0または1)でなければなりません。
展開処理は、ビットを列にグループ化し、それらがより大きなフィールド要素であると一時的に仮定することで、ビットをより多くのビットに展開します
行結合ステップの後
この2つのケースを順番に説明します。まず、新しい拡張手順です。リードソロモン符号には基本的な制限があり、nをk*nまで拡張したい場合、座標として使用できるk*n個の異なる値を持つフィールドで作業する必要があります。F2(別名ビット)ではそれができない。そこで私たちが行うのは、隣り合うF2の要素を「パック」して、より大きな値を形成することです。この例では、一度に2ビットを{0, 1, 2, 3}の要素に詰め込んでいます。本当の」証明では、一度に16ビットを返すかもしれない。

ここで疑問が生じます。私たちはビットをより大きな値に結合し、その上でリードソロモン拡張を行う方法を知っていますが、より大きな値のペアに対して同じことを行うにはどうすればよいのでしょうか?
ビニウスのトリックは、それをビット単位で行うことです。各値の個々のビットを調べ(例えば、「11」とラベル付けしたもの、つまり[1,1,0,1])、それを行単位で展開します。展開処理はオブジェクトに対して行われる。つまり、各要素に対して1行ずつ展開処理を行い、x0行、"x1 "行、x0x1行と展開していきます(おもちゃの例ではここで止まっていますが、実際の実装では128行になります(最後はx6*...*x0になります))
レビュー
超立方体のビットを取り出し、グリッドに変換します。Reed-Solomonで拡張された行です。
次に、各列のビットの行の組み合わせを取り、各行のビット列を出力として得ます(4x4より大きい正方形では、かなり小さくなります)。
最後に、出力を行列、そのビットを行と考えます。
これはなぜでしょうか?通常の」数学では、ビットごとに数値をスライスし始めると、(通常は)どのような順序で線形演算を行っても同じ結果を得ることができなくなります。
例えば、345という数字から始めて、それを8倍し、さらに3倍すると、8280になり、この2つの操作を逆にすると、8280にもなります。 しかし、この2つのステップの間に「ビットごとのスライス」操作を入れると、破綻します。3回行うと、次のようになります:
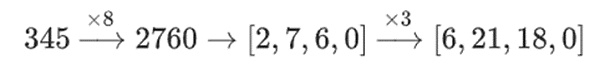
しかし、3回行ってから8回行うと、次のようになります:
しかし、3回行ってから8回行うと、次のようになります
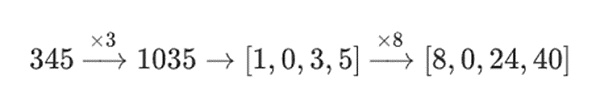
しかし、タワーで構築されたバイナリフィールドでは、バイナリフィールドを構築するために、このようなアプローチを使用することはできません。構造でバイナリーフィールドを構築する場合、このアプローチは機能する。大きな値に小さな値を掛けた場合、各線分で起こったことは各線分に留まるからだ。1100101010001111に11を掛けると、これは1100101010001111の最初の分解と同じになる

次に各成分を別々に同じ11倍する。
それらをまとめる
一般的に、ゼロ知識証明システムは、基礎となる評価に関する記述を示しながら、多項式に関する記述を行うことで機能します。フィボナッチの例で見たように、F(X+2)-F(X+1)-F(X)=Z(X)*H(X)でありながら、フィボナッチの計算のすべてのステップをチェックする。ランダムな点での値を証明することで、多項式に関する記述をチェックする。このランダムな点でのチェックは、多項式全体のチェックを意味します:多項式の式が一致しない場合、特定のランダムな座標で一致する可能性は非常に低いです。
実際には、非効率の主な理由の1つは、実際のプログラムで扱う数値のほとんどが小さいことです。しかし、Reed-Solomonエンコーディングを使ってデータを「拡張」し、Merkle証明ベースのチェックを安全にするために必要な冗長性を持たせると、元の値が小さくても、ほとんどの「余分な」値がフィールドのサイズ全体を占めてしまうことになります。
これを回避するために、私たちはフィールドをできるだけ小さくしたいと考え、Plonky2では256ビット数から64ビット数へ、そしてPlonky3ではさらに31ビット数へと縮小しました。しかし、これでも最適ではない。バイナリフィールドを使用することで、1ビットを扱うことができます。これにより、エンコーディングが「密」になります。実際の基礎となるデータがnビットであれば、エンコーディングはnビットとなり、拡張は8 * nビットとなり、追加のオーバーヘッドはありません。
さて、このグラフを3回目に見てみましょう。p>
ビニウスでは、多線形多項式:超立方体P(x0,x1,...xk)にコミットしており、個々の評価であるP(0,0,0,0)、P(0,0,0,1)からP(1,1,1,1)までが、我々が気にかけるデータを保持しているデータ。ある点での計算を正当化するために、同じデータを正方形として「再解釈」する。次に、リード・ソロモン符号化を使って各行を展開し、ランダム・メルクル分岐クエリが安全に行えるようにデータの冗長性を確保する。次に、行のランダムな線形結合を計算し、新しい結合行が実際に気になる計算値を含むように係数を設計する。この新しく作成された行(128ビットの行として再解釈される)と、Merkle分岐を持つランダムに選択された列が検証者に渡される。
その後、バリデータは「拡張行の組み合わせ」(というより拡張列)と「拡張列の組み合わせ」を実行し、2つが一致することを検証する。次に列の組み合わせを計算し、それが証明者によって宣言された値を返すことをチェックする。これが我々の証明システム(より正確には、証明システムの重要な構成要素である多項式コミットメントスキーム)である。
まだカバーしていないものは?
行を拡張する効果的なアルゴリズムで、検証者の計算効率を実際に改善するために必要です。ここで説明されているように、バイナリフィールドの高速フーリエ変換を使用します(ただし、この投稿では再帰展開に基づかない、より効率の悪い構造を使用しているため、正確な実装は異なります)。
算術化。F(X+2)-F(X+1)-F(X)=Z(X)*H(X)のように、計算の隣接ステップを関連付けることができるので、単項式多項式は便利です。超立方体では、「次のステップ」は「X+1」よりもはるかに解釈しにくい。(kのべき乗であるX+kとすることもできるが、このジャンプ動作はBiniusの重要な利点の多くを犠牲にしている。ビニウス論文は解決策を記述している(4.3節参照)。 しかし、これ自体が「深いウサギの穴」なのである。
値固有のチェックを安全に行う方法。フィボナッチの例では、重要な境界条件であるF(0)=F(1)=1とF(100)の値をチェックする必要があります。しかし "オリジナルの "ビニウスでは、既知の計算点でチェックするのは安全ではありません。いわゆる和チェックプロトコルを使って、既知の計算チェックを未知の計算チェックに変換するかなり簡単な方法がありますが、ここではその話はしません。
ルックアップ・プロトコルは、超効率的な証明システムを作るために最近広く使われているもう一つの技法です。
平方根の検証時間を超えて。平方根は高価です。Biniusの証明2の32乗のビットは約11MBもあります。これを補うには、他の証明システムを使って「ビニウス証明の証明」を作ることで、ビニウス証明の効率とより小さな証明サイズを得ることができます。もう一つの選択肢は、より複雑なFRI-biniusプロトコルで、多対数サイズの証明を作成します(通常のFRIと同じです)。
Biniusが「SNARK Friendliness」に与える影響。基本的な要約は、Biniusを使用する場合、計算を「算術演算フレンドリー」にすることに気を配る必要がなくなるということです。「通常の」ハッシュは従来の算術ハッシュよりも効率的ではなくなり、モジュロ2の32乗やモジュロ2の256乗は、モジュロの乗算に比べて頭痛の種ではなくなります。しかし、これは複雑なトピックだ。すべてが2進数で行われると、多くのことが変わります。
バイナリフィールドベースの証明技術が今後数ヶ月でさらに向上することを期待しています。
「エーテルアライメント」には、価値観のアライメント、技術的アライメント、経済的アライメントなどが含まれる。
 JinseFinance
JinseFinanceこの記事は、あなたがすでにSNARKとSTARKの基本を理解していることを前提としています。もしそれらに馴染みがなければ、この記事の前のセクションを読んで基本を理解することをお勧めします。
 JinseFinance
JinseFinanceETH,ヴィタリックの最新記事Golden Financeの解説,イーサの魂と暗号世界の本質が残る。
 JinseFinance
JinseFinanceヴィタリックは4人の共著者と共同で、ブロックチェーン領域で最も差し迫った問題のひとつに対処するために設計された「プライバシープール」として知られる技術的驚異を紹介する研究論文を発表した。
 Catherine
Catherine新しいアップデートには、MEVの問題を解決するのに役立つ「The Scourge」が含まれています。
 Beincrypto
BeincryptoSoulbound トークンから超合理的な DAO まですべてをカバーする 10 年間のエッセイは、イーサリアムと暗号について語っています。
 Coindesk
Coindeskイーサリアムの発明者であるヴィタリック・ブテリンと彼の父であるドミトリー・“ディマ”・ブテリンは、暗号市場、ボラティリティ、投機家について話しました。 ...
 Bitcoinist
BitcoinistPoW と比較して、PoS は優れたブロックチェーン セキュリティ メカニズムです。
 链向资讯
链向资讯PoW と比較して、PoS はより優れたブロックチェーン セキュリティ メカニズムです。
 Ftftx
Ftftx南東ヨーロッパの小さな国は、イーサリアムの共同創設者に市民権を付与することで、ブロックチェーン規制の濁った水をふるいにかけ始めています。
 Cointelegraph
Cointelegraph