スマ
私たちは暗号通貨を中央集権的な取引所で保有しています。中央集権的な取引所での取引は非常に便利で速く、ビットコインがリリースされて以来10年間、多くの中央集権的な取引所が市場に誕生し、ユーザーにとって暗号通貨の売買が非常に容易になりました。しかし、中央集権的な取引所のブームとともに、詐欺や悪質なマネーロンダリングが常態化している。ニフティはこのため、取引所の突然の崩壊と創設者の謎の死を描いた特別プロモーション映画「誰も信じるな、仮想通貨サスペンス[1]」を制作した。特に2022年にFTXが債務超過で破産宣告を受け、世界中に衝撃を与え、多くのユーザーやファンド会社に莫大な損失を与えた。
実際、暗号通貨の分野だけでなく、他の伝統的な分野でも、不正会計によって投資家がだまされてきた。例えば、21世紀初頭に世界を揺るがしたエンロンのスキャンダル。エンロンは『フォーチュン』誌から6年連続で「アメリカで最も革新的な企業」に選ばれていたが、数千億ドルの資産を持つ企業でありながら、2002年に数週間であっという間に倒産した。もうひとつの例はエバーグランデで、同社は建築に充てられた資金を他の用途に流用し、最終的には30年の住宅ローンを抱えた無数の住宅所有者が家が崩壊するのを待つ結果となった。
さまざまな分野で不正が横行する背景には、監査や会計のプロセスそのものが完全にオープンで透明なものではなく、腐敗や不正の余地が非常に大きいということがある。しかし、企業の利益と投資家のプライバシーを守るために、重要な財務データを完全にオープンで透明なものにすることはできません。そのため、規制の強化に加え、金融詐欺への対応は良い解決策とは言えませんでしたが、ゼロ知識証明技術が徐々に成熟してきたことで、この考えに対する新たな解決策が見えてきました。
すべてのユーザーが、金融詐欺があるかどうかを資産の自分の部分を検証することができれば、ユーザーの検証が十分に大きい限り、組織は金融詐欺の難易度を行うに行きたい非常に高くなります。そしてまた、検証プロセスはゼロ知識であるため、検証データはネットワークを介して送信され、第三者がデータを傍受しても、彼はユーザーの本当の資産が何であるかを知らないので、検証プロセスは完全にネットワーク上でオープンに表示することができます。ゼロ知識証明技術の助けにより、多くの監査はもはやビッグ4会計事務所のような特定の組織だけが密室で秘密裏に行うものではなくなった。むしろ、あらゆる利害関係者が参加できるオープンなプロセスなのだ。
Summa[2]はPSEの研究プロジェクトで、zkアプローチを使ってユーザー資産の検証を行うことを目的としています。この記事の残りの部分では、プロジェクトの概要と技術的な実装について説明します。
契約
Summaの全体的なデータフローを図に示します。スマートコントラクトは主にパブリックデータの保存と検証のために使用されます。これは必ずしもEtherに縛られているわけではなく、Solanaのような他のブロックチェーンにデプロイすることができます(Halo2がブロックチェーンをサポートしている限り、このプロジェクトのコントラクトの一部はHalo2のプルーフ[3]によって生成されます)。

図中のCustodianは中央集権的な取引所を表しています。取引所を表している。コントラクトは取引所によってチェーン上に展開され、コントラクトの所有権は取引所が所有し、公開データは取引所によってのみ提出される。公開データは2つの部分で構成され、1つは取引所が管理するチェーンの基本情報とデジタル署名です。

この2番目の部分は、メルクル和ツリーのルートハッシュ、ルート残高など、チェーン上の資産に関する情報です(2番目の部分は、メルクル和ツリーのルートハッシュ、ルート残高(チェーン上の資産数、例えば何BTC)を含むチェーン上の資産に関する情報であり、zk証明のインスタンス入力として使用されます。
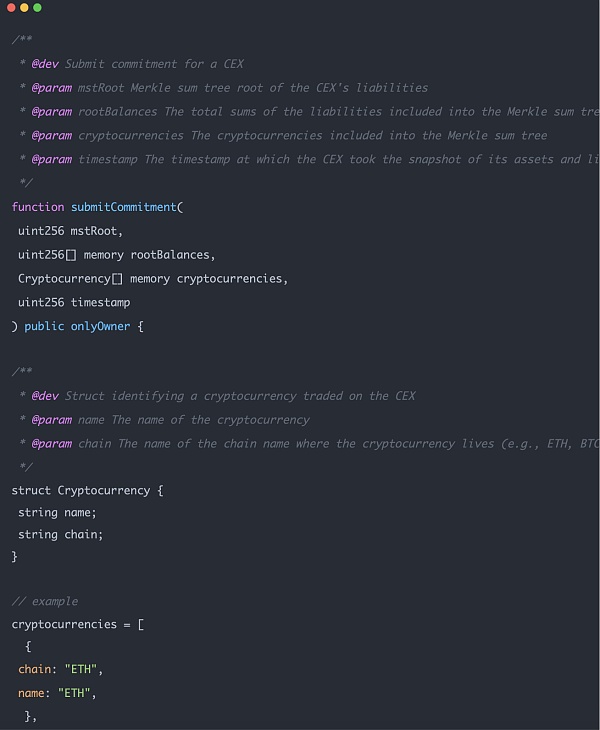
データのこれらの部分はどちらも、(ルートハッシュを除いて)オンチェーンで簡単かつ公に照会可能です。取引所がこのデータで不正を行うのは非常に難しい。誰でもコントラクトに保存されたデータとブロックチェーンのアドレス上の実際のデータ結果を比較することができます。
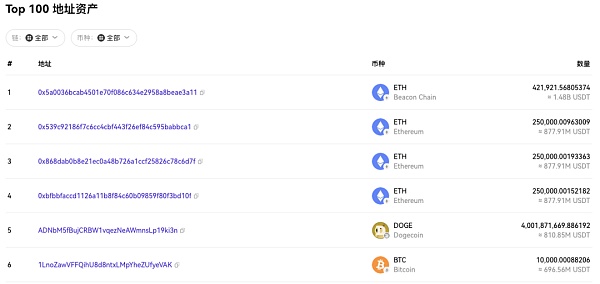
プルーフ生成は現在、取引所によって生成されています。ユーザーは検証が必要な鍵情報を取引所に提出し、取引所は証明を生成してユーザーに返します。
最後に、Proof Verifyはユーザーとコントラクト間の直接対話です。コントラクトのこの部分は、Halo2回路によってSolidityコードに変換され、別の検証コントラクトとしてチェーン上に展開されます。
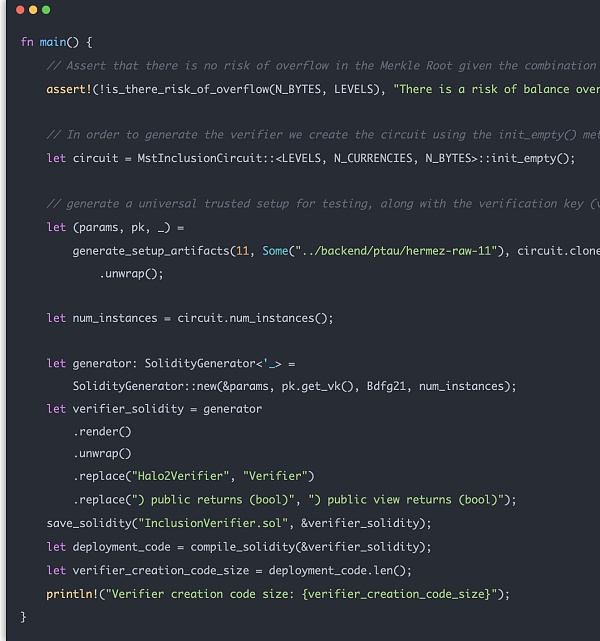
これは、証明を渡すことで、実際の使用においてチェーン内で計算および検証することができます。
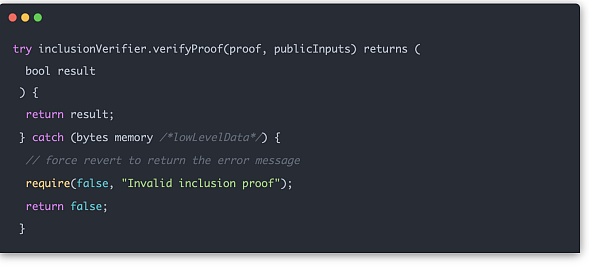
以下のコード例が実際に使用されているハッシュ関数で、ハッシュ計算自体はすべてビット演算を使用せず、加算と乗算のみを使用していることがわかります。足し算と掛け算だけなので、zkフレンドリーです。
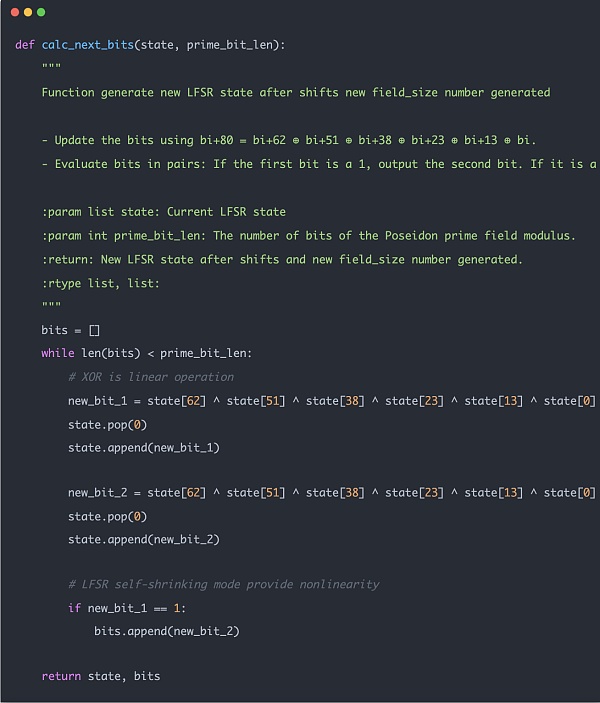
zkデータ計算が従来の手続き型計算と異なる点は、zkデータを有限領域上で計算しなければならない点であり、メルクルツリーを構築する際に各ノードのデータが有限領域を超えないようにする必要がある。
範囲チェックの一般的な原理は、以下の例に示すものと同様である。まず、入力データを8ビット長に切り詰めます。そして、次の値が計算されるたびに、下の例のように計算されます。範囲チェック回路は、実際には、diff = z_cur - z_next * Expression::Constant(Fp::from(1 << 8)) が中間結果によって制約される必要があります。code>を使用して制約を行い、差分が8ビット値以内であることを要求します。このようにして、32ビットのデータ制約の場合、4つの計算セルと256のルックアップテーブルを占有するだけでよく、そして、最上位ビットが0であるインスタンス制約を使用することができます。もしこのような設計でなければ、単純に32ビットの値域チェックを行い、ルックアップテーブルのサイズを必要とし、明らかにこのような回路は大きすぎて、実用的に適用することはできません。
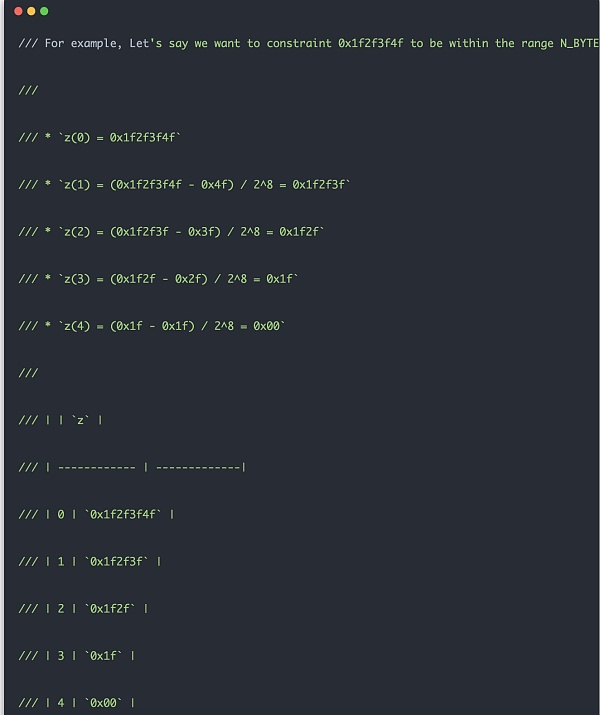
これらの補助構造が整ったところで、いよいよ正式にメルクルサムツリーを構築していきます。各ユーザー入力はエントリーと呼ばれ、次のような構造になっています:
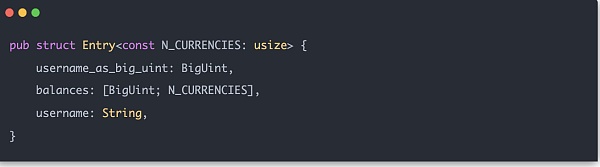
メルクルツリーの真ん中のノードのハッシュは、H(LeftChild.balance[0] + RightChild.balance[0] + MerkleTree.HKXEsXhOK6Lab.png) として計算されます。RightChild.balance[0], LeftChild.balance[1] + RightChild.balance[1], ...LeftChild.balance[N_CURRENCIES - 1] + RightChild.balance[N_CURRENCIES - 1], LeftChild.hash, RightChild.hash), したがって、実際に計算されるvec配列の長さはN_CURRENCIES + 2となります。
さて、メルクルツリー全体を構築しましょう。リーフノードは簡単で、EntryをNodeに変換するだけです。中間ノードはレイヤーごとに構築する必要があり、各中間ノードの値は次のレイヤーの左右のサブツリーの値に関連している。最後に、計算された中間ノードの結果がツリーの配列に入れられます:
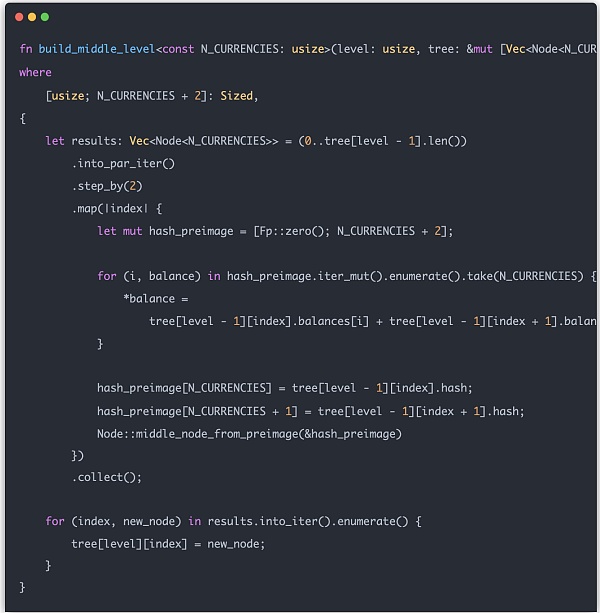
次に、メルクルツリーを使ってzk証明を構築します。zkは、ユーザーのエントリーが確かにそのメルクルツリー上にあることを証明します。メルクルツリー。そこでまず、特定のエントリーにインデックスを付け、メルクルツリーに基づいてzk証明に必要なデータ構造を生成する必要がある。
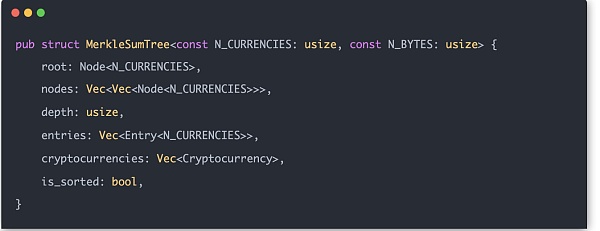
0と1を設定することで、式全体を0にするという制約効果をさりげなく実現できます。
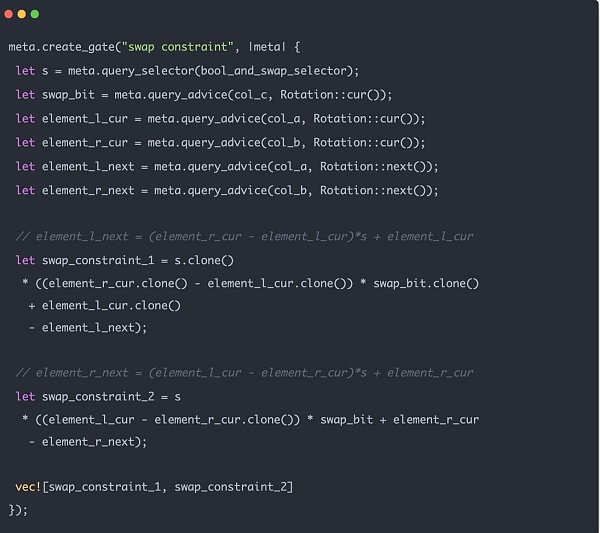
メルクル木zk制約には2つの主要な部分があります。1つはスワップ制約で、交換が上の図の真の順序で証明を実際に生成することを保証します。もう1つはバランス制約で、親ノードのバランスは左の子ノードと右の子ノードの合計に由来します。バランスに関する和の制約は比較的単純なので、ここではスワップの制約に注目しましょう。先に紹介したMerkle zkツリーのデータ構造sibling_middle_node_hash_preimagesは配列であり、位置情報を含んでいません。図の破線のボックスの位置が、本来あるべきツリーの左側にあるか右側にあるかは、path_indicesの0と1によって決まる。つまり、値が0のときは生成親が左にあり、同じレベルにある対応する兄弟が右にあることを確認し、値が1のときはその逆であることを確認しなければなりません。
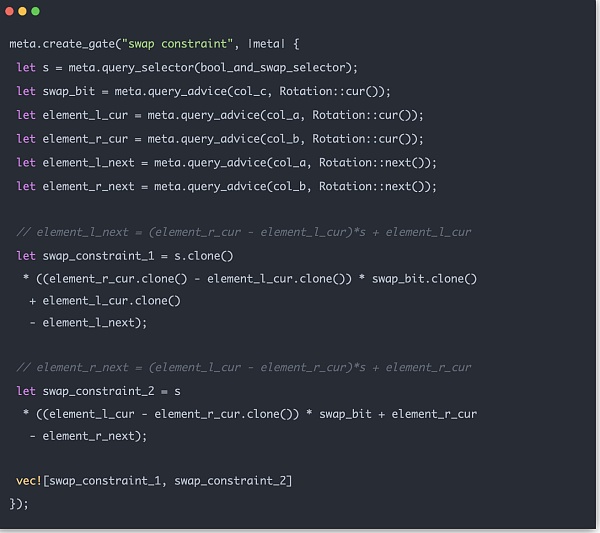
全体的なMerkle Sum Tree zk証明プロセスは、データをレイヤーごとに処理し、対応する位置データをzk制約回路に入力します。チェックする。最終的な出力はルートノードのハッシュと合計残高であり、これは契約書の対応するデータと整合している必要があり、整合性を検証するためにインスタンスを使用する。すべての検証に問題がなければ、メルクルツリー全体の証明が完了する。
ソルベンシー・ベリファイ
証明を生成するプロセスは、ユーザーが取引所に要求し、取引所が証明データを返し、ユーザーがスマートコントラクトで検証するというものです。現在のところ、プロジェクトは取引所をバイパスしたユーザーによるプルーフ生成をサポートしていないが、将来的には検討される方向かもしれない。取引所が証明を返すのではなく、ユーザーが直接証明を生成する。メルクルツリーのルート検証の時間複雑度はlog(n)なので、おそらくユーザーのデバイスで検証を行うのにそれほど時間はかからないだろう。これは分散化のセキュリティをさらに強化する。
参考文献
[1]
誰も信じるな!仮想通貨サスペンス:https://www.p>
[3]
生成されたHalo2の証明:https://github.com/privacy-scaling-explorations/halo2-。solid-verifier
[4]
ポセイドン・ハッシュ:https://github.com/ingonyama-zk/poseidon-hash
[5]
パラメータ準備段階とハッシュ操作段階: https://autoparallel.github.io/overview/index.html
[6]
リニアフィードバックシフトレジスタ:https://en.wikipedia.org/wiki/Linear-feedback_shift_register
[7]
ethers rs: https:/./github.com/gakonst/ethers-rs
推薦図書
ZKインサイト・シリーズ
ZKP学習ノート
ウェンビル ポッドキャスト
リサーチ分析シリーズ
ユニスワップ細かいめくりシリーズ
Antalpha Labs は非営利の Web3 開発者コミュニティです。
公式サイト: https://labs.antalpha.com
Twitter: https://labs.antalpha.com
Twitter:
Twitter: https://twitter.com/Antalpha_Labs
Youtube: https://www.youtube.com/channel/UCNFowsoGM9OI2NcEP2EFgrw
Contact Us: [email protected]
 JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance Bitcoinworld
Bitcoinworld Numen Cyber Labs
Numen Cyber Labs Bitcoinist
Bitcoinist Cointelegraph
Cointelegraph Cointelegraph
Cointelegraph Cointelegraph
Cointelegraph