Author: Vitalik, founder of Ethereum; Translation: 0xjs@黄金财经
In Ethereum, until recently, resources were limited and priced using a single resource called "Gas". Gas is a measure of the "computational amount" required to process a given transaction or block. Gas combines multiple types of “effort” together, most notably:
Raw computation (e.g. ADD, MULTIPLY)
Reading and writing Ethereum storage (e.g. SSTORE, SLOADETH transfers)
Data bandwidth
The cost of generating the ZK-SNARK proof for the block
For example, this transaction I sent (https://etherscan.io/tx/0xc5195b64cc333b8098d71fbd0f032e05d4545917e3b0be8d123ab06e1ad7998e) cost a total of 47,085 Gas. This is broken down into (i) a "base cost" of 21,000 gas, (ii) 1,556 gas for the call data bytes that make up part of the transaction, (iii) 16,500 gas for reading and writing storage, (iv) 2,149 gas for log generation, and the rest for EVM execution. The transaction fee a user must pay is proportional to the gas consumed by the transaction. A block can contain a maximum of 30 million gas, and the gas price is constantly adjusted via the EIP-1559 target mechanism to ensure that blocks contain an average of 15 million gas.
This approach has one major efficiency: because everything is merged into a single virtual resource, it leads to a very simple market design. It's easy to optimize transactions to minimize costs, it's relatively easy to optimize blocks to charge the highest possible fees (excluding MEV), and there are no weird incentives to encourage certain transactions to be bundled with other transactions to save fees.
But this approach also has a major inefficiency: it treats different resources as interconvertible, while the actual underlying limit of what the network can handle is not. One way to understand this problem is to look at this diagram:
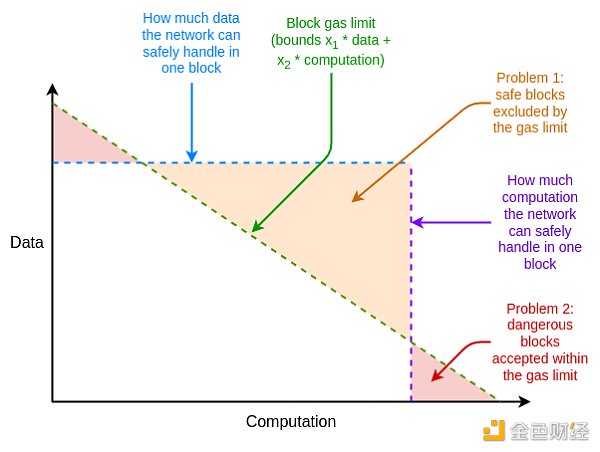 The gas limit enforces the following constraint: x1*data+x2*computation<N. The actual underlying security constraint is typically closer to max(x1*data, x2*computation)<N. This discrepancy causes the gas limit to unnecessarily exclude blocks that are actually secure, or accept blocks that are actually unsafe, or some mixture of the two.
The gas limit enforces the following constraint: x1*data+x2*computation<N. The actual underlying security constraint is typically closer to max(x1*data, x2*computation)<N. This discrepancy causes the gas limit to unnecessarily exclude blocks that are actually secure, or accept blocks that are actually unsafe, or some mixture of the two.
If there are ? resources with different security constraints, then one-dimensional gas can reduce throughput by up to a factor ?. As a result, there has long been interest in the idea of multidimensional gas, and with EIP-4844, we actually have multidimensional gas running on Ethereum today. This post explores the benefits of this approach and the prospects for further enhancements.
Blobs: Multidimensional Gas in Dencun
At the beginning of this year, the average Ethereum block size was 150 kB. A large part of that size is Rollup data: data that Layer 2 protocols store on-chain for security purposes. This data is expensive: while Rollup transactions cost about 5-10 times less than corresponding transactions on Ethereum L1, this cost is still too high for many use cases.
Why not reduce the gas cost of calldata (currently 16 gas per non-zero byte, 4 gas per zero byte) to make Rollups cheaper? We have done this before, and we can do it again. The answer here is: the worst-case block size is 30000000/16 = 1875000 non-zero bytes, and the network can barely handle blocks of that size already. If the cost were reduced by another factor of 4, the maximum capacity would increase to 7.5 MB, which would pose a huge security risk.
This problem was eventually solved by introducing a separate, easily rollup-friendly data space in each block, called a "blob". The two resources have different prices and different limits: after the Dencun hard fork, an Ethereum block can contain at most (i) 30 million gas, and (ii) 6 blobs, each of which can contain about 125 kB of call data. Both resources have separate prices, adjusted by a separate EIP-1559-like pricing mechanism, with the goal of an average of 15 million gas and 3 blobs per block.
As a result, rollups became 100x less expensive, and the volume of transactions on rollups increased more than 3x, while the theoretical maximum block size increased only slightly: from ~1.9MB to ~2.6MB.
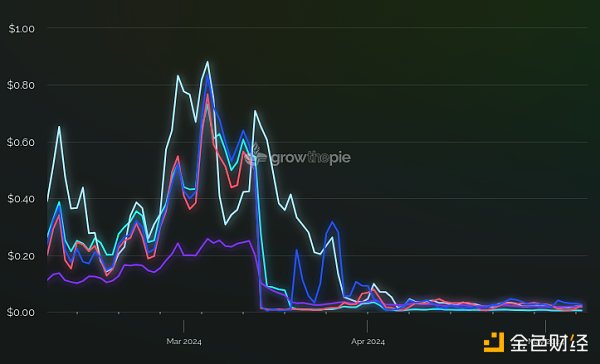 Rollup transaction fees, courtesy of Growthepie.xyz. The Dencun fork occurred on March 13, 2024, introducing multi-dimensionally priced blobs.
Rollup transaction fees, courtesy of Growthepie.xyz. The Dencun fork occurred on March 13, 2024, introducing multi-dimensionally priced blobs.
Multidimensional gas and stateless clients
In the near future, similar issues will arise with storage proofs for stateless clients. Stateless clients are a new type of client that will be able to validate the blockchain without storing much or any data locally. Stateless clients do this by accepting proofs of specific parts of Ethereum that the transactions in that block touched.
 Stateless clients receive a block, along with proofs of the current values of specific parts of the state (e.g. account balances, code, storage) that the block's execution touched. This allows nodes to validate blocks without any storage themselves.
Stateless clients receive a block, along with proofs of the current values of specific parts of the state (e.g. account balances, code, storage) that the block's execution touched. This allows nodes to validate blocks without any storage themselves.
A storage read costs 2100-2600 Gas, depending on the type of read, while storage writes are more expensive. On average, a block performs about 1000 storage reads and writes (including operations such as ETH balance checks, SSTORE calls SLOAD, contract code reads, etc.). However, the theoretical maximum is 30000000/2100=14285 reads. The bandwidth load of stateless clients is proportional to this number.
Today, the plan is to support stateless clients by moving Ethereum's state tree design from Merkle Patricia trees to Verkle trees. However, Verkle trees are not quantum resistant and are not optimal for the newer STARK proof system. Therefore, many are interested in supporting stateless clients via binary Merkle trees and STARKs - either skipping Verkle entirely or upgrading after a few years of the Verkle transition once STARKs become more mature.
Binary hash tree branching STARK proofs have many advantages, but they have a key weakness, which is that proofs take a long time to generate: while Verkle trees can prove over a hundred thousand values per second, hash-based STARKs can typically only prove a few thousand hashes per second, and proving each value requires a "branch" containing many hashes.
Given today's predicted numbers from super-optimized proof systems such as Binius and Plonky3, and specialized hashes such as Vision-Mark-32, we are likely to be in a state for some time where we can actually prove 1,000 values in less than a second, but not 14,285 values. This is fine on average per block, but a worst-case block (perhaps released by an attacker) would break the network.
Our "default" way of dealing with this situation is to reprice: make storage more expensive to read, to reduce the maximum per block to a safer point. However, we have done this many times before, and too many applications would become too expensive to do it again. A better approach would be multi-dimensional gas: limit and charge storage access separately, keeping average usage at 1,000 storage accesses per block, but setting the per-block limit to, say, 2,000.
Multi-dimensional Gas More Generally
Another resource worth considering is state size growth: operations that increase the size of the Ethereum state, for which full nodes will need to hold the full state. State size growth is unique in that the rationale for limiting state growth comes entirely from long-term sustained usage, not peaks. Thus, adding a separate gas dimension for state size increasing operations (e.g., zero to non-zero SSTORE, contract creation) might be valuable, but the goal is different: we could set a floating price to target a particular average usage, but not set a per-block limit at all.
This shows one of the powerful properties of multi-dimensional Gas: it lets us ask separately: (i) what is the ideal average usage of each resource, and (ii) what is the safe maximum usage per block. Instead of setting the gas price based on a maximum per block, we average usage, which gives us 2 degrees of freedom to set 2 parameters and adjust each one based on our concerns about the security of the network.
More complex cases, such as two resources having partially additive security concerns, can be handled by making opcodes or resources cost a certain amount of multiple types of gas (e.g., a zero-to-nonzero SSTORE might cost 5000 gas for stateless client proofs and 20000 gas for storage inflation).
Maximum per transaction: A weaker but simpler way to get multi-dimensional gas
Let x1 be the gas cost of data and x2 be the gas cost of computation, so in the one-dimensional gas system we can write the gas cost of a transaction as gas=x1*data+x2*computation
In the new scheme, we define the gas cost of a transaction as: gas=max(x1*data, x2*computation)
That is, instead of charging for data plus computation, a transaction is charged for which of the two resources it consumes more. This can be easily extended to cover more dimensions (e.g. max(…,x3*storage_access)).
It should be easy to see how this improves throughput while maintaining security. The theoretical maximum amount of data in a block is still GASLIMIT/x1, exactly the same as in the one-dimensional gas scheme. Similarly, the theoretical maximum amount of computation is GASLIMI/x2, again exactly the same as in the one-dimensional gas scheme. However, the gas cost of any transaction that consumes both data and computation is reduced.
This is approximately the scheme adopted in the proposed EIP-7623 to reduce the maximum block size while further increasing the blob count. The precise mechanism in EIP-7623 is slightly more complicated: it keeps the current calldata price of 16 gas per byte, but adds a "floor price" of 48 gas per byte; transactions pay the higher of (16 * bytes + execution_gas) and (48 * bytes). Thus, EIP-7623 reduces the theoretical maximum transaction calldata in a block from about 1.9 MB to about 0.6 MB, while keeping the cost unchanged for most applications. The benefit of this approach is that it is very small compared to the current one-dimensional gas scheme, so it is very easy to implement.
It has two disadvantages:
1. Transactions that use a lot of one resource will still be charged unnecessarily large fees, even if all other transactions in the block use only a small amount of that resource.
2. It incentivizes data-intensive and compute-intensive transactions to be combined into a single bundle to save costs.
I think that EIP-7623-style rules, both for transaction call data and other resources, could bring large enough benefits to be worthwhile even with these drawbacks. However, there is a more ideal approach if we are willing to invest the (significantly higher) development effort.
Multidimensional EIP-1559: A more difficult but ideal strategy
Let's first review how "regular" EIP-1559 works. We will focus on the version introduced in EIP-4844 for blobs because it is more mathematically elegant.
We track a parameter, excess_blobs. During each block, we set:
excess_blobs <-- max(excess_blobs + len(block.blobs) - TARGET, 0)
Here TARGET = 3. That is, if a block has more blobs than the target, excess_blobs increases, and if a block has fewer blobs than the target, it decreases. We then set blob_basefee = exp(excess_blobs / 25.47), where exp is an approximation of the exponential function, exp(x).
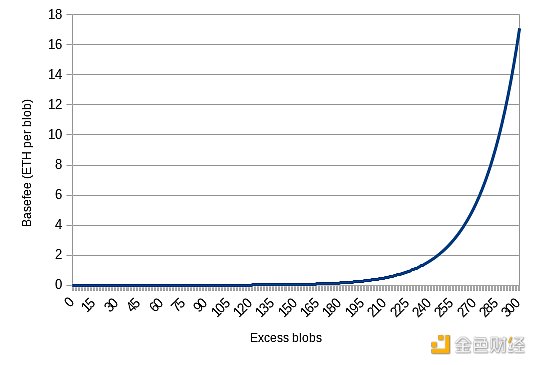 That is, every time excess_blobs increases by about 25 times, the blob base fee increases by about 2.7 times. If blobs become too expensive, average usage will drop, and then excess_blobs will start to drop, automatically lowering the price again. The price of blobs is constantly adjusted to ensure that, on average, blocks are half full - that is, each block contains an average of 3 blobs.
That is, every time excess_blobs increases by about 25 times, the blob base fee increases by about 2.7 times. If blobs become too expensive, average usage will drop, and then excess_blobs will start to drop, automatically lowering the price again. The price of blobs is constantly adjusted to ensure that, on average, blocks are half full - that is, each block contains an average of 3 blobs.
If there are short-term spikes in usage, a limit occurs: each block can only contain a maximum of 6 blobs, in which case transactions can compete with each other by increasing their priority fees. However, under normal circumstances, each blob only has to pay the blob_basefee plus a little extra priority fee as an incentive to be included.
This kind of gas pricing has existed in Ethereum for years: back in 2020, EIP-1559 introduced a very similar mechanism. With EIP-4844, we now have two separate floating prices for Gas and Blobs.

Gas base fees in gwei for one hour on May 8, 2024. Source: ultrasonic.money
In principle, we could add more separately floating fees for storage reads and other types of operations, but there is a caveat that I will explain in detail in the next section.
For users, the experience is very similar to today: instead of paying one base fee, you pay two base fees, but your wallet can abstract this from you and only show you the expected fee and the maximum fee you can expect to pay.
For block builders, most of the time the optimal strategy is the same as it is today: include anything that is valid. Most blocks are not full - either in gas or in blobs. A challenging case is when there is enough gas or enough blobs to exceed the block limit, and builders need to potentially solve a multi-dimensional knapsack problem to maximize their profits. However, even if reasonably good approximations exist, the gains gained by crafting a proprietary algorithm to optimize for profits in this case are much smaller than the gains gained by doing the same thing with MEV.
For developers, the main challenge is the need to redesign the functionality of the EVM and its surrounding infrastructure, which is currently designed around one price and one limit, to one that accommodates multiple prices and multiple limits. One problem for application developers is that optimization becomes slightly harder: in some cases you can no longer unambiguously say that A is more efficient than B, because if A uses more calldata and B uses more execution, then it is more expensive when calldata is cheap and more expensive when calldata is expensive. However, developers are still able to get reasonably good results by optimizing based on long-term historical average prices.
Multidimensional Pricing, the EVM, and Sub-calls
There is one problem that doesn't appear in blobs, or in EIP-7623, or even in a "full" multidimensional pricing implementation of calldata, but it does if we try to price state access or any other resource individually: gas limits in sub-calls.
Gas limits in the EVM exist in two places. First, every transaction sets a gas limit that limits the total amount of gas that can be used in that transaction. Second, when a contract calls another contract, that call can set its own gas limit. This allows contracts to call other contracts that they don't trust and still guarantee that they have gas left after the call to perform other computations.
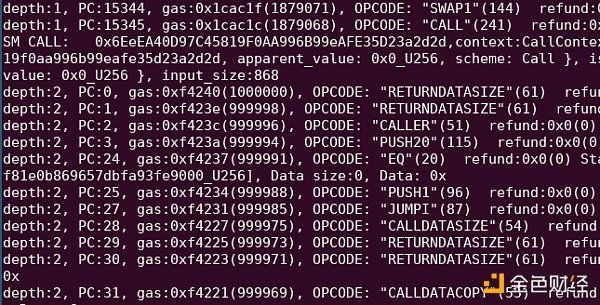
A trail of account abstraction transactions, where one account calls another and only provides a limited amount of gas to the callee, ensuring that the external call can continue to run even if the callee consumes all the gas allocated to it.
The challenge is: making Gas multi-dimensional between different types of execution would seem to require sub-calls to provide multiple limits for each type of Gas, which would require really deep changes to the EVM and is incompatible with existing applications.
This is one of the reasons why multi-dimensional gas proposals usually stop at two dimensions: data and execution. Data (whether transaction calldata or blobs) is only allocated outside the EVM, so nothing needs to change inside the EVM to make calldata or blobs priced separately.
We can come up with an "EIP-7623-style solution" to this problem. Here's a simple implementation: During execution, charge 4 times the fee for storage operations; to simplify analysis, we assume each storage operation is 10000 gas. The transaction ends and refunds min(7500 * storage_operations, execution_gas). The result is that after deducting the refund, the user needs to pay the following fee:
execution_gas + 10000 * storage_operations - min(7500 * storage_operations, execution_gas)
This is equal to:
max(execution_gas + 2500 * storage_operations, 10000 * storage_operations)
This reflects the structure of EIP-7623. Another approach would be to keep track of storage_operations and execution_gas in real time, and charge 2500 or 10000 gas depending on how much max(execution_gas + 2500 * storage_operations, 10000 * storage_operations) is accumulated when the opcode is called. This avoids transactions needing to over-allocate gas, which is mostly recovered through refunds.
We don't get fine-grained permissions for subcalls: a subcall could potentially consume all of a transaction's "allowance" to do cheap storage operations. But we do get something nice enough where a contract making a subcall can set limits and ensure that once the subcall has finished executing, the main call still has enough gas to do any post-processing it needs to do.
The simplest "full multidimensional pricing solution" I can think of is this: we treat the subcall gas limits as proportional. That is, suppose there are
? different types of executions, and each transaction sets a multidimensional limit of ?1…??. Suppose at the current execution point, the remaining gas
is ?1…??. Suppose CALL invokes an opcode, with a subcall gas limit S. Let s1=S, and hence s2=s1/g1*g2, s3=s1/g1*g3, and so on.
That is, we treat the first type of gas (actually the VM execution) as a privileged "account unit", and then allocate the other types of gas so that subcalls get the same percentage of the available gas in each type. This is a bit ugly, but it maximizes backwards compatibility. If we wanted to make the scheme more "neutral" between different types of gas, at the expense of backwards compatibility, we could simply have the subcall gas limit parameter represent a fraction of the remaining gas (e.g. [1...63] / 64).
In either case, however, it's worth emphasizing that once you start introducing multi-dimensional execution gas, the inherent ugliness increases, and it seems difficult to avoid.
So we are tasked with making a complex tradeoff: do we accept something uglier at the EVM level in order to safely unlock significant L1 scalability gains, and if so, which specific proposal is best for protocol economics and application developers?
Most likely, it's none of the ones I mentioned above, and there's still room to come up with something more elegant and better.
Special thanks to Ansgar Dietrichs, Barnabe Monoton, and Davide Crapis for their feedback and review.
 JinseFinance
JinseFinance
 JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance Davin
Davin Pr0phetMoggy
Pr0phetMoggy Bitcoinist
Bitcoinist Bitcoinist
Bitcoinist Others
Others Cointelegraph
Cointelegraph Cointelegraph
Cointelegraph