Bài viết mới nhất của Vitalik: Khám phá vòng tròn STARK

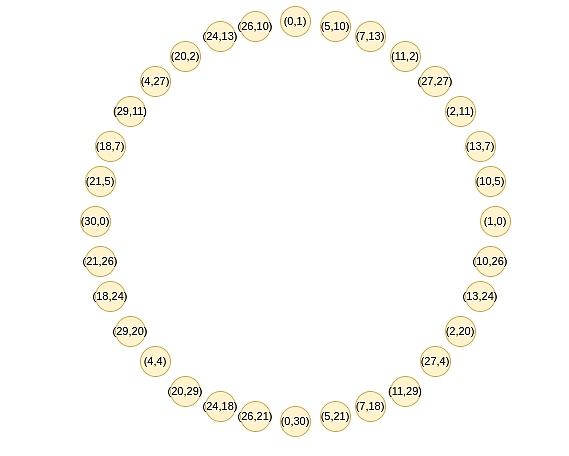
Các dấu chấm này tuân theo định luật cộng và nếu gần đây bạn đã học lượng giác hoặc phép nhân phức, bạn có thể thấy định luật này quen thuộc:

- https://unacademy.com/content/cbse-class- 11/study -material/mathematics/algebra-of-complex-numbers-multiplication/

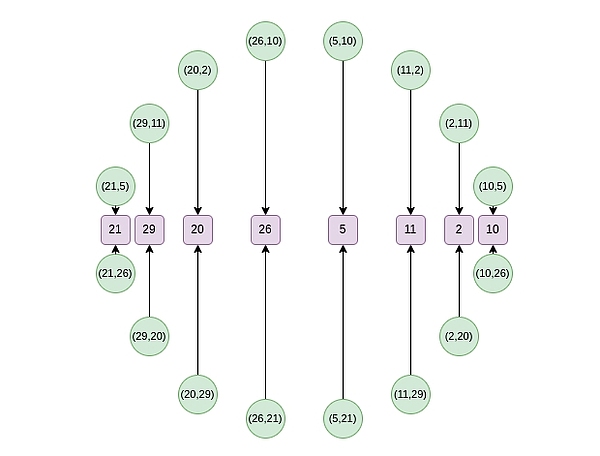
Từ vòng thứ hai trở đi, ánh xạ thay đổi:

Vòng tròn FFT

• https://vitalik.eth.limo/general/2019/05/12/fft.html< phần>

• https://www.researchgate.net/publication/353344649_Elliptic_Curve_Fast_Fourier_Transform_ECFFT_Part_I_Fast_Polynomial_Algorithms_over_all_Finite_Fields

Từ đây, hãy tìm hiểu thêm một số chi tiết bí truyền dành cho những người triển khai STARK vòng tròn, so với những điều này thông thường chi tiết sẽ khác so với STARK.

Khởi nghiệp

• https:/ /eprint.iacr.org/2019/336

Đa thức biến mất

Thứ tự bit đảo ngược

Hiệu quả

Do đó, hãy khoanh tròn STARK thực sự là rất gần với mức tối ưu! Binius thậm chí còn mạnh mẽ hơn vì nó cho phép trộn và kết hợp các miền có kích thước khác nhau, mang lại khả năng đóng gói bit hiệu quả hơn cho mọi thứ. Binius cũng cung cấp tùy chọn để thực hiện các phép cộng 32 bit mà không cần sử dụng bảng tra cứu. Tuy nhiên, những lợi ích này phải trả giá bằng (theo ý kiến ​​​​của tôi) độ phức tạp về mặt lý thuyết cao hơn đáng kể, trong khi vòng tròn STARK (và STARK thông thường dựa trên BabyBear) về mặt khái niệm khá đơn giản.

Kết luận: Tôi nghĩ gì về STARK hình tròn?

So với STARK thông thường, Circle STARK không mang lại nhiều sự phức tạp bổ sung cho các nhà phát triển. Trong quá trình triển khai, ba vấn đề trên về cơ bản là điểm khác biệt duy nhất tôi thấy so với FRI thông thường. Phép toán đằng sau "đa thức" mà Circle FRI thực hiện khá phản trực giác và phải mất một thời gian để hiểu và đánh giá cao. Nhưng điều xảy ra là sự phức tạp này bị ẩn đi nên các nhà phát triển không nhìn thấy quá nhiều về nó. Sự phức tạp của toán học Vòng tròn được gói gọn chứ không mang tính hệ thống.

• https://vitalik.eth.limo/general/2022/02/28/ complex.html

Hiểu FRI vòng tròn và FFT vòng tròn cũng là một cách tiếp cận trí tuệ tốt để hiểu các "FFT kỳ lạ" khác: tốt nhất Đáng chú ý là FFT miền nhị phân, trước đây được sử dụng trong Binius và LibSTARK, cũng như các cấu trúc kỳ lạ hơn, chẳng hạn như FFT đường cong elip, sử dụng nhiều ánh xạ một số và hoạt động tốt với các phép toán điểm trên đường cong elip.

• https://github.com/ethereum/research/blob/master/binius/ nhị phân_ntt.py#L60

• https://github.com/elibensasson/libSTARK

• https://arxiv.org/abs/2107.08473

Bằng cách kết hợp Mersenne31, BabyBear và công nghệ miền nhị phân như với tư cách là Binius, chúng tôi cảm thấy rằng chúng tôi đang đạt đến giới hạn về hiệu quả "lớp cơ sở" của STARK. Tại thời điểm này, tôi hy vọng giới hạn của tối ưu hóa STARK sẽ chuyển sang hướng số học hiệu quả nhất của các nguyên hàm như hàm băm và chữ ký (và tối ưu hóa chính các nguyên hàm đó cho mục đích này), các cấu trúc đệ quy để mở khóa nhiều khả năng song song hơn, Số học hóa các máy ảo để cải thiện kinh nghiệm của nhà phát triển và các nhiệm vụ cấp cao khác.