苦い宗教:拡張の法則をめぐるAIの聖戦
AIのコミュニティは、その将来と神を創造するのに十分な大きさかどうかをめぐる教義上の争いに巻き込まれている。
 JinseFinance
JinseFinance
コンパイル:劉教鎖
教鎖注:これはハロルド・クリストファー・バーガーとピーター・ヴィジュンの共同論文「Bitcoin's time--based power-law andointegration revisited」の翻訳です。based power-law and coointegration revisited, 2024.1.31)を翻訳したもので、より理論的で、統計学の一定の基礎がある読者に適している。基礎が不十分な読者にも理解しやすくするため、まずティーチングチェーンを簡単に説明する。
いわゆる時間のべき乗モデルは、ここ数年いくつかの論文で紹介されている。
業界ではより有名な匿名アナリストの一人であるPlanBは、S2Fモデルとして知られるS2F硬度を使った価格モデルを大々的に提唱してきました。しかし残念ながら、S2Fモデルは間違っている。しかし、これはS2Fの指標が無意味であるという意味ではなく、S2Fの硬度の変化が、価格に関連して、PlanBが描くほど「過激」ではないということを意味している。
次のグラフは、べき乗モデルとS2Fモデルの関係を明確に示しています。
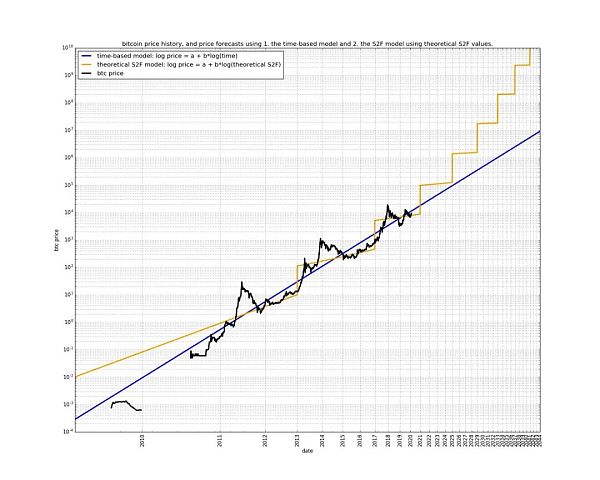
S2F モデルが、指数関数的な価格上昇を促すものとして、直線的な時間の経過を見ているのに対し、べき乗モデルは、指数関数的な価格上昇を促すものとして、直線的な時間の経過を見ています。べき乗則モデルは、指数関数的な価格上昇を促す指数関数的な時間の経過を考慮する。
教師は、生産を半減させることによって引き起こされる「相変化」を視覚化するためにS2F硬度を使用する傾向がありますが、ビットコインを両対数空間の線形回帰に変換するためにべき乗則モデルを使用します。べき乗モデルの優雅さは、サポートベクターマシン(SVM)特有の感触があるので、私の好みにぴったりです。
H. Burger & P. Vijnによる論文はこちらです。
* * *
ビットコインの時間ベースのべき乗則は、もともと2014年にGiovanniSantostasiによって2014年に提案され、2019年に(回廊または3パラメータモデルとして)再定式化された、ビットコイン価格と時間の関係を記述します。具体的には、このモデルは、ビットコイン発生ブロックからの日数の対数とビットコインUSD価格の対数の間の線形関係を記述します。
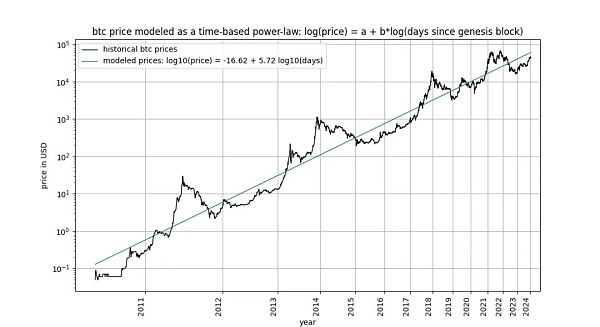
このモデルには、Marcel Burger氏、Tim Stolte氏、Nick Emblow氏など多くの批判者が集まっており、それぞれ「反論」を書いています。".この記事では、これら3つの批評の重要な論点の1つである、時間と価格の間に共同継起(cointegration)は存在しないという主張を解剖し、このモデルは「無効」であり、偽の関係を示しているに過ぎないと主張します。
これは本当に正しいのでしょうか?
本稿では、この疑問について詳しく見ていく。その結果、厳密に言えば、私たちのモデルも含め、時間依存モデルにおいて、共和分(cointegration)は存在し得ないと判断することになる。しかし、コヒーネレーションに必要な統計的性質の1つが、時間ベースのべき乗モデルに存在することは否定できない。したがって、我々は、時間ベースのべき乗モデルは狭い意味では共和分であり、我々の批判は見当違いであり、このモデルは完全に妥当であると結論づける。この結論は、「ストック・インクリメント・レシオ」(S2F)モデルにも、長期的な株価指数で観察される指数関数的成長にも同様に当てはまることを示す。
道に迷っていませんか?もしかしたら、「共和分」という用語に馴染みがないかもしれません。因果推論と非スプリアス関係の専門家であり、『The Book of Why』の著者でもあるジュデア・パールは、このテーマについて何も知らないと主張しています。私たちは、手元にある用語を完全に明らかにするよう努力します。
ツイッター上のビットコイン関連の議論における共分散をめぐる議論は興味深く、非常に興味深いものだった。株価上昇率」や「べき乗則」の信奉者の多くが混乱しています。興味のある読者は、「共分散とは何か」で検索すれば、自分の目で確かめることができる。時間の経過とともに、理解を深め、洗練された投稿者もいれば、混乱したまま、鞍替えしたり、道を踏み外したりする投稿者もいるようだ。私たちがこのトピックに焦点を当て始めたのは、今になってからです。
確率過程には確率変数が含まれます。確率変数の値はあらかじめ決まっているわけではありません。対照的に、決定論的過程は事前に正確に予測することができます。例えば、株式市場価格は、事前に資産価格を予測することができないため、確率変数である。したがって、株価やビットコイン価格のような時系列は、確率変数の観測値として扱います。
対照的に、時間の経過は決定論的なパターンに従う。1秒1秒は不確実性なく経過します。したがって、ある出来事が起きてからの継続時間は決定論的変数です。
コアンテグレーションを見る前に、コアンテグレーションの基礎となる概念である「定常性」を見てみましょう。
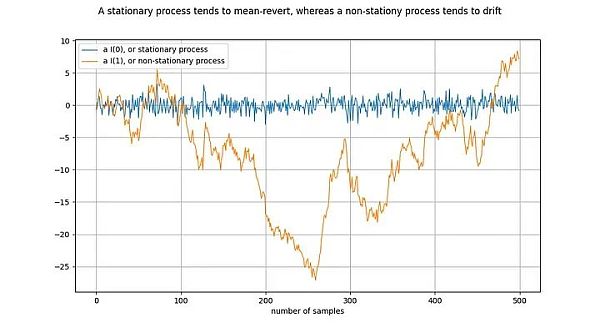
図の解釈:オレンジ色の線を一度微分すると、青色の線が得られます。I(1)時系列を一度差分するとI(0)時系列になる。
平滑過程(定常過程)とは、広い意味で、時間にわたって同じ性質を持つ確率過程です。例えば、定常過程では、平均と分散は決定されていて安定しています。定常時系列の同義語はI(0)である。定常過程に由来する時系列は「ドリフト」せず、平均(通常はゼロ)に収束するはずです。
非平滑過程の例としては、物理学におけるブラウン運動や粒子拡散のようなランダムウォークがあります。非平滑過程の特性(平均や分散など)は時間とともに変化するか、定義されない。非平滑過程はI(1)以上であるが、通常はI(1)である。非定常過程に由来する時系列は、時間とともに「ドリフト」する、すなわち、任意の固定値から逸脱する傾向がある。
I(1)という記号は、時系列が定常性に達するために何回「差分」する必要があるかを示しています。差分とは、時系列の値とその前の値との差を見つけるプロセスのことです。これは導関数を取ることとほぼ同じです。I(1)の時系列は、定常になるために1回差分する必要があります。
上のグラフは、青い時系列がオレンジの時系列を1回差分することによって得られるようにプロットされています。同様に、オレンジの時系列は青の時系列を積分することで得られます。
単位根過程は、rhoパラメータが1に等しいと推定される自己回帰モデル(より正確にはAR(1)型)を指します。rhoとrootは同じ意味で使うことができるが、rhoはプロセスの真値を意味し、これは通常未知であり、推定する必要がある。その結果が「ルート」値です。
rhoの値は、プロセスがどれだけ前の値を覚えているかを示します。
uは誤差項を指し、これは白色ノイズであると仮定されます。
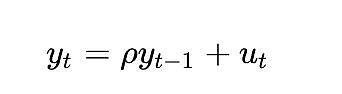
単位根過程は確率的放浪過程であり、非平滑です。ルート」またはrho値が1以下の過程はドリフトしない傾向があり、したがって滑らかです。1に近い(しかし1を下回る)値でも、長期的には(ドリフトではなく)平均回帰する傾向があります。このように、単位根過程は、根の値が1に非常に近い過程とは根本的に異なるという点で特別です。
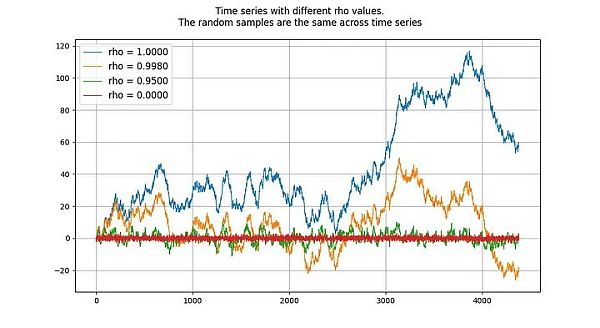
2 つの確率変数(この場合は時系列)間の共分散(共イグレーションの関係)の有無。.一対の変数が共分散するためには、両者が同じ積分次数を持ち、両者が非定常でなければならない。さらに(ここが重要なのだが)、2つの時系列の線形結合は滑らかでなければならない。
2つの時系列が非定常である場合、線形結合(この場合、単に2つの時系列の差を選択します)も通常は非定常です:
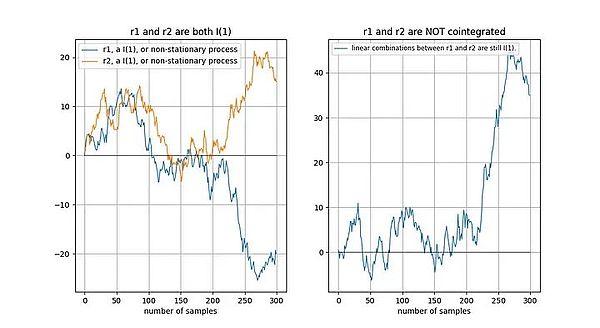
2つの非定常時系列が長期的に「同じように」ドリフトする場合、線形結合(この場合、r2- 0.5*r1を選びます)も非定常である可能性があります:
これは共分散シグナルの良い例です。
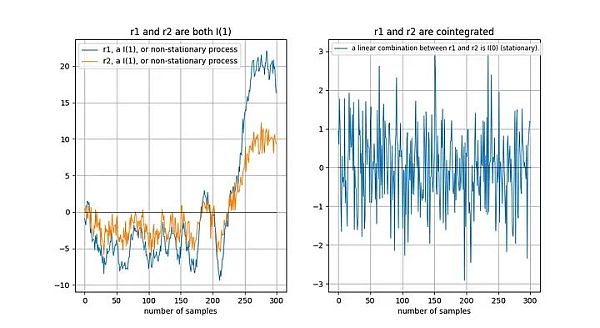
Tu et al [1]はコインテグレーション関係を直感的に説明しています:
「時系列間のコインテグレーション関係の存在は、それらが長期的に共通の確率的ドリフトを共有していることを意味する。長期的には共通の確率的ドリフトを持つ。"
なぜ滑らかでない2つの時系列の線形結合は滑らかなのでしょうか?モデルの誤差は、xとyの線形結合で与えられます:モデル誤差=y - a - b*x。我々は、モデル誤差が滑らかであること、すなわち時間とともにドリフトしないことを望む。モデル誤差が時間とともにドリフトするならば、それは我々のモデルが悪く、正確な予測ができないことを意味する。
EngleとGrangerによる論文「Cointegration and Error Correction: Representation, Estimation, and Tests」[2](Grangerはコインテグレーションの概念の発明者であり、2003年にノーベル経済学賞を受賞)では、以下のように定義されています。コアインテグレーションの主要概念と検定。この論文の鍵は、時系列が確率的であり、決定論的要素を持たないという仮定である(これについては後で触れる)。

決定論的なトレンドがある場合、分析前にそれを取り除く必要があります:

時間ベースのべき乗則では、2つの変数があります:
1.log_time:ブロックの作成からの日数の対数
2.log_price:価格の対数EngleとGrangerの定義では、両変数は決定論的要素を持たない確率変数でなければならず、非平滑でなければなりません。さらに、これら2つの変数の静的線形結合を見つけることができなければならない。そうでなければ、これら2つの変数の間に共同継起は存在しない。
詳細を掘り下げる前に、平滑化やコインテグレーションの概念を含まないモデルデータ自体のグラフをいくつか示しましょう。時間ベースのべき乗則は、直感的に非常に良く見えるフィットを生み出すことに注意してください。残差ベクトル(residuals vector)はすぐにはドリフトを示さない。
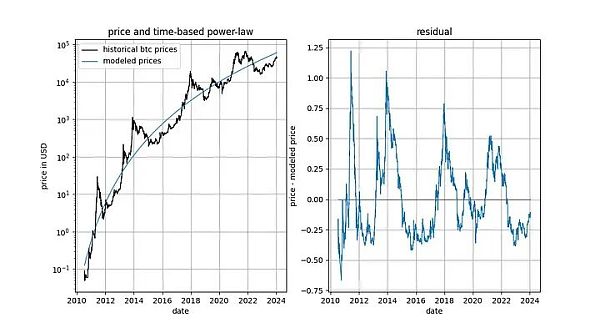
さらに、このモデルは優れた標本外パフォーマンスを示しています(下記参照)。スプリアス相関に基づくモデルは、単にスプリアス、すなわち正確な予測ができないだけであるべきです。標本外性能をテストする方法は、限られた量のデータ(ある日付まで)にモデルをフィットさせ、モデルがフィットしていない期間の予測(クロス・バリデーションに似ている)を行うことです。サンプル外の期間中、観測された価格はモデル化された価格と頻繁に交差し、観測された価格の最大偏差はモデル化された価格から系統的に遠ざかることはありません。
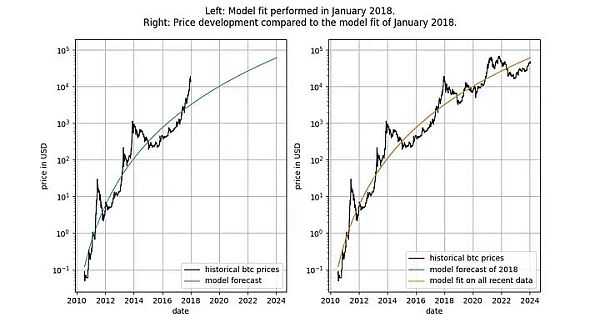
モデルが発表された後(2019年9月)には、より厳密にパフォーマンスを見ることができます。- 事後的にモデルを変更することはできないからだ。
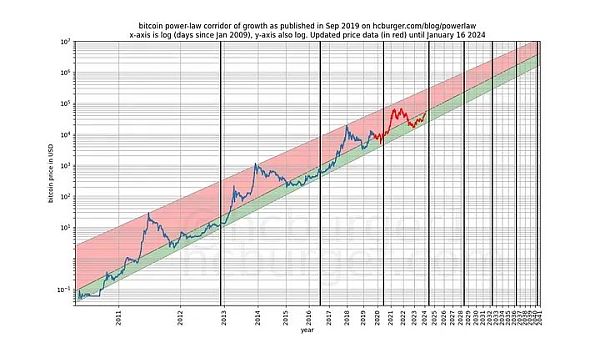
もし誰かが、モデルが偽の相関関係しか基づいていないと非難するなら、モデルの予測力はすでに疑われているはずだ。
log_timeとlog_priceの間でコインテグレーションが可能であるためには、2つの変数は同じ次数の確率変数でなければならず、少なくとも次数は1でなければなりません。
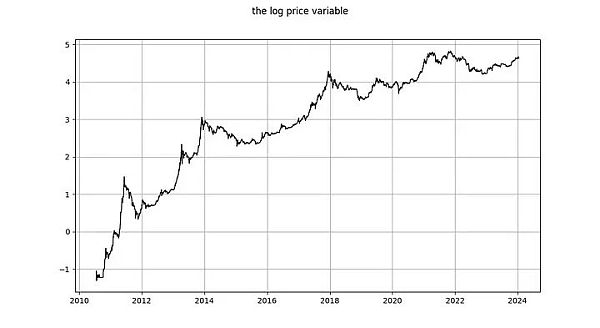
log_price は平滑化された時系列なのでしょうか。ADF検定(非定常性の検定)とKPSS検定(定常性の検定)を用いて、log(price)は疑いなく非定常であり、したがってI(1)以上であると結論付けています。したがって、非定常性をしっかりと棄却することはできず、対数価格に非定常性の兆候があると結論づけることはできない。"
独自の分析を行ってみましょう。Tim Stolteと同様に、異なる時間窓でADF検定を実行します:常に利用可能な最初の日付から開始し、各日に1日を追加します(日次データを使用します)。こうすることで、ADF検定の結果が時間とともにどのように変化するかを見ることができます。しかし、ティムやニックと違って、我々は実行するADF検定のバージョンを指定しなければならない。ウィキペディアによると、DF検定とADF検定には主に3つのタイプがあります:

これら3つのバージョンの違いは、異なるトレンドに対応(除去)できるということです。これはEngleとGrangerの決定論的トレンドを除去するという要件に関連しており、3つのバージョンは3つの単純なタイプの決定論的トレンドを除去することができます。最初のバージョンは、過去のlog_priceデータのみを使用して日々のlog_priceの変化を記述しようとします。2番目のバージョンは、定数項を使用することができ、その結果、log_priceは線形トレンド(上昇または下降)を持つことができる。3番目のバージョンは、2次(放物線)成分を許容します。
ティムとニックがどのバージョンを実行しているかはわかりませんが、3つとも実行してみます。
ADF検定で使用する最大ラグは1ですが、それ以上のラグを使用しても、結果と結論に有意な変化はありません。我々は、pythonのstatsmodels.tsa.stattools.adfuller関数を、"maxlag "を1、"regression "パラメータを "n"、"c"、"ct"(上記のWikipediaに記述されている3つのタイプに相当)で使用します。下の図では、検定によって返されたp値(統計的有意性の尺度)を示しており、p値が小さいほど平滑化の可能性が高いことを示しています(一般的に使われる閾値は0.05です)。
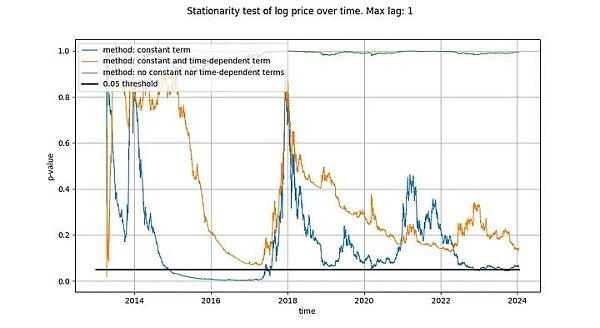
最初の方法(緑の線)は、log_priceの時系列が非平滑であると結論づけていることに注意してください。3番目のテスト(オレンジの線)も同じ結論に達しますが、決定的ではありません。興味深いことに、定数項を許容する検定(青い線)は、時系列が平滑かどうかを決定することができません(Timも定数項を持つADF検定を使っていると思われます)。なぜ3つのバージョンはこれほど違うのでしょうか?特になぜ定数項を使ったバージョンではlog_priceが平滑であることを除外できないのでしょうか?
説明はひとつしかありません。log_priceの差に定数項だけを使うと(log_priceに線形項が生じる)、時系列に「非常によく」適合し、その結果、(始点と終点からの乖離がかなり大きいにもかかわらず)ほとんど滑らかに見える残差シグナルが生じます。log_priceの決定論的傾向をまったく使わない、あるいは2次項の決定論的効果を使うことは、はるかに効果が低い。
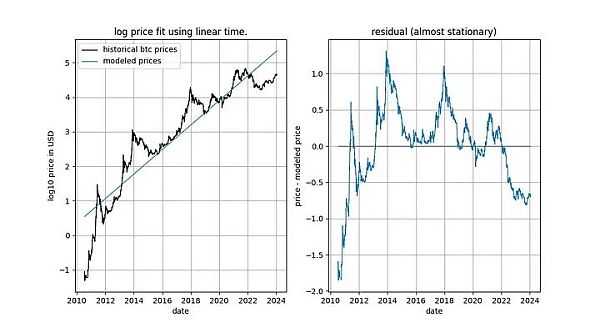
This already gives us a strong hint that there is a relationship between time and log_price.実際、定数項を使ったADF検定でシグナルが平滑であると結論づけられた場合、これは線形時間項がlog_priceを十分に近似し、平滑な残差が得られることを意味します。滑らかな残差を得ることは、スプリアスでない関係(すなわち、正しい説明変数が見つかったこと)のサインなので、望ましいことです。線形時間トレンドは、正確に我々が望むものではありませんが、我々はそれに近づいているようです。
私たちの結論は、(別の投稿で)次のように述べているMarcel Burger氏の結論とは著しく異なります:
「以前の分析で、私はビットコインの価格が一次積分であることを示しましたが、これは今でも有効です。ビットコインは、その価格の時間的な進化において、いかなる決定要因も示さない。"
我々は、線形時間はビットコインの価格の経時的な振る舞いを適切に説明できないと結論づけますが、log_priceが決定論的な時間的要因を持っていることは絶対に明らかです。また、(EngleとGrangerが要求するように)適切な決定論的要素を取り除いた後、log_priceがI(1)であることも明らかではありません。代わりに、トレンド平滑化されているように見えますが、適切な決定論的成分はまだ見つける必要があります。
もし私たちが共和分を探しているのであれば、log_priceがI(1)でないことはすでに問題です。なぜなら、2つの変数が共和分であるためには、両方ともI(1)以上でなければならないからです。
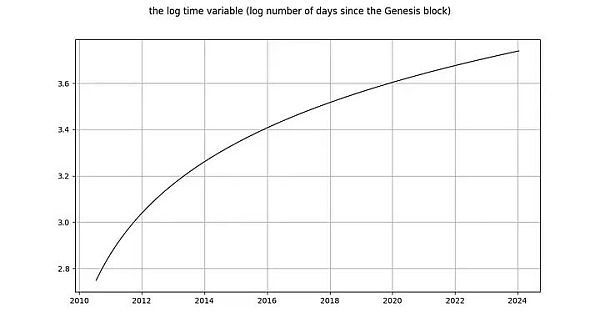
では、log_time変数を見てみましょう。Marcel Burgerは、log_timeは6次の積分を行うようだと結論付けています(数値的な問題にぶつかるまで、彼は差分を実行していました)。彼は、log_timeのような数学関数が、完全に決定論的な変数からランダム変数に変換されることを期待していますが、これは意味がありません。
ニックのlog_timeに関する結論は、log_price変数に関する結論と同じです:log_timeが非平滑であることは間違いなく、したがってI(1)以上です。これらの主張は驚くべきものである!積分次数と共分散は、決定論的傾向が排除された確率変数の概念を参照しています(上記のEngleとGranger [2]を参照)。注意:決定論的変数の値は事前に知られているが、確率変数の値は知られていない。時間は(明らかに)完全に決定論的であり、対数関数、したがってlog_timeもそうです。
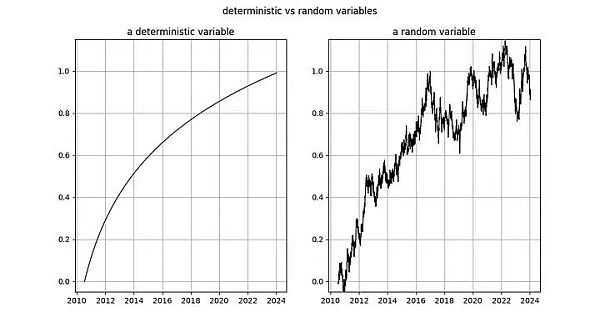
図のキャプション:左:ジェネシス・ブロック以来。からの日数の対数は完全に決定論的である。右:ランダム変数(左の決定論的変数と少し似ている)。
EngleとGrangerのアプローチに従い、log_timeから決定論的傾向を取り除くと、log(x) - log(x) = 0なので、残るのはゼロのベクトルだけです。完全に決定論的な変数であるlog_timeを確率変数に変換することができないので、EngleとGrangerのフレームワークを使うことができないのです。
完全に決定論的な変数がコインテグレーション分析でどのように問題になるかを見るもう一つの方法は、ディッキー・フラー検定のような平滑性検定がそれをどのように扱うかを考えることです。最も単純なケース(yが注目変数、rhoが推定される係数、uがホワイトノイズと仮定される誤差項)を考えてみましょう。誤差項u_{t}はすべてのt値に対して0です。なぜならランダムな要素がないからです。しかし、log_timeは時間の非線形関数なので、rhoの値も時間に依存しなければなりません。
ランダム変数の場合、変数rhoは以前のランダム値がどの程度記憶されているかを捉えるので、このモデルはより有用である。しかしランダムな値がない場合、このモデルは無意味です。
決定論的変数に対する他のタイプの検定でも同じ問題があります。
したがって、完全決定論的変数は、コインテグレーション分析の一部ではありません。別の言い方をすれば、決定論的なシグナルにはコインテグレーション分析は適用されず、シグナルの1つが決定論的であれば、コインテグレーション分析は偽の関係があると主張するための時代錯誤的なツールです。
共和分関係は、両方の変数がI(d)であり、dが少なくとも1に等しい場合にのみ存在します。log_timeは完全に決定論的な変数であり、静的検定では使えないことを示しました。log_timeがI(0)か、I(1)か、I(6)かはわかりません。また、log_priceはI(1)ではなく、トレンド平滑化されています。
log_timeとlog_priceの間には共和分(coointegration)がありませんが、これは時間ベースのべき乗則が統計的に無効であるか、スプリアスであることを意味するのでしょうか?
確かに
どのような適切な統計分析においても、決定論的変数とトレンド平滑化変数の混合を使用することは完全に正しいです。私たちの批評家たちが信じさせようとするように、共和分(cointegration)は統計的関係分析の中心点ではありません。
したがって、共和分分析は実行不可能である。しかし、べき乗モデルに適用される平滑化分析の場所はあるかもしれません。この問題をさらに掘り下げてみましょう。
入力変数の共和分分析から始めるのは、2つの変数の滑らかな線形結合を見つけたいからです。決定論的変数(log_time)と傾向平滑変数(log_price)を組み合わせて平滑変数を得ることは基本的に不可能です。したがって、厳密な意味での共和分(cointegration)を探す代わりに、(残差は2つの入力信号の単純な線形結合なので)残差について単純に平滑性検定を行うことができます。残差が滑らかであれば、Engle-Grangerの共和分検定(これが共和分である)に厳密に従わなかったとしても、滑らかな線形結合を見つけたことになります。
James G. MacKinnon [3]は、彼の論文 "Critical Values of Cointegration Tests "の中で、まさにこのように説明しています:もし "cointegration regression"(log_timeとlog_priceを関連づける回帰)が実行されれば、たとえEngle-Grangerのcointegration testに厳密に従わなかったとしても、(cointegrationの目的である)滑らかな線形結合を見つけることができます。もし「共和分回帰」(log_timeとlog_priceを結びつける回帰)が実行されたなら、共和分の検定(Engle-Granger検定)は、残差の平滑性の検定(DF検定またはADF検定)と同じものです。p>マッキノンは、もしlog_timeとlog_priceをつなぐパラメータが先験的に知られているならば、Engle-Grangerの連関検定は、残差の平滑化検定(DF検定またはADF検定)の3つの一般的なタイプのうちの1つを支持して、スキップすることができるという主張を繰り返しています:
そこで、結果の検定統計量以外は同じである2つの方法のどちらかを使うことができます:
1.log_timeをlog_priceにフィットさせ、残差(誤差)を計算する。残差からDFを計算するか、ADF検定を計算します。結果の統計量は、残差が平滑かどうかを示します。
ADF検定では、pythonのstatsmodels.tsa.stattools.adfuller関数を使い、Engle-Granger検定では、statsmodels.tsa.stattools.cointを使います。 どちらの関数でもというのは、残差は時間とともに一定のドリフトを含むべきではないからです(これは時間とともにモデルが価格を過大評価または過小評価し始めることを意味します)。
ADF検定とEngle-Granger検定は等価であると書きましたが、そうではありません。Engle-Grangerの連関検定はN=2の確率変数があると仮定していますが、ADF検定はN=1の確率変数があると仮定しています(Nは自由度の尺度です)。確率変数は、別の確率変数または決定論的変数に影響されうるが、決定論的変数は確率変数に影響されえない。したがって、我々のケース(決定論的変数log_timeが1つだけある)では、(N=1の確率変数を仮定する)ADF検定によって返される統計量が望ましいです。原理的には、Engle-Granger 検定とADF 検定は発散するかもしれませんが、時間ベースのモデルでは実際にはそうではありません。以下に示すように、結論は同じです:我々は残差の滑らかなベクトルを得ます。両方の検定のスコアは、臨界値0.05(残差が平滑であることを示す)をはるかに下回っており、長い間そうでした。
どちらの検定も、最初は滑らかな残差が正規であることを示していない。これは、残差信号の低周波数成分が非平滑信号と間違えられるためである。時間が経って初めて、残差の平均回帰が明らかになり、実際に滑らかになる。
S2Fモデルは一般的に否定されてきましたが、それは厳密な意味での共和分(cointegration)が不可能であるためと思われます。しかし、このモデルは非常に滑らかに見える残差を生成します。
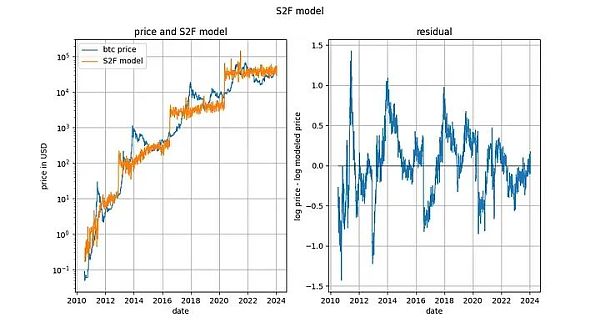
実際、Engle-Granger共同継起検定とADF安定性検定(決定論的変数とランダム変数が存在するため望ましい)の両方が、ゼロに非常に近いp値をもたらします。したがって、S2Fモデルは「共和分の欠如」(実際には「平滑性の欠如」)に基づいて除外されるべきではない。
しかし、2020年初頭に指摘したように、S2Fモデルが有効でないことを示す兆候は他にもあります。BTCUSDの価格がS2Fモデルの予測よりも低くなるという私たちの予測は、先見の明があったことが証明されました。
長期的な株価指数を時間に対して見るのも興味深い(この場合は配当再投資なしのS&P500)。主要な株式市場の株価指数が平均約7%の指数関数的な速度で成長することはよく知られています。実際、私たちは指数回帰でこれを確認している。
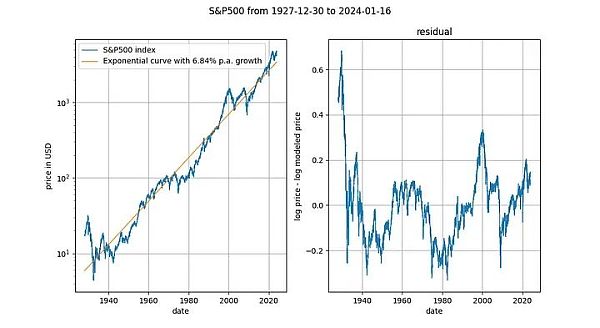
ここで、もう1つの決定論的変数(時間)に遭遇します。 Engle-Grangerの共同継起検定では約0.025のp値が得られ、ADF検定(好ましい)では約0.0075のp値が得られます。値は約0.0075です(しかし、これらの値は選択された正確な期間に大きく依存します)。もう一度、残差は平滑である。株価の指数的な時間トレンドは有効です。
S2Fモデルは当初、(特にマルセル・バーガーとニック・エンブローによって)高く評価されました。しかし、潮目が変わると、S2Fモデルは厳密な意味での共和分関係を持たないことが明らかになり、マルセルもニックもS2Fモデルの無効を宣言し、船出した。この出来事の後、S2Fモデルに対する一般的な見方は変わったようで、エリック・ウォールが出来事の推移を見事に短くまとめています。
私たちは説明しましたし、計量経済学の文献(MacKinnon [3])も私たちに同意しています。この考え方に沿って、我々はS2Fモデルについて、共和分/平滑性の観点からは何の問題もないと考えており、したがって、共和分の欠如が疑われるからといって、S2Fモデルに対する我々の見方を変えるのは間違っている。私たちはS2Fモデルが間違っていることに同意しますが、それはコインテグレーションの欠如以外の理由で間違っているのです。
ビットコインの時間のべき乗モデルは、log_timeとlog_priceの関係が偽であるとされる、共和分(coointegration)の欠如を批判されています。私たちは、ビットコインの時間ベースのべき乗モデルの残差は明らかに滑らかであることを示しました。
ビットコインの時間ベースのべき乗モデルは有効で、安定しており、頑健です。いつものように。
参考文献
1. "Universal Cointegration and Its Applications" Tu et al.補足情報
2. "Co-Integration and Error Correction: Representation, Estimation, and Testing" Tu et al.
3.(訳注:この本は、「邦訳」(講談社現代新書)に収録されています。
AIのコミュニティは、その将来と神を創造するのに十分な大きさかどうかをめぐる教義上の争いに巻き込まれている。
 JinseFinance
JinseFinance次の相場(来年まで)で、ビットコインの価格が著しく割高になった場合、4年周期の法則は少なくとももう1回続くと私は考えている。
 JinseFinance
JinseFinanceビットコインは普通の資産というより自然現象に近い。ビットコインは金融資産というより、都市や生物に近い。
 JinseFinance
JinseFinance秋にBTCへの信頼が強まった人だけが、割引BTCを保有する資格を得ることができる。
 JinseFinance
JinseFinanceエヌビディアの共同創業者兼CEOであるJen-Hsun Huangは、Computex 2024(台北国際コンピュータ見本市)で基調講演を行い、人工知能の時代がいかに新たな世界的産業革命を促進するかを語った。
 JinseFinance
JinseFinanceTechchainはまず、パワー・ロー・モデルの著者であるジョバンニ・サントスターシによる最近の記事『The Bitcoin Power Law Theory』を読者に紹介し、このトピックをさらに深く掘り下げるための基礎とする。
 JinseFinance
JinseFinanceビットコインのエコシステムにおける業界の現状、Bitcoin Magazineが提案するLayer2の定義についての考え、そしてビットコインのLayer2をどのように判断するかについてのあなた自身の考え。
 JinseFinance
JinseFinanceビットコインの時間ベースのべき乗則モデルは、これまでと同様に有効で、安定しており、強力である。
 JinseFinance
JinseFinance新たな半減サイクルが終わりに近づくにつれ、私たちは何を期待すべきなのだろうか?
 JinseFinance
JinseFinanceポルトガルで建設中のビットコイン ホステルは、デジタル通貨以上のものを念頭に置いて構築されたビジネスの成長傾向を反映しています。
 Cointelegraph
Cointelegraph